Difference between revisions of "Aufgaben:Exercise 2.14: Petersen Algorithm?"
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding}} | {{quiz-Header|Buchseite=Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding}} | ||
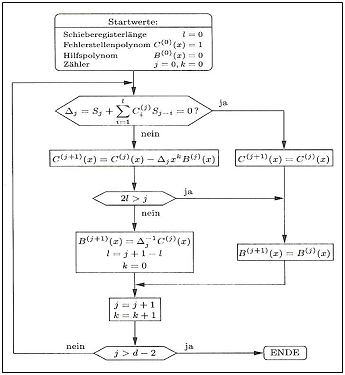
| − | [[File: P_ID2580__KC_A_2_14_v1.png|right|frame| | + | [[File: P_ID2580__KC_A_2_14_v1.png|right|frame|Chart from [Bos98]: <br>'''(1)''' Fast decoding algorithm for RS codes. <br>'''(2)''' It is therefore not the Petersen algorithm!]] |
| − | In the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding|"Error | + | In the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding|"Error Correction According to Reed-Solomon Coding"]] the decoding of Reed–Solomon codes with the "Petersen algorithm" was treated. |
* Its advantage is that the individual steps are traceable. | * Its advantage is that the individual steps are traceable. | ||
| Line 17: | Line 17: | ||
Hints: | Hints: | ||
| − | * The exercise belongs to the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding| "Error | + | * The exercise belongs to the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding| "Error Correction According to Reed-Solomon Coding"]]. |
| − | * The diagram shows the flowchart of one of the most popular methods for decoding Reed–Solomon codes. Which algorithm | + | |
| − | *The graphic was taken from the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998". We thank the author Martin Bossert for the permission to use the graphic. | + | * The diagram shows the flowchart of one of the most popular methods for decoding Reed–Solomon codes. Which algorithm is mentioned in the sample solution to this exercise. |
| + | |||
| + | *The graphic was taken from the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998". We thank the author Martin Bossert for the permission to use the graphic. | ||
| Line 33: | Line 35: | ||
{What is most complex in the Petersen algorithm? | {What is most complex in the Petersen algorithm? | ||
|type="()"} | |type="()"} | ||
| − | - Checking if there are (one or more) errors at all, | + | - Checking if there are $($one or more$)$ errors at all, |
+ the localization of the errors, | + the localization of the errors, | ||
- the determination of the error value. | - the determination of the error value. | ||
Revision as of 14:16, 31 October 2022
In the chapter "Error Correction According to Reed-Solomon Coding" the decoding of Reed–Solomon codes with the "Petersen algorithm" was treated.
- Its advantage is that the individual steps are traceable.
- Very much of disadvantage is however the immensely high decoding expenditure.
Already since the invention of Reed–Solomon coding in 1960, many scientists and engineers were engaged in the development of algorithms for Reed–Solomon decoding as fast as possible, and even today "Algebraic Decoding" is still a highly topical field of research.
In this exercise, some related concepts will be explained. A detailed explanation of these procedures has been omitted in our "$\rm LNTwww $".
Hints:
- The exercise belongs to the chapter "Error Correction According to Reed-Solomon Coding".
- The diagram shows the flowchart of one of the most popular methods for decoding Reed–Solomon codes. Which algorithm is mentioned in the sample solution to this exercise.
- The graphic was taken from the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998". We thank the author Martin Bossert for the permission to use the graphic.
Questions
Solution
- In principle, a syndrome decoder would also be possible with RS codes, but with the large codeword lengths $n$ common here, extremely long decoding times would result.
- For convolutional codes (these work serially) syndrome decoding makes no sense at all.
(2) As can be seen from the discussion in the theory section, error localization involves by far the greatest effort ⇒ Answer 2.
(3) Correct answers 1, 3, and 4:
- These procedures are summarized on the "Fast Reed–Solomon decoding" page.
- The BCJR– and Viterbi algorithms, on the other hand, refer to "Decoding of convolutional codes".
- The graphic on the information page shows the Berlekamp–Massey algorithm (BMA).
- The explanation of this figure can be found in the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998" from page 73.