Aufgaben:Exercise 4.13: Decoding LDPC Codes

• Return to book

Given LDPC parity-check matrix

The exercise deals with  "Iterative decoding of LDPC–codes"  according to the  Message passing algorithm.

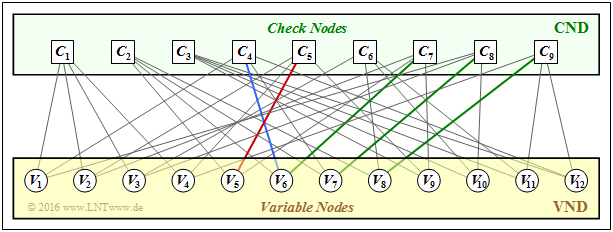
The starting point is the presented  $9 × 12$–parity-check matrix  $\mathbf{H}$, which is to be represented as a Tanner–graph at the beginning of the exercise. It should be noted that:

• The  variable nodes  (abbreviated  $\rm VNs$)  $V_i$  denote the  $n$  codeword bits.
• The  check nodes  (abbreviated  $\rm CNs$)  $C_j$  represent the  $m$  parity-check equations.
• A connection between  $V_i$  and  $C_j$  indicates that the matrix element  $h_{j,\hspace{0.05cm} i}$  of the parity-check matrix  $\mathbf{H}$  $($in row  $j$, column  $i)$  is equal  $1$ . For  $h_{j,\hspace{0.05cm}i} = 0$  there is no connection between  $V_i$  and  $C_j$.
• The  neighbors  $N(V_i)$  of  $V_i$  is called the set of all  check nodes  $C_j$ connected to  $V_i$  in the Tanner ;graph. Correspondingly, to  $N(C_j)$  belong all variable nodes  $V_i$  with a connection to  $C_j$.

The decoding is performed alternately with respect to

• den  variable nodes   ⇒   variable nodes decoder (VND), and
• the  check nodes   ⇒   check nodes decoder (CND).

This is referred to in subtasks (5) and (6)'.

Hints:

• The exercise belongs to the chapter  "Basic information about Low–density Parity–check Codes".
• Reference is made in particular to the page  "Iterative decoding of LDPC codes".

Questions

1

How many  variable nodes $(I_{\rm VN})$  and  check nodes $(I_{\rm CN})$  are to be considered?

$I_{\rm VN} \ = \ $

$I_{\rm CN} \ = \ $

2

Which of the following  check nodes  and  variable nodes  are connected?

	$C_4$  and  $V_6$.
	$C_5$  and  $V_5$.
	$C_6$  and  $V_4$.
	$C_6$  and  $V_i$  for  $i > 9$.
	$C_j$  and  $V_{j-1}$  for  $j > 6$.

3

Which statements are true regarding neighbors  $N(V_i)$  and  $N(C_j)$ ?

	$N(V_1) = \{C_1, \ C_2, \ C_3, \ C_4\}$,
	$N(C_1) = \{V_1, \ V_2, \ V_3, \ V_4\}$,
	$N(V_9) = \{C_3, \ C_5, \, C_7\}$,
	$N(C_9) = \{V_3, \ V_5, \ V_7\}$.

4

Which statements are true for the  variable node decoder  (VND)?

	At the beginning (iteration 0) the  $L$ values of the nodes  $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \ V_n$  corresponding to the channel input values  $y_i$  preassigned.
	For the VND represents  $L(C_j → V_i)$  apriori–information.
	There are analogies between the  variable node decoder  and the decoding of a single parity–check code.

5

Which statements are true for the  check node decoder  (CND)?

	The CND returns the desired a posteriori–$L$–values at the end.
	For the CND represents  $L(C_j → V_i)$  apriori–information.
	There are analogies between the  check node decoder  and the decoding of a single parity–check code.

Solution

Solution

(1)  The variable node$\rm (VN)$ $V_i$ stands for the $i$–th codeword bit, so that $I_{\rm VN}$ is equal to the codeword length $n$.

• From the column number of the $\mathbf{H}$–matrix, we can see $I_{\rm VN} = n \ \underline{= 12}$.
• For the set of all variable nodes,one can thus write in general: ${\rm VN} = \{V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , V_i, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_n\}$.
• The check node ${\rm (CN)} \ C_j$ represents the $j$ parity-check equation, and for the set of all check nodes, ${\rm CN} = \{C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_j, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_m\}$.
• From the number of rows of the $\mathbf{H}$ matrix we get $I_{\rm CN} \ \underline {= m = 9}$.

(2)  The results can be read from the Tanner graph sketched below.

Tanner graph for the present example.

Correct are the proposed solutions 1, 2 and 5:

• The matrix element $h_{5,\hspace{0.05cm}5}$ (column 5, row 5) ist $1$  
  ⇒   red edge.
• The matrix element $h_{4,\hspace{0.05cm} 6}$ (column 4, row 6) ist $1$  
  ⇒   blue edge.
• The matrix element $h_{6, \hspace{0.05cm}4}$ (column 6, row 4) ist $0$  
  ⇒   no edge.
• $h_{6,\hspace{0.05cm} 10} = h_{6,\hspace{0.05cm} 11} = 1$. But $h_{6,\hspace{0.05cm}12} = 0$  
  ⇒   not all three edges exist.
• It holds $h_{7,\hspace{0.05cm}6} = h_{8,\hspace{0.05cm}7} = h_{9,\hspace{0.05cm}8} = 1$   ⇒   green edges.

(3)  It is a regular LDPC code with

• $w_{\rm Z}(j) = 4 = w_{\rm Z}$ für $1 ≤ j ≤ 9$,
• $w_{\rm S}(i) = 3 = w_{\rm S}$ für $1 ≤ i ≤ 12$.

The answers 2 and 3 are correct, as can be seen from the first row and ninth column, respectively, of the parity-check matrix $\mathbf{H}$.
The Tanner graph confirms these results:

• From $C_1$ there are edges to $V_1, \ V_2, \ V_3$, and $V_4$.
• From $V_9$ there are edges to $C_3, \ C_5$, and $C_7$.

The answers 1 and 4 cannot be correct already because

• the neighborhood $N(V_i)$ of each variable node $V_i$ contains exactly $w_{\rm S} = 3$ elements, and
• the neighborhood $N(C_j)$ of each check ndes $C_j$ contains exactly $w_{\rm Z} = 4$ elements.

(4)  Correct are proposed solutions 1 and 2, as can be seen from the "corresponding theory page":

• At the beginning of decoding  $($so to speak at iteration $I=0)$  the $L$–values of the variable nodes  ⇒  $L(V_i)$ are preallocated with the channel input values.
• Later  $($from iteration $I = 1)$  the log–likelihood–ratio $L(C_j → V_i)$ transmitted by the CND is considered in the VND as a priori information.
• Answer 3 is wrong. Rather, the correct answer would be: there are analogies between the VND algorithm and the decoding of a repetition code.

(5)  Correct is only proposed solution 3 because.

• the final a posteriori $L$ values are derived from the VND, not from the CND,
• the $L$ value $L(C_j → V_i)$ represents extrinsic information for the CND, and
• there are indeed analogies between the CND–algorithm and SPC–decoding.