Difference between revisions of "Theory of Stochastic Signals/Power-Spectral Density"
| Line 62: | Line 62: | ||
Die Interpretation dieser Grafiken erfolgt im nächsten Abschnitt. | Die Interpretation dieser Grafiken erfolgt im nächsten Abschnitt. | ||
| + | |||
| + | ==Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite (2)== | ||
| + | Anhand der Grafiken auf der letzten Seite sind folgende Aussagen möglich: | ||
| + | *Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse besitzen gleiche Leistung: | ||
| + | $${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{\Phi_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{\Phi_y(f)} \hspace{0.1cm} {\rm d} f .$$ | ||
| + | *Das aus der klassischen (deterministischen) Systemtheorie bekannte Reziprozitätsgesetz von Zeitdauer und Bandbreite gilt hier ebenfalls: Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt. | ||
| + | *Als Beschreibungsgröße verwenden wir hier die äquivalente LDS-Bandbreite $∇f$ (man spricht ''Nabla-f''), ähnlich definiert wie die äquivalente AKF-Dauer $∇τ$ in Kapitel 4.4: | ||
| + | $${{\rm \nabla} f_x} = \frac {1}{\Phi_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{\Phi_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$ | ||
| + | *Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang: | ||
| + | $${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} | ||
| + | {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$ | ||
| + | |||
| + | |||
| + | {{Beispiel}} | ||
| + | Wir gehen wieder von der Grafik auf der letzten Seite aus: | ||
| + | *Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x =$ 0.33 μs und $∇f_x =$ 3 MHz. | ||
| + | *Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y =$ 1 μs. | ||
| + | *Die äquivalente LDS-Bandbreite beträgt somit nur mehr $∇f_y = ∇f_x/3 =$ 1 MHz. | ||
| + | |||
| + | |||
| + | {{end}} | ||
| + | |||
| + | |||
| + | {{Box}} | ||
| + | '''Beweis:''' Entsprechend den obigen Definitionen gilt: | ||
| + | $${{\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac {\Phi_x(f = {\rm 0)}}{ \varphi_x(\tau = \rm 0)},$$ | ||
| + | $${{\rm \nabla} f_x} = \frac {1}{ \Phi_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{\Phi_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)}}{\Phi_x(f = \rm 0)}.$$ | ||
| + | ⇒ Das Produkt aus äquivalenter AKF-Dauer und äquivalenter LDS-Bandbreite ist gleich 1. | ||
| + | {{end}} | ||
| + | |||
| + | |||
| + | Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte Weiße Rauschen dar. Dieses beinhaltet alle Spektralanteile (bis ins Unendliche) und die äquivalente LDS-Bandbreite $∇f$ ist unendlich groß. Das hier angegebene Gesetz besagt dann, dass damit für die äquivalente AKF-Dauer $∇τ =$ 0 gelten muss; die AKF des weißen Rauschens ist diracförmig. | ||
| + | |||
| + | Mehr zu dieser Thematik finden Sie in den nachfolgenden Lernvideos, insbesondere im Teil 2: | ||
| + | |||
| + | Der AWGN-Kanal – Teil 1 (Dauer 6:00) | ||
| + | Der AWGN-Kanal – Teil 2 (Dauer 5:15) | ||
| + | Der AWGN-Kanal – Teil 3 (Dauer 6:15) | ||
| + | |||
| + | |||
Revision as of 18:44, 5 June 2016
Contents
Theorem von Wiener-Chintchine
Im Weiteren beschränken wir uns auf ergodische Prozesse. Wie im Kapitel 4.4 gezeigt wurde, gelten dann die folgenden Aussagen:
- Jede einzelne Musterfunktion $x_i(t)$ ist repräsentativ für den gesamten Zufallsprozess { $x_i(t)$}. Alle Zeitmittelwerte sind somit identisch mit den dazugehörigen Scharmittelwerten.
- Die Autokorrelationsfunktion, die allgemein von den beiden Zeitparametern $t_1$ und $t_2$ beeinflusst wird, hängt nur noch von der Zeitdifferenz $τ = t_2 – t_1$ ab:
$$\varphi_x(t_1,t_2)={\rm E}[x(t_{\rm 1})\cdot x(t_{\rm 2})] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$
Diese Funktion liefert quantitative Aussagen über die (linearen) statistischen Bindungen innerhalb des ergodischen Prozesses { $x_i(t)$} im Zeitbereich. Die äquivalente Beschreibungsgröße im Frequenzbereich ist die spektrale Leistungsdichte, häufig auch als Leistungsdichtespektrum (LDS) bezeichnet.
Das Leistungsdichtespektrum (LDS) eines ergodischen Zufallsprozesses { $x_i(t)$} ist die Fouriertransformierte der Autokorrelationsfunktion (AKF): $${\Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\pi} f \tau} {\rm d} \tau. $$ Diesen Funktionalzusammenhang nennt man das Theorem von Wiener und Chintchine.
Ebenso kann die AKF als Fourierrücktransformierte des LDS berechnet werden (siehe Kapitel 3.1 des Buches „Signaldarstellung”):
$$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} \Phi_x(f) \cdot {\rm e}^{{\rm j\pi} f \tau} {\rm d} f.$$
Die beiden Gleichungen sind nur dann direkt anwendbar, wenn der Zufallsprozess weder einen Gleichanteil noch periodische Anteile beinhaltet. Andernfalls muss man nach den Angaben auf Seite 4 dieses Abschnitts vorgehen: Spektrale Leistungsdichte mit Gleichsignalkomponente.
Physikalische Interpretation und Messung
Das folgende Bild zeigt eine Anordnung zur (näherungsweisen) messtechnischen Bestimmung des Leistungsdichtespektrums $Φ_x(f)$.
Hierzu ist folgendes anzumerken:
- Das Zufallssignal $x(t)$ wird auf ein (möglichst) rechteckförmiges und (möglichst) schmalbandiges Filter mit Mittenfrequenz $f$ und Bandbreite $Δf$ gegeben, wobei $Δf$ entsprechend der gewünschten Frequenzauflösung hinreichend klein gewählt werden muss.
- Das entsprechende Ausgangssignal $x_f(t)$ wird quadriert und anschließend der Mittelwert über eine hinreichend lange Messdauer $T_{\rm M}$ gebildet. Damit erhält man die Leistung von $x_f(t)$ bzw. die Leistungsanteile von $x(t)$ im Spektralbereich von $f – Δf/2$ bis $f + Δf/2$:
$$P_{xf} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f(t)^2 \hspace{0.1cm}\rm d \it t.$$
- Die Division durch $Δf$ führt von der spektralen Leistung zur spektralen Leistungsdichte:
$${\Phi_{x \rm +}}(f) =\frac{P_{xf}}{{\rm \Delta} f} \hspace {0.5cm} {\rm bzw.} \hspace {0.5cm} \Phi_{x}(f) = \frac{P_{xf}}{{\rm 2 \cdot \Delta} f}.$$
- Hierbei bezeichnet $Φ_{x+}(f) = 2 · Φ_x(f)$ das einseitige, nur für positive Frequenzen definierte LDS. Für negative Frequenzen ist $Φ_{x+}(f) =$ 0. Im Gegensatz dazu gilt für das üblicherweise verwendete zweiseitige LDS: $Φ_x(–f) = Φ_x(f)$.
- Während die Leistung $P_{xf}$ mit kleiner werdender Bandbreite $Δf$ gegen Null tendiert, bleibt die spektrale Leistungsdichte ab einem hinreichend kleinen Wert von $Δf$ nahezu konstant.
- Für die exakte Bestimmung von $Φ_x(f)$ sind zwei Grenzübergänge notwendig:
$${\Phi_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$
Aus dieser physikalischen Interpretation folgt weiter, dass das LDS stets reell ist und nie negativ werden kann. Die gesamte Signalleistung von $x(t)$ erhält man dann durch Integration über alle Spektralanteile:
$$P_x = \int^{\infty}_{0}\Phi_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}\Phi_x(f)\hspace{0.1cm} {\rm d} f .$$
Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite (1)
Alle Gesetzmäßigkeiten der Fouriertransformation, hergeleitet im Kapitel 3.2 des Buches „Signaldarstellung” für deterministische Signale, können auch auf die Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) eines Zufallsprozesses angewendet werden. Aufgrund der spezifischen Eigenschaften von AKF (stets reell und gerade) und LDS (stets reell, gerade und nicht-negativ) liefern allerdings nicht alle Gesetze sinnvolle Ergebnisse.
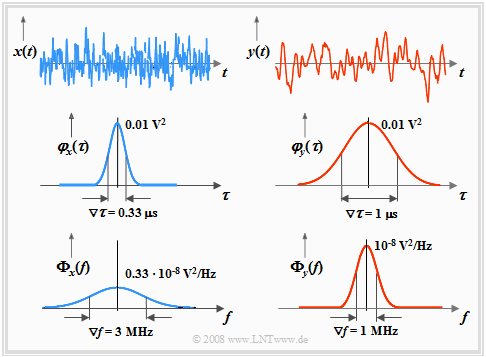
Wir betrachten nun wie auf der Seite Interpretation der Autokorrelationsfunktion im Kapitel 4.4 zwei unterschiedliche ergodische Zufallsprozesse { $x_i(t)$} und { $y_i(t)$} anhand
- der beiden Mustersignale $x(t)$ bzw. $y(t)$ ⇒ obere Skizze,
- der beiden Autokorrelationsfunktionen $φ_x(τ)$ bzw. $φ_y(τ)$ ⇒ mittlere Skizze,
- der beiden Leistungsdichtespektren $Φ_x(f)$ bzw. $Φ_y(f)$ ⇒ untere Skizze.
Die Interpretation dieser Grafiken erfolgt im nächsten Abschnitt.
Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite (2)
Anhand der Grafiken auf der letzten Seite sind folgende Aussagen möglich:
- Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse besitzen gleiche Leistung:
$${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{\Phi_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{\Phi_y(f)} \hspace{0.1cm} {\rm d} f .$$
- Das aus der klassischen (deterministischen) Systemtheorie bekannte Reziprozitätsgesetz von Zeitdauer und Bandbreite gilt hier ebenfalls: Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt.
- Als Beschreibungsgröße verwenden wir hier die äquivalente LDS-Bandbreite $∇f$ (man spricht Nabla-f), ähnlich definiert wie die äquivalente AKF-Dauer $∇τ$ in Kapitel 4.4:
$${{\rm \nabla} f_x} = \frac {1}{\Phi_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{\Phi_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$
- Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang:
$${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$
Wir gehen wieder von der Grafik auf der letzten Seite aus:
- Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x =$ 0.33 μs und $∇f_x =$ 3 MHz.
- Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y =$ 1 μs.
- Die äquivalente LDS-Bandbreite beträgt somit nur mehr $∇f_y = ∇f_x/3 =$ 1 MHz.
Beweis: Entsprechend den obigen Definitionen gilt: $${{\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac {\Phi_x(f = {\rm 0)}}{ \varphi_x(\tau = \rm 0)},$$ $${{\rm \nabla} f_x} = \frac {1}{ \Phi_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{\Phi_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)}}{\Phi_x(f = \rm 0)}.$$ ⇒ Das Produkt aus äquivalenter AKF-Dauer und äquivalenter LDS-Bandbreite ist gleich 1.
Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte Weiße Rauschen dar. Dieses beinhaltet alle Spektralanteile (bis ins Unendliche) und die äquivalente LDS-Bandbreite $∇f$ ist unendlich groß. Das hier angegebene Gesetz besagt dann, dass damit für die äquivalente AKF-Dauer $∇τ =$ 0 gelten muss; die AKF des weißen Rauschens ist diracförmig.
Mehr zu dieser Thematik finden Sie in den nachfolgenden Lernvideos, insbesondere im Teil 2:
Der AWGN-Kanal – Teil 1 (Dauer 6:00) Der AWGN-Kanal – Teil 2 (Dauer 5:15) Der AWGN-Kanal – Teil 3 (Dauer 6:15)