Difference between revisions of "Modulation Methods/Pulse Code Modulation"
| Line 137: | Line 137: | ||
*Bei natürlicher Abtastung kann zur Signalrekonstruktion wie bei der idealen Abtastung (mit einem Diracpuls) ein idealer rechteckförmiger Tiefpass verwendet werden. | *Bei natürlicher Abtastung kann zur Signalrekonstruktion wie bei der idealen Abtastung (mit einem Diracpuls) ein idealer rechteckförmiger Tiefpass verwendet werden. | ||
*Allerdings muss zur Amplitudenanpassung im Durchlassbereich eine Verstärkung um den Faktor $T_{\rm A}/T_{\rm R}$ berücksichtigt werden. | *Allerdings muss zur Amplitudenanpassung im Durchlassbereich eine Verstärkung um den Faktor $T_{\rm A}/T_{\rm R}$ berücksichtigt werden. | ||
| + | |||
| + | ==Natürliche und diskrete Abtastung (3)== | ||
| + | Bei der diskreten Abtastung erfolgt – zumindest gedanklich – zunächst die Multiplikation des Diracpulses $p_δ(t)$ mit dem Quellensignal $q(t)$ und erst danach die Faltung mit dem Rechteckimpuls $g_{\rm R}(t)$: | ||
| + | $$q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) | ||
| + | \cdot q(t)\right ]\star g_{\rm R}(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \star Q(f) \right ] \cdot G_{\rm R}(f)/{T_{\rm A}} \hspace{0.05cm}.$$ | ||
| + | Es ist unerheblich, aber durchaus zweckmäßig, dass hier der Faktor $1/T_{\rm A}$ zur Bewertungsfunktion $G_{\rm R}(f)$ hinzugefügt wurde. Damit gilt wieder $G_{\rm R}(f)/T_{\rm A} = T_{\rm R}/T_{\rm A} · {\rm si}(πfT_{\rm R}).$ | ||
| + | |||
| + | |||
| + | [[File: P_ID1596__Mod_T_4_1_S3c_neu.png | Spektrum bei diskreter Abtastung]] | ||
| + | |||
| + | |||
| + | Die obere Grafik zeigt die Spektralfunktion $P_δ(f) \star Q(f)$ nach idealer Abtastung. Bei diskreter Abtastung mit einem Rechteckpuls ergibt sich dagegen das Spektrum $Q_{\rm A}(f)$ entsprechend dem unteren Diagramm. Man erkennt: | ||
| + | *Jedes der unendlich vielen Teilspektren hat nun eine andere Form. Wichtig ist allerdings nur das Spektrum mit der Mitte bei der Frequenz $f =$ 0, da alle anderen Spektralanteile empfängerseitig durch den Tiefpass der Signalrekonstruktion entfernt werden. | ||
| + | *Verwendet man für diesen Tiefpass wieder ein Rechteckfilter mit der Verstärkung um $T_{\rm A}/T_{\rm R}$ im Durchlassbereich, so erhält man für das Ausgangsspektrum: | ||
| + | $$V(f) = Q(f) \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.05cm}.$$ | ||
| + | *Das bedeutet: Bei diskreter Abtastung und Rechteckfilterung kommt es zu Dämpfungsverzerrungen entsprechend der Bewertungsfunktion ${\rm si}(πfT_{\rm R})$. Diese sind um so stärker, je größer $T_{\rm R}$ ist. Nur im Grenzfall $T_{\rm R} → 0$ gilt ${\rm si}(πfT_{\rm R}) =$ 1. | ||
| + | *Allerdings können durch eine ideale Entzerrung diese linearen Dämpfungsverzerrungen vollständig kompensiert werden. Mit | ||
| + | $$H(f) = \left\{ \begin{array}{l} (T_{\rm A}/T_{\rm R})/{\rm si}(\pi f T_{\rm R}) \\ 0 \\ \end{array} \right.\quad\begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} | ||
| + | {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ | ||
| + | {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2} \\ | ||
| + | \end{array}$$ | ||
| + | :erhält man $V(f) = Q(f)$ bzw. $υ(t) = q(t)$. | ||
| + | |||
Revision as of 18:05, 20 June 2016
Contents
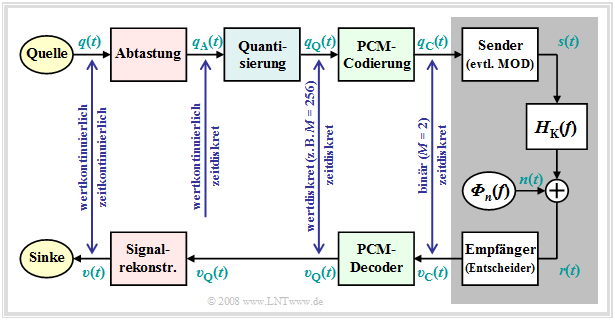
Prinzip und Blockschaltbild (1)
Nahezu alle heute eingesetzten Modulationsverfahren arbeiten digital. Deren Vorteile wurden schon im Kapitel 1.1 aufgeführt. Das erste Konzept zur digitalen Signalübertragung wurde bereits 1938 von Alec Reeves entwickelt und wird seit den 1960er Jahren unter dem Namen Pulscodemodulation (PCM) auch in der Praxis eingesetzt. Auch wenn sich viele der in den letzten Jahren konzipierten digitalen Modulationsverfahren von der PCM im Detail unterscheiden, so eignet sich diese doch sehr gut, um das Prinzip all dieser Verfahren zu erklären.
Die Aufgabe des PCM–Systems ist es,
- das analoge Quellensignal $q(t)$ in das Binärsignal $q_{\rm C}(t)$ umzusetzen – diesen Vorgang bezeichnet man auch als A/D–Wandlung,
- dieses Signal über den Kanal zu übertragen, wobei das empfängerseitige Signal $υ_{\rm C}(t)$ wegen des Entscheiders ebenfalls binär ist,
- schließlich aus dem Binärsignal $υ_{\rm C}(t)$ das analoge, wert– und zeitkontinuierliche Sinkensignal $υ(t)$ zu rekonstruieren ⇒ D/A–Wandlung.
Prinzip und Blockschaltbild (2)
Weiterhin ist zum obigen PCM–Blockschaltbild anzumerken:
- Der PCM–Sender (bzw. der A/D–Wandler) setzt sich aus den drei Funktionsblöcken Abtastung – Quantisierung – PCM–Codierung zusammen, die in den nächsten Abschnitten noch im Detail beschrieben werden.
- Der grau hinterlegte Block zeigt das digitale Übertragungssystem mit digitalem Sender und Empfänger (letzterer beinhaltet auch einen Entscheider), sowie dem analogen Übertragungskanal, gekennzeichnet durch den Frequenzgang $H_{\rm K}(f)$ und die Rauschleistungsdichte ${\it Φ}_n(f)$.
- Dieser Block wird in den ersten drei Kapiteln des Buches „Digitalsignalübertragung” eingehend behandelt. Im Kapitel 5 des gleichen Buches finden Sie auch digitale Kanalmodelle, die das Übertragungsverhalten anhand der Binärsignale $q_{\rm C}(t)$ und $υ_{\rm C}(t)$ phänomenologisch beschreiben.
- Weiter erkennt man aus dem Blockschaltbild, dass es für die Quantisierung empfängerseitig keine Entsprechung gibt. Deshalb wird sich auch bei fehlerfreier Übertragung, also für $υ_{\rm C}(t) = q_{\rm C}(t)$, das analoge Sinkensignal $υ(t)$ vom Quellensignal $q(t)$ unterscheiden.
- Als Maß für die Qualität des (digitalen) Übertragungssystems verwenden wir das Sinken–SNR als der Quotient der Leistungen von Nutzsignal $q(t)$ und Fehlersignal $ε(t) = υ(t) – q(t)$:
$$\rho_{v} = \frac{P_q}{P_\varepsilon}\hspace{0.3cm} {\rm mit}\hspace{0.3cm}P_q = \overline{q(t)^2}, \hspace{0.2cm}P_\varepsilon = \overline{[v(t) - q(t)]^2}\hspace{0.05cm}.$$
- Hierbei ist ideale Amplitudenanpassung vorausgesetzt, so dass im Idealfall (das heißt: Abtastung gemäß dem Abtasttheorem, bestmögliche Signalrekonstruktion, unendlich feine Quantisierung) das Sinkensignal $υ(t)$ mit dem Quellensignal $q(t)$ exakt übereinstimmen würde.
Wir möchten Sie bereits hier auf das 3–teilige Lernvideo Pulscodemodulation (Gesamtdauer 46:45) hinweisen, dass alle Aspekte der PCM beinhaltet. Das Prinzip wird im ersten Teil ausführlich erläutert.
Abtastung und Signalrekonstruktion (1)
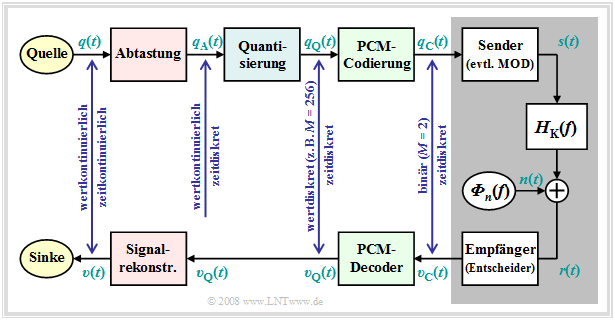
Die Abtastung – also die Zeitdiskretisierung des Analogsignals $q(t)$ – wurde im Kapitel 5.1 des Buches „Signaldarstellung” ausführlich behandelt. Hier folgt eine Kurzzusammenfassung dieses Abschnitts.
Die Grafik verdeutlicht die Abtastung im Zeitbereich. Das (blaue) Signal $q(t)$ ist zeitkontinuierlich und das im Abstand $T_{\rm A}$ abgetastete (grüne) Signal $q_{\rm A}(t)$ zeitdiskret. Dabei gilt:
- Die Abtastung lässt sich durch die Multiplikation des Analogsignals $q(t)$ mit dem Diracpuls $p_δ(t)$ darstellen, der sich auf den Zeitbereich bezieht:
$$q_{\rm A}(t) = q(t) \cdot p_{\delta}(t)\hspace{0.3cm} {\rm mit}\hspace{0.3cm}p_{\delta}(t)= \sum_{\nu = -\infty}^{\infty}T_{\rm A}\cdot \delta(t - \nu \cdot T_{\rm A}) \hspace{0.05cm}.$$
- Das Gewicht der Diracfunktion bei $t = ν · T_{\rm A}$ ist gleich $T_{\rm A} · q(ν · T_{\rm A})$. Da die Diracfunktion $δ(t)$ die Einheit 1/s aufweist, hat somit $q_{\rm A}(t)$ die gleiche Einheit wie $q(t)$, zum Beispiel „V”.
- Die Fouriertransformierte des Diracpulses ist ebenfalls ein Diracpuls (im Frequenzbereich), wobei der Abstand der einzelnen Diraclinien $f_{\rm A} = 1/T_{\rm A}$ beträgt. Alle Impulsgewichte von $P_δ(f)$ sind 1:
$$p_{\delta}(t)= \sum_{\nu = -\infty}^{+\infty}T_{\rm A}\cdot \delta(t - \nu \cdot T_{\rm A}) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f)= \sum_{\mu = -\infty}^{+\infty} \delta(f - \mu \cdot f_{\rm A}) \hspace{0.05cm}.$$
- Das Spektrum $Q_{\rm A}(f)$ des abgetasteten Signals ergibt sich aus dem Faltungssatz, wobei $Q(f)$ das kontinuierliche Spektrum des Analogsignals $q(t)$ bezeichnet:
$$Q_{\rm A}(f) = Q(f) \star P_{\delta}(f)= \sum_{\mu = -\infty}^{+\infty} Q(f - \mu \cdot f_{\rm A}) \hspace{0.05cm}.$$
Diese Gleichungen werden im nächsten Abschnitt durch ein Beispiel verdeutlicht.
Wir weisen Sie hier auf den zweiten Teil des Lernvideos Pulscodemodulation (Dauer 12:53) hin, das die Abtastung und die Signalrekonstruktion systemtheoretisch erklärt.
Abtastung und Signalrekonstruktion (2)
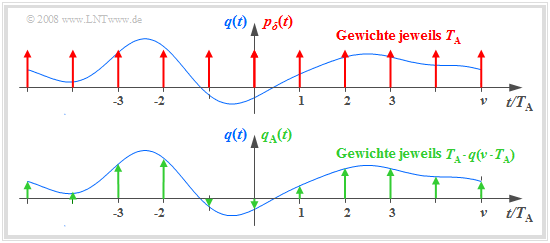
Die obere Grafik zeigt schematisch das Spektrum $Q(f)$ eines analogen Quellensignals $q(t)$, das Frequenzen bis $f_{\rm N, max} =$ 5 kHz beinhaltet. Tastet man das Signal mit der Abtastrate $f_{\rm A} =$ 20 kHz (also im jeweiligen Abstand $T_{\rm A} =$ 50 μs) ab, so erhält man das grün skizzierte periodische Spektrum $Q_{\rm A}(f)$. Da die Diracfunktionen unendlich schmal sind, beinhaltet $q_{\rm A}(t)$ auch beliebig hochfrequente Anteile und dementsprechend ist $Q_{\rm A}(f)$ bis ins Unendliche ausgedehnt (mittlere Grafik). Darunter (rot) gezeichnet ist das Spektrum $Q_{\rm A}(f)$ für die Abtastparameter $T_{\rm A} =$ 100 μs ⇒ $f_{\rm A} =$ 10 kHz.
Aus diesem Beispiel lassen sich folgende wichtige Erkenntnisse bezüglich der Abtastung gewinnen:
- Beinhaltet $Q(f)$ Frequenzen bis $f_{\rm N, max}$, so muss die Abtastrate $f_{\rm A} ≥ 2 · f_{\rm N, max}$ gewählt werden ⇒ Abtasttheorem. Bei kleinerer Abtastrate $f_{\rm A}$ (also größerem Abtastabstand $T_{\rm A}$) kommt es zu Überlappungen der periodifizierten Spektren und damit zu irreversiblen Verzerrungen.
- Gilt exakt $f_{\rm A} = 2 · f_{\rm N, max}$ wie in der unteren Grafik des obigen Beispiels, so kann $Q(f)$ aus $Q_{\rm A}(f)$ – bzw. im PCM–System $V(f)$ aus $V_{\rm Q}(f)$ – durch einen idealen rechteckförmigen Tiefpass $H(f)$ mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2$ vollständig rekonstruiert werden.
- Erfolgt dagegen die Abtastung mit $f_{\rm A} > 2 · f_{\rm N, max}$ wie in der mittleren Grafik des Beispiels, so kann empfängerseitig zur Signalrekonstruktion auch ein Tiefpass $H(f)$ mit kleinerer Flankensteilheit verwendet werden, solange die folgende Bedingung erfüllt ist:
$$H(f) = \left\{ \begin{array}{l} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| \le f_{\rm N, \hspace{0.05cm}max},} \\ {\hspace{0.04cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge f_{\rm A}- f_{\rm N, \hspace{0.05cm}max}.} \\ \end{array}$$
Natürliche und diskrete Abtastung (1)
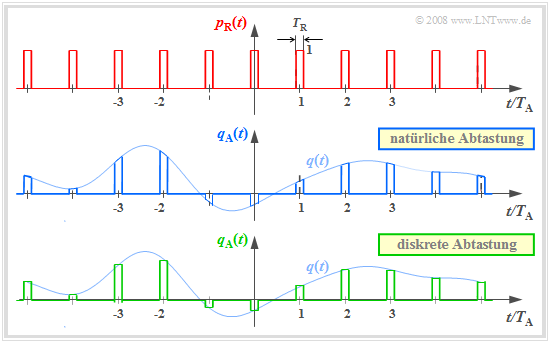
Die Multiplikation mit dem Diracpuls liefert nur eine idealisierte Beschreibung der Abtastung, da eine Diracfunktion (Dauer $T_{\rm R} → 0$, Höhe $1/T_{\rm R} → ∞$) nicht realisierbar ist. In der Praxis muss der Diracpuls $p_δ(t)$ zum Beispiel durch einen Rechteckpuls $$p_{\rm R}(t)= \sum_{\nu = -\infty}^{+\infty}g_{\rm R}(t - \nu \cdot T_{\rm A})\hspace{0.3cm} {\rm mit}\hspace{0.3cm} g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c}{\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \\{\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm} \\ \end{array}$$ ersetzt werden, wobei die Rechteckimpulsdauer $T_{\rm R}$ deutlich kleiner als der Abtastabstand $T_{\rm A}$ sein sollte.
Die Grafik zeigt oben den Rechteckpuls $p_{\rm R}(t)$. Darunter sind zwei verschiedene Abtastverfahren mit diesem Rechteckpuls dargestellt:
- Bei der natürlichen Abtastung ergibt sich das abgetastete Signal $q_{\rm A}(t)$ durch die Multiplikation von $q(t)$ mit $p_{\rm R}(t)$. In den Bereichen $p_{\rm R}(t) =$ 1 hat somit $q_{\rm A}(t)$ den gleichen Verlauf wie $q(t)$.
- Dagegen wird bei der diskreten Abtastung das analoge Signal $q(t)$ – zumindest gedanklich – zuerst mit dem Diracpuls $p_δ(t)$ multipliziert und danach wird jeder Diracimpuls $T_{\rm A} · δ(t – ν · T_{\rm A})$ durch einen Rechteckimpuls $g_{\rm R}(t – ν · T_{\rm A})$ ersetzt.
Hier und bei der im nächsten Abschnitt folgenden Frequenzbereichsbetrachtung ist zur Vereinfachung eine akausale Beschreibungsform gewählt. Für eine (kausale) Realisierung müsste $g_{\rm R}(t) =$ 1 im Bereich von 0 bis $T_{\rm R}$ gelten, und nicht wie hier für $ \ –T_{\rm R}/2 < t < T_{\rm R}/2.$
Natürliche und diskrete Abtastung (2)
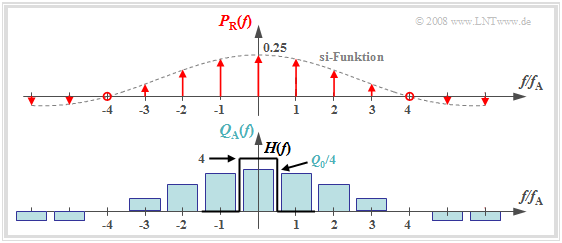
Die natürliche Abtastung lässt sich mit dem Faltungssatz im Spektralbereich wie folgt darstellen: $$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)$$ $$\Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \cdot \frac{1}{T_{\rm A}} \cdot G_{\rm R}(f) \right ] \star Q(f) = P_{\rm R}(f) \star Q(f)\hspace{0.05cm}.$$
Die Grafik zeigt das Ergebnis für
- ein rechteckförmiges Spektrum $Q(f) = Q_0$, das auf den Bereich $|f| ≤$ 4 kHz begrenzt ist,
- die Abtastrate $f_{\rm A} =$ 10 kHz ⇒ $T_{\rm A} =$ 100 μs sowie
- die Rechteckimpulsdauer $T_{\rm R} =$ 25 μs ⇒ $T_{\rm R}/T_{\rm A} =$ 0.25.
Man erkennt aus dieser Darstellung:
- Das Spektrum $P_{\rm R}(f)$ ist im Gegensatz zu $P_δ(f)$ kein Diracpuls (alle Gewichte gleich 1), sondern die Impulsgewichte sind hier mit der Funktion $G_{\rm R}(f)/T_{\rm A} = T_{\rm R}/T_{\rm A} · {\rm si}(πfT_{\rm R})$ bewertet. Auf Grund der Nullstelle der si–Funktion verschwinden die Diraclinien bei $±4f_{\rm A}$ vollständig.
- Das Spektrum $Q_{\rm A}(f)$ ergibt sich aus der Faltung mit $Q(f)$. Das Rechteckspektrum um $f =$ 0 hat die Höhe $T_{\rm R}/T_{\rm A} · Q_0$, die Anteile um $\mu · f_{\rm A} (\mu ≠ 0)$ sind weniger hoch.
- Verwendet man zur Signalrekonstruktion einen idealen, rechteckförmigen Tiefpass
$$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} = 4 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}, \\ \end{array}$$
- so gilt für das Ausgangsspektrum $V(f) = Q(f)$ und dementsprechend ist auch $υ(t) = q(t)$.
Dieses Ergebnis kann wie folgt zusammengefasst werden:
- Bei natürlicher Abtastung kann zur Signalrekonstruktion wie bei der idealen Abtastung (mit einem Diracpuls) ein idealer rechteckförmiger Tiefpass verwendet werden.
- Allerdings muss zur Amplitudenanpassung im Durchlassbereich eine Verstärkung um den Faktor $T_{\rm A}/T_{\rm R}$ berücksichtigt werden.
Natürliche und diskrete Abtastung (3)
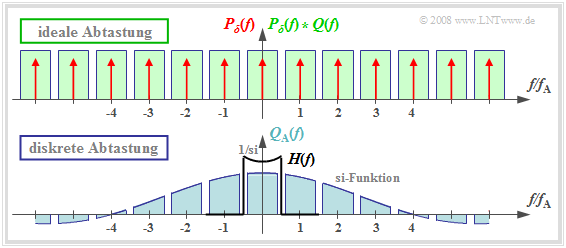
Bei der diskreten Abtastung erfolgt – zumindest gedanklich – zunächst die Multiplikation des Diracpulses $p_δ(t)$ mit dem Quellensignal $q(t)$ und erst danach die Faltung mit dem Rechteckimpuls $g_{\rm R}(t)$: $$q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \cdot q(t)\right ]\star g_{\rm R}(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \star Q(f) \right ] \cdot G_{\rm R}(f)/{T_{\rm A}} \hspace{0.05cm}.$$ Es ist unerheblich, aber durchaus zweckmäßig, dass hier der Faktor $1/T_{\rm A}$ zur Bewertungsfunktion $G_{\rm R}(f)$ hinzugefügt wurde. Damit gilt wieder $G_{\rm R}(f)/T_{\rm A} = T_{\rm R}/T_{\rm A} · {\rm si}(πfT_{\rm R}).$
Die obere Grafik zeigt die Spektralfunktion $P_δ(f) \star Q(f)$ nach idealer Abtastung. Bei diskreter Abtastung mit einem Rechteckpuls ergibt sich dagegen das Spektrum $Q_{\rm A}(f)$ entsprechend dem unteren Diagramm. Man erkennt:
- Jedes der unendlich vielen Teilspektren hat nun eine andere Form. Wichtig ist allerdings nur das Spektrum mit der Mitte bei der Frequenz $f =$ 0, da alle anderen Spektralanteile empfängerseitig durch den Tiefpass der Signalrekonstruktion entfernt werden.
- Verwendet man für diesen Tiefpass wieder ein Rechteckfilter mit der Verstärkung um $T_{\rm A}/T_{\rm R}$ im Durchlassbereich, so erhält man für das Ausgangsspektrum:
$$V(f) = Q(f) \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.05cm}.$$
- Das bedeutet: Bei diskreter Abtastung und Rechteckfilterung kommt es zu Dämpfungsverzerrungen entsprechend der Bewertungsfunktion ${\rm si}(πfT_{\rm R})$. Diese sind um so stärker, je größer $T_{\rm R}$ ist. Nur im Grenzfall $T_{\rm R} → 0$ gilt ${\rm si}(πfT_{\rm R}) =$ 1.
- Allerdings können durch eine ideale Entzerrung diese linearen Dämpfungsverzerrungen vollständig kompensiert werden. Mit
$$H(f) = \left\{ \begin{array}{l} (T_{\rm A}/T_{\rm R})/{\rm si}(\pi f T_{\rm R}) \\ 0 \\ \end{array} \right.\quad\begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2} \\ \end{array}$$
- erhält man $V(f) = Q(f)$ bzw. $υ(t) = q(t)$.