Difference between revisions of "Aufgaben:Exercise 1.2: Decimal/Binary Converter"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Mengentheoretische Grundlagen}} ==A1.2 Schaltlogik (D/B-Wandler)== right| E…“) |
|||
| Line 18: | Line 18: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welche Aussagen sind bezüglich der Zufallsgröße $U$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $U$ beinhaltet 2 Elemente. |
| − | + | + | + $U$ beinhaltet 4 Elemente. |
| − | - | + | - Das kleinste Element von $U$ ist 4. |
| + | + Das größte Element von $U$ ist 14. | ||
| − | {Welche Aussagen sind | + | {Welche Aussagen sind bezüglich der Zufallsgröße $V$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $V$ beinhaltet 2 Elemente. |
| − | - | + | - $V$ beinhaltet 4 Elemente. |
| − | - | + | + Das kleinste Element von $V$ ist 4. |
| + | - Das größte Element von $V$ ist 14. | ||
| − | {Welche Aussagen sind | + | {Welche Aussagen sind bezüglich der Zufallsgröße $W$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $W$ beinhaltet 2 Elemente. |
| − | - Das | + | - $W$ beinhaltet 4 Elemente. |
| − | + | - Das kleinste Element von $W$ ist 4. | |
| + | - Das größte Element von $W$ ist 14. | ||
| − | { | + | {Welche Aussagen sind bezüglich der Zufallsgröße $P$ zutreffend? |
| − | |type=" | + | |type="[]"} |
| − | + | - $P$ beinhlatet alle Zweierpotenzen. | |
| − | + | + $P$ beinhaltet alle Primzahlen. | |
| − | <math> \ | + | - $P$ beschreibt die leere Menge <math>\phi</math> . |
| + | - $P$ ist identisch mit der Grundmenge $G = {1,2, ... , 15}$. | ||
</quiz> | </quiz> | ||
Revision as of 19:39, 28 August 2016
A1.2 Schaltlogik (D/B-Wandler)
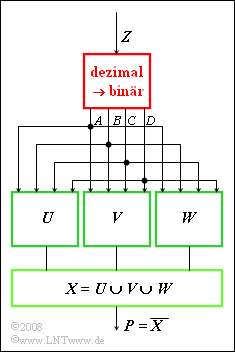
Ein Zahlengenerator $Z$ liefert Dezimalwerte im Bereich von 1 bis 15. Diese werden in Binärzahlen umgewandelt (rot umrandeter Block). Der Ausgang besteht aus den vier Binärwerten $A$, $B$, $C$ und $D$ mit abnehmender Wertigkeit. Beispielsweise liefert $Z = 11$ die Binärwerte $$ A = 1, B = 0, C = 1, D = 1. $$ Mengentheoretisch lässt sich dies wie folgt darstellen: $$ Z = 11\qquad\widehat{=}\qquad A \cap\bar{ B} \cap C \cap D$$ Aus den binären Größen A, B, C und D werden drei weitere Boolsche Ausdrücke gebildet, deren Vereinigungsmenge mit X bezeichnet wird: \[ U = A \cap \bar{D} \] \[ V = \bar{A} \cap B \cap \bar{D} \] $$W, wobei \, \bar{W} = \bar{A} \cup \bar{D} \cup (\bar{B} \cap C) \cup (B \cap \bar{C}). $$ Für die folgenden Fragen ist zu berücksichtigen, dass $Z = 0 ⇒ A = B = C = D = 0$ bereits durch den Zahlengenerator ausgeschlossen ist. Beachten Sie ferner, dass nicht alle Eingangsgrößen $A$, $B$, $C$ und $D$ zur Berechnung aller Zwischengrößen $U$, $V$ und $W$ herangezogen werden. Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.2. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:
Fragebogen zu "A1.2 Schaltlogik (D/B-Wandler)"
Musterlösung