Difference between revisions of "Aufgaben:Exercise 2.1: Election Demand"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Wahrscheinlichkeit und relative Häufigkeit }} right| :Zu einer Bür…“) |
|||
| Line 57: | Line 57: | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| + | Category:Aufgaben zu Stochastische Signaltheorie|^2.1 Wahrscheinlichkeit und relative Häufigkeit^ | ||
| − | + | [[Category:Aufgaben zu Stochastische Signaltheorie|^2.1 Vom Zufallsexperiment zur Zufallsgröße^]] | |
| − | [[Category:Aufgaben zu Stochastische Signaltheorie|^2.1 | ||
Revision as of 17:21, 1 March 2017
- Zu einer Bürgermeisterwahl treten die drei Kandidaten A, B und C an. Gewählt ist derjenige Kandidat, der mehr als 50% der abgegebenen Stimmen erhält. Gelingt dies im ersten Wahlgang keinem der drei Bewerber, so kommt es zwischen den beiden Kandidaten mit den meisten Stimmen zu einer Stichwahl.
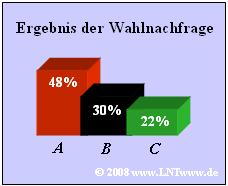
- Direkt nach Schließung der Wahllokale wird das Ergebnis einer Wahlnachfrage vorgelegt:
- Kandidat A: 48%, Kandidat B: 30%, Kandidat C: 22%.
- Diese Nachfrage basiert auf einer Umfrage unter lediglich N = 2000 der insgesamt N ' = 800.000 Wählerinnen und Wähler. Gehen Sie bei der Beantwortung der nachfolgenden Fragen von folgenden Voraussetzungen aus:
- Die bei der Wahl von den Kandidaten A, B und C tatsächlich erzielten Stimmen können als die Wahrscheinlichkeiten pA, pB und pC aufgefasst werden, obwohl auch diese selbst als relative Häufigkeiten (bezogen auf N ') ermittelt werden.
- Die 2000 ausgewählten Wähler repräsentieren die gesamte Wählerschaft im statistischen Sinne ideal und haben bei der Wahlnachfrage wahrheitsgemäß geantwortet.
- Nach dem Bernoullischen Gesetz der großen Zahlen sollen die Ergebnisse dieser Nachfrage als relative Häufigkeiten aufgefasst werden: hA = 0.48, hB = 0.3, hC = 0.22.
- Hinweis: Die Aufgabe bezieht sich auf das Kapitel 2.1. Diese Thematik ist in dem folgenden Lernvideo zusammengefasst:
Fragebogen
Musterlösung
- 1. Man sollte dieser Nachfrage zumindest glauben, dass Kandidat A wahrscheinlich gewinnt.
- 2. Die Wahrscheinlichkeit, dass die Nachfrage (hA) vom endgültigen Ergebnis (pA) betragsmäßig um mehr als 2% abweicht, ist nach dem Bernouillischen Gesetz der großen Zahlen mit N = 2000:
- $$Pr(|h_A - p_A| \geq 0.02) \leq \frac{1}{4 \cdot 2000\cdot 0.02^2} = 0.3125.$$
- Diese Wahrscheinlichkeit beinhaltet die beiden Fälle, dass pA ≤ 46% und pA ≥ 50% ist. Nur im letzten Fall gibt es keine Stichwahl:
- $$\rm Pr(keine\hspace{0.1cm}Stichwahl)\le 15.6 \%\hspace{0.15cm}\underline{= 0.156}.$$
- 3. Mit ε = 4% (ergibt sich aus 0.26 – 0.22) liefert das Gesetz der großen Zahlen:
- $$\rm Pr\left(|\it h_{\rm C}-p_{\rm C}|\ge \rm 0.04\right)\le\rm\frac{1}{4\cdot 2000\cdot 0.04^2}=0.078.$$
- Daraus folgt: Die Wahrscheinlichkeit, dass Kandidat C mindestens 26% der Stimmen erhält, ist nicht größer als 3.9%.
- Da pA = 0.48 fest vorausgesetzt wurde, gilt in diesem Fall gleichzeitig pB ≤ 0.26. Da es sich hier um kontinuierliche Zufallsgrößen handelt, sind (pC ≥ 0.26; pB ≤ 0.26) und (pC > 0.26; pB < 0.26) gleich. Damit ist die Wahrscheinlichkeit, dass C die Stichwahl) erreicht, ebenfalls auf 3.9% beschränkt:
- $$\rm Pr(C\hspace{0.1cm}erreicht\hspace{0.1cm}Stichwahl)\le 3.9 \%\hspace{0.15cm}\underline{= 0.039}.$$
Category:Aufgaben zu Stochastische Signaltheorie|^2.1 Wahrscheinlichkeit und relative Häufigkeit^