Aufgaben:Exercise 4.16: Eigenvalues and Eigenvectors

• Return to book

Obwohl die Beschreibung Gaußscher Zufallsgrößen mit Hilfe von Vektoren und Matrizen eigentlich nur bei mehr als N = 2 Dimensionen erforderlich ist und Sinn macht, beschränken wir uns hier auf den Sonderfall zweidimensionaler Zufallsgrößen.

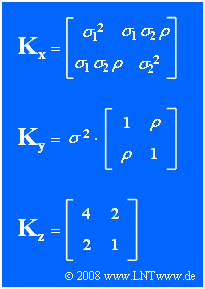
In der Grafik ist oben die allgemeine Korrelationsmatrix K_x der 2D–Zufallsgröße x = (x₁, x₂)^T angegeben, wobei σ₁² und σ₂² die Varianzen der Einzelkomponenten beschreiben. ρ bezeichnet den Korrelationskoeffizienten zwischen den beiden Komponenten.

Die Zufallsgrößen y und z geben zwei Spezialfälle von x an, deren Prozessparameter aus den Kovarianzmatrizen K_y und K_z bestimmt werden können.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.7. Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den folgenden Seiten:
     Determinante einer Matrix,
     Inverse einer Matrix.

Weiterhin ist zu beachten:

• Eine 2×2-Kovarianzmatrix besitzt zwei reelle Eigenwerte λ₁ und λ₂.
  

• Die beiden Eigenwerte bestimmen zwei Eigenvektoren ξ₁ und ξ₂ und diese spannen ein neues Koordinatensystem in Richtung der Hauptachsen des alten Systems auf.

• Entsprechend der Seite Höhenlinien bei korrelierten Zufallsgrößen ist der Winkel α zwischen dem alten und dem neuen System durch folgende Gleichung gegeben:

$$\alpha = \frac{1}{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$

Fragebogen

1

Multiple-Choice Frage

	Falsch
	Richtig

2

Input-Box Frage

$\alpha$ =

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.