Difference between revisions of "Aufgaben:Exercise 4.1: Attenuation Function"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1797__LZI_A_4_1.png|right|]] | + | [[File:P_ID1797__LZI_A_4_1.png|right|Dämpfungsmaß und Schranken]] |
| − | + | Das Dämpfungsmaß $\alpha(f)$ – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an. Diese Größe ist durch die Leitungsbeläge $R'$, $L'$, $G'$ und $C'$ festgelegt, wobei die exakte Gleichung etwas kompliziert ist. Daher wurden zwei leichter handhabbare Näherungen entwickelt: | |
| − | + | $$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R' \cdot \sqrt{{C'}/{ L'} } + G' \cdot \sqrt{{L'}/{ C'} }\right ] | |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | + | $$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R' \cdot C'} }\hspace{0.1cm} | |
\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ | \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ | ||
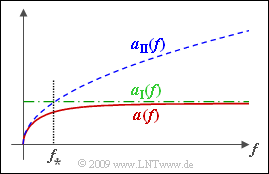
| − | + | Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf $\alpha(f)$ in der Grafik dargestellt. Der Schnittpunkt von $\alpha_{\rm I}(f)$ und $\alpha_{\rm II}(f)$ ergibt die charakteristische Frequenz $f_∗$ mit folgender Bedeutung: | |
| + | *Für $f \gg f_∗$ gilt $α(f) ≈ α_{\rm I}(f)$. | ||
| + | *Für $f \ll f_∗$ gilt $α(f) ≈ α_{\rm II}(f)$. | ||
| − | + | Mit diesen Näherungen soll das Dämpfungsmaß $\alpha(f)$ für ein Nachrichtensignal der Frequenz $f_0 = 2 \ \rm kHz ermittelt werden, wobei folgende Übertragungsmedien zu betrachten sind: | |
| − | + | * ein Kupferkabel mit 0.6 mm Durchmesser: | |
| − | |||
| − | |||
| − | |||
| − | |||
:$$R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | :$$R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | ||
L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
| Line 23: | Line 21: | ||
C\hspace{0.03cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$ | C\hspace{0.03cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$ | ||
| − | + | * eine Bronzefreileitung mit 5 mm Durchmesser: | |
:$$R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | :$$R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | ||
L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
Revision as of 14:24, 14 February 2017
Das Dämpfungsmaß $\alpha(f)$ – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an. Diese Größe ist durch die Leitungsbeläge $R'$, $L'$, $G'$ und $C'$ festgelegt, wobei die exakte Gleichung etwas kompliziert ist. Daher wurden zwei leichter handhabbare Näherungen entwickelt: $$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R' \cdot \sqrt{{C'}/{ L'} } + G' \cdot \sqrt{{L'}/{ C'} }\right ] \hspace{0.05cm},$$ $$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R' \cdot C'} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf $\alpha(f)$ in der Grafik dargestellt. Der Schnittpunkt von $\alpha_{\rm I}(f)$ und $\alpha_{\rm II}(f)$ ergibt die charakteristische Frequenz $f_∗$ mit folgender Bedeutung:
- Für $f \gg f_∗$ gilt $α(f) ≈ α_{\rm I}(f)$.
- Für $f \ll f_∗$ gilt $α(f) ≈ α_{\rm II}(f)$.
Mit diesen Näherungen soll das Dämpfungsmaß $\alpha(f)$ für ein Nachrichtensignal der Frequenz $f_0 = 2 \ \rm kHz ermittelt werden, wobei folgende Übertragungsmedien zu betrachten sind:
- ein Kupferkabel mit 0.6 mm Durchmesser:
- $$R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 1\,\,{\rm \mu S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$
- eine Bronzefreileitung mit 5 mm Durchmesser:
- $$R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 0.5\,\,{\rm \mu S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
- Die Aufgabe gehört zum Themenkomplex von Kapitel 4.1.
Fragebogen
Musterlösung
- 1. Für das Kupferkabel gilt mit R' = 130 Ω/km, L' = 0.6 mH/km, G' = 1 μs/km und C' = 35 nF/km:
- $${\alpha_{_{\rm I}}(f)} = \frac{1 \,\rm Np/km}{2} \cdot \left [130\,{\rm \Omega} \cdot \sqrt{\frac{35 \cdot 10^{-9}\,{\rm s/\Omega}}{ 0.6 \cdot 10^{-3}\,{\rm \Omega \,s}} } + 10^{-6}\,{\rm \Omega^{-1}} \cdot \sqrt{\frac{0.6 \cdot 10^{-3}\,{\rm \Omega \,s}}{ 35 \cdot 10^{-9}\,{\rm s/\Omega}} }\hspace{0.1cm}\right ]= \\ = \frac{1 \,\rm Np/km}{2} \cdot \left [130 \cdot 7.638 \cdot 10^{-3}+ 10^{-6} \cdot 0.131 \cdot 10^{3}\right ]= \\ = \frac{1 \,\rm Np/km}{2} \cdot$$
- Für die Bronzeleitung ergibt sich mit R' = 2.2 Ω/km, L' = 1.8 mH/km, G' = 0.5 μs/km, C' = 6.7 nF/km:
- $${\alpha_{_{\rm I}}(f)} = \frac{1 \,\rm Np/km}{2} \cdot \left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } + 0.5 \cdot 10^{-6} \cdot \sqrt{\frac{ 1.8 \cdot 10^{-3}} {6.7 \cdot 10^{-9}}}\hspace{0.1cm}\right ]= \\ = \frac{1 \,\rm Np/km}{2} \cdot \left [4.244 \cdot 10^{-3}+ 0.259 \cdot 10^{-3}\right ] \hspace{0.15cm}\underline{= 2.25\cdot 10^{-3}\,{\rm Np}/{ {\rm km} }}\hspace{0.05cm}.$$
- 2. Die unter a) berechnete Schranke αI(f) gilt nur für f >> f∗, während die Schranke αII(f) für f << f∗ gültig ist. Die charakteristische Frequenz ergibt sich als der Schnittpunkt der beiden Näherungen:
- $${\alpha_{_{\rm II}}(f = f_{\star})} = \sqrt{\omega_{\star} \cdot \frac{R' \hspace{0.05cm} C'}{ 2} }\hspace{0.1cm} \bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = {\alpha_{_{\rm I}}(f = f_{\star})}$$
- Für das Kupferkabel mit 0.6 mm Durchmesser gilt folgende Bestimmungsgleichung:
- $$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= \frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} \hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$
- Dagegen erhält man für die Bronzeleitung mit 5 mm Durchmesser:
- $$f_{\star} = \frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} \hspace{0.15cm}\underline{= 0.109\,{\rm kHz}}\hspace{0.05cm}.$$
- 3. Für das Kupferkabel gilt f0 << f∗. Deshalb ist hier die Näherung αII(f) günstiger:
- $$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} \hspace{0.1cm}\frac{\rm Np}{ {\rm km} } \hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$
- Dagegen ist für die Bronzeleitung wegen f0 >> f∗ die Näherung αI(f) – die so genannte „schwache Dämpfung” – besser geeignet (siehe Teilaufgabe 1)):
- $$\alpha(f = f_0) \hspace{0.15cm}\underline{= 2.25 \cdot 10^{-3}\hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$