Difference between revisions of "Digital Signal Transmission/Properties of Nyquist Systems"
| Line 32: | Line 32: | ||
<br> | <br> | ||
Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.<br> | Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.<br> | ||
| − | Erstes Nyquistkriterium: Erfüllt das Spektrum <i>G<sub>d</sub></i>(<i>f</i>) des Detektionsgrundimpulses die Bedingung<br> | + | Erstes Nyquistkriterium: Erfüllt das Spektrum <i>G<sub>d</sub></i>(<i>f</i>) des Detektionsgrundimpulses die Bedingung<br><br> |
| − | <math>\ | + | <math>\sum \limits {\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= |
| − | g_0 \cdot T = {\rm const.} \hspace{0.05cm}, </math><br> | + | g_0 \cdot T = {\rm const.} \hspace{0.05cm}, </math><br><br> |
so ist <i>g<sub>d</sub></i>(<i>t</i>) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten | so ist <i>g<sub>d</sub></i>(<i>t</i>) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten | ||
<i>νT</i> (<i>ν</i> ≠ 0) und der Amplitude <i>g<sub>d</sub></i>(<i>t</i> = 0) = <i>g</i><sub>0</sub>. <i>Hinweis</i>: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.<br> | <i>νT</i> (<i>ν</i> ≠ 0) und der Amplitude <i>g<sub>d</sub></i>(<i>t</i> = 0) = <i>g</i><sub>0</sub>. <i>Hinweis</i>: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.<br> | ||
| − | Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum<br> | + | Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum<br><br> |
<math>G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\ | <math>G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| Line 44: | Line 44: | ||
|f| < {1}/({2T})\hspace{0.05cm}, \\ | |f| < {1}/({2T})\hspace{0.05cm}, \\ | ||
|f| > {1}/({2T}) \hspace{0.1cm} \\ | |f| > {1}/({2T}) \hspace{0.1cm} \\ | ||
| − | \end{array}</math><br> | + | \end{array}</math><br><br> |
| − | erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls <i>g</i><sub>1</sub>(<i>t</i>) = <i>g</i><sub>0</sub> · si(π<i>t</i>/<i>T</i>) klingt sehr langsam ab, nämlich asymptotisch mit 1/<i>t</i>.<br> | + | erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls <i>g</i><sub>1</sub>(<i>t</i>) = <i>g</i><sub>0</sub> · si(π<i>t</i>/<i>T</i>) klingt sehr langsam ab, nämlich asymptotisch mit 1/<i>t</i>.<br><br> |
| − | [[File:P_ID1273__Dig_T_1_3_S2_v1.png|Zur Verdeutlichung des ersten Nyquistkriteriums|class=fit]]<br> | + | [[File:P_ID1273__Dig_T_1_3_S2_v1.png|Zur Verdeutlichung des ersten Nyquistkriteriums|class=fit]]<br><br> |
| − | Der rechts oben dargestellte Realteil des Spektrums <i>G</i><sub>2</sub>(<i>f</i>) wurde aus dem Rechteckspektrum <i>G</i><sub>1</sub>(<i>f</i>) durch Verschiebung von Teilstücken um 1/<i>T</i> nach rechts oder links konstruiert. Wegen <br> | + | Der rechts oben dargestellte Realteil des Spektrums <i>G</i><sub>2</sub>(<i>f</i>) wurde aus dem Rechteckspektrum <i>G</i><sub>1</sub>(<i>f</i>) durch Verschiebung von Teilstücken um 1/<i>T</i> nach rechts oder links konstruiert. Wegen <br><br> |
<math>\sum_{k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f - | <math>\sum_{k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f - | ||
\frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm}, | \frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm}, | ||
\hspace{1cm}\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f - | \hspace{1cm}\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f - | ||
| − | \frac{k}{T} \right)\right]= 0</math><br> | + | \frac{k}{T} \right)\right]= 0</math><br><br> |
handelt es sich bei <i>G</i><sub>2</sub>(<i>f</i>) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/<i>T</i> auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses <i>g</i><sub>2</sub>(<i>t</i>) ist allerdings sehr kompliziert. | handelt es sich bei <i>G</i><sub>2</sub>(<i>f</i>) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/<i>T</i> auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses <i>g</i><sub>2</sub>(<i>t</i>) ist allerdings sehr kompliziert. | ||
{{Display}} | {{Display}} | ||
Revision as of 14:48, 21 November 2016
Erstes Nyquistkriterium im Zeitbereich
Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals
\(d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)\)
zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls gd(t)
- auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
- äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.
Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal dN(t) als vernachlässigbar klein angenommen.
- \[g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\]
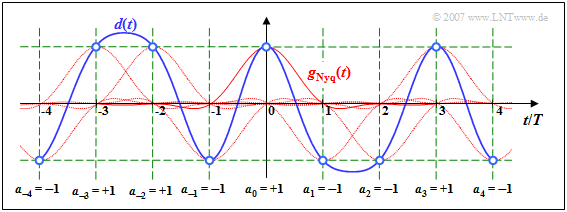
Zu den Detektionszeitpunkten gilt d(νT) = aν · gNyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a0 nicht.
Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls
\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot
t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot
T}\right)\)
Erstes Nyquistkriterium im Frequenzbereich
Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.
Erstes Nyquistkriterium: Erfüllt das Spektrum Gd(f) des Detektionsgrundimpulses die Bedingung
\(\sum \limits {\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)=
g_0 \cdot T = {\rm const.} \hspace{0.05cm}, \)
so ist gd(t) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten
νT (ν ≠ 0) und der Amplitude gd(t = 0) = g0. Hinweis: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.
Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum
\(G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\
0 \\ \end{array} \right.\quad
\begin{array}{*{1}c} {\rm{f\ddot{u}r}}
\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}
|f| < {1}/({2T})\hspace{0.05cm}, \\
|f| > {1}/({2T}) \hspace{0.1cm} \\
\end{array}\)
erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls g1(t) = g0 · si(πt/T) klingt sehr langsam ab, nämlich asymptotisch mit 1/t.
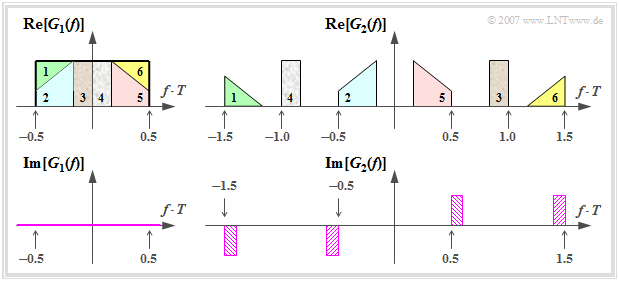
Der rechts oben dargestellte Realteil des Spektrums G2(f) wurde aus dem Rechteckspektrum G1(f) durch Verschiebung von Teilstücken um 1/T nach rechts oder links konstruiert. Wegen
\(\sum_{k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f -
\frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm},
\hspace{1cm}\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f -
\frac{k}{T} \right)\right]= 0\)
handelt es sich bei G2(f) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/T auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses g2(t) ist allerdings sehr kompliziert.