Difference between revisions of "Information Theory/Natural Discrete Sources"
m (Markus verschob die Seite Informationstheorie und Quellencodierung/Natürliche wertdiskrete Nachrichtenquellen nach Informationstheorie/Natürliche wertdiskrete Nachrichtenquellen, ohne dabei eine Weiterleitung anzulegen) |
|||
| Line 16: | Line 16: | ||
| − | Theoretisch könnte man auch hier die Entropie entsprechend der Vorgehensweise in Kapitel 1.2 als den Grenzübergang der Entropienäherung $H_k$ für $k$ → ∞ ermitteln. Praktisch ergeben sich aber nach dieser Rezeptur unüberwindbare numerische Grenzen: | + | Theoretisch könnte man auch hier die Entropie entsprechend der Vorgehensweise in [[Verallgemeinerung auf k–Tupel und Grenzübergang|Kapitel 1.2]] als den Grenzübergang der Entropienäherung $H_k$ für $k$ → ∞ ermitteln. Praktisch ergeben sich aber nach dieser Rezeptur unüberwindbare numerische Grenzen: |
*Bereits für die Entropienäherung $H_2$ gibt es $M_2$ = $256^2$ = 65536 mögliche Zweiertupel. Für die Berechnung sind somit ebenso viele Speicherplätze (in Byte) erforderlich. Geht man davon aus, dass man für eine ausreichend sichere Statistik im Mittel 100 Entsprechungen pro Tupel benötigt, so sollte die Länge der Quellensymbolfolge bereits N > $6.5 · 10^6$ sein. | *Bereits für die Entropienäherung $H_2$ gibt es $M_2$ = $256^2$ = 65536 mögliche Zweiertupel. Für die Berechnung sind somit ebenso viele Speicherplätze (in Byte) erforderlich. Geht man davon aus, dass man für eine ausreichend sichere Statistik im Mittel 100 Entsprechungen pro Tupel benötigt, so sollte die Länge der Quellensymbolfolge bereits N > $6.5 · 10^6$ sein. | ||
*Die Anzahl der möglichen Dreiertupel ergibt sich zu $M_3$ > $16 · 10^7$ und damit ist die erforderliche Quellensymbollänge $N$ schon größer als $1.6 · 10^9$. Dies entspricht bei 42 Zeilen pro Seite und 80 Zeichen pro Zeile einem Buch mit etwa 500.000 Seiten. | *Die Anzahl der möglichen Dreiertupel ergibt sich zu $M_3$ > $16 · 10^7$ und damit ist die erforderliche Quellensymbollänge $N$ schon größer als $1.6 · 10^9$. Dies entspricht bei 42 Zeilen pro Seite und 80 Zeichen pro Zeile einem Buch mit etwa 500.000 Seiten. | ||
*Bei einem natürlichen Text reichen die statistischen Bindungen aber sehr viel weiter als zwei oder drei Zeichen. Küpfmüller gibt für die deutsche Sprache einen Wert von 100 an [Küp54]. Zur Ermittlung der 100. Entropienäherung benötigt man aber $2^{800}$ ≈ $10^{240}$ Häufigkeiten und für die gesicherte Statistik nochmals um den Faktor 100 mehr Zeichen. | *Bei einem natürlichen Text reichen die statistischen Bindungen aber sehr viel weiter als zwei oder drei Zeichen. Küpfmüller gibt für die deutsche Sprache einen Wert von 100 an [Küp54]. Zur Ermittlung der 100. Entropienäherung benötigt man aber $2^{800}$ ≈ $10^{240}$ Häufigkeiten und für die gesicherte Statistik nochmals um den Faktor 100 mehr Zeichen. | ||
| − | Eine berechtigte Frage ist deshalb: Wie hat Karl Küpfmüller im Jahre 1954 die Entropie der deutschen Sprache ermittelt, und vor ihm schon Claude E. Shannon die Entropie der englischen Sprache? Eines sei vorweg verraten: Nicht mit dem oben beschriebenen Ansatz. | + | Eine berechtigte Frage ist deshalb: Wie hat [https://de.wikipedia.org/wiki/Karl_K%C3%BCpfm%C3%BCller Karl Küpfmüller] im Jahre 1954 die Entropie der deutschen Sprache ermittelt, und vor ihm schon [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] die Entropie der englischen Sprache? Eines sei vorweg verraten: Nicht mit dem oben beschriebenen Ansatz. |
| Line 67: | Line 67: | ||
$$H_{5.5} \approx \frac{11}{5.5}\approx 2\,\, {\rm bit/Buchstabe}\hspace{0.05 cm}.$$ | $$H_{5.5} \approx \frac{11}{5.5}\approx 2\,\, {\rm bit/Buchstabe}\hspace{0.05 cm}.$$ | ||
| − | Natürlich kann $k$ gemäß Definition nur ganzzahlige Werte annehmen. Diese Gleichung ist deshalb so zu interpretieren, dass sich für $H_5$ ein etwas größerer und für $H_6$ ein etwas kleinerer Wert ergeben wird. | + | Natürlich kann $k$ gemäß [[Informationstheorie/Nachrichtenquellen_mit_Gedächtnis#Verallgemeinerung_auf_k.E2.80.93Tupel_und_Grenz.C3.BCbergang|Definition]] nur ganzzahlige Werte annehmen. Diese Gleichung ist deshalb so zu interpretieren, dass sich für $H_5$ ein etwas größerer und für $H_6$ ein etwas kleinerer Wert ergeben wird. |
| Line 77: | Line 77: | ||
| − | 7.) Küpfmüller versuchte anschließend, den von ihm gefundenen Endwert $H$ = 1.6 bit/Buchstabe mit völlig anderer Methodik – siehe | + | 7.) Küpfmüller versuchte anschließend, den von ihm gefundenen Endwert $H$ = 1.6 bit/Buchstabe mit völlig anderer Methodik – siehe nächster Abschnitt – zu verifizieren. Nach dieser Abschätzung revidierte er sein Ergebnis geringfügig auf $H$ = 1.51 bit/Buchstabe. |
| Line 119: | Line 119: | ||
''Hinweis'': Betrachten Sie diese Ergebnisse bitte nicht als Teil einer wissenschaftlichen Untersuchung, sondern nur als den Versuch, Studierenden die in Kapitel 1.3 behandelte Thematik in einem Praktikum näher zu bringen. Als Grundlage dieser Untersuchung wurde von der Bibel ausgegangen, da uns sowohl deren deutsche als auch die englische Fassung im geeigneten ASCII–Format zur Verfügung gestellt wurden. | ''Hinweis'': Betrachten Sie diese Ergebnisse bitte nicht als Teil einer wissenschaftlichen Untersuchung, sondern nur als den Versuch, Studierenden die in Kapitel 1.3 behandelte Thematik in einem Praktikum näher zu bringen. Als Grundlage dieser Untersuchung wurde von der Bibel ausgegangen, da uns sowohl deren deutsche als auch die englische Fassung im geeigneten ASCII–Format zur Verfügung gestellt wurden. | ||
| − | Die in der Tabelle angegebenen Entropien $H_0$ (Entscheidungsgehalt), $H_1$, $H_2$ und $H_3$ wurden jeweils aus $N$ Schriftzeichen ermittelt und sind jeweils in bit/Schriftzeichen angegeben. Die gesamte Datei „Bibel” (in deutscher Sprache) beinhaltet fast $N$ = 4.37 Millionen Schriftzeichen, was bei 42 Zeilen pro Seite und 80 Zeichen pro Zeile etwa einem Buch mit 1300 Seiten entsprechen würde. Der Symbolumfang ist $M$ = 33. | + | Die in der [[Natürliche_wertdiskrete_Nachrichtenquellen#Einige_eigene_Simulationsergebnisse|Tabelle]] angegebenen Entropien $H_0$ (Entscheidungsgehalt), $H_1$, $H_2$ und $H_3$ wurden jeweils aus $N$ Schriftzeichen ermittelt und sind jeweils in bit/Schriftzeichen angegeben. Die gesamte Datei „Bibel” (in deutscher Sprache) beinhaltet fast $N$ = 4.37 Millionen Schriftzeichen, was bei 42 Zeilen pro Seite und 80 Zeichen pro Zeile etwa einem Buch mit 1300 Seiten entsprechen würde. Der Symbolumfang ist $M$ = 33. |
Die Ergebnisse lassen sich wie folgt zusammenfassen: | Die Ergebnisse lassen sich wie folgt zusammenfassen: | ||
*In allen Zeilen nehmen die Entropienäherungen $H_k$ mit wachsendem $k$ monoton ab. Der Abfall verläuft konvex, das heißt, es ist $H_1$ – $H_2$ > $H_2$ – $H_3$. Die Extrapolation des Endwertes ( $k$ → ∞ ) ist aus den jeweils ermittelten drei Entropienäherungen nicht (oder nur sehr vage) möglich. | *In allen Zeilen nehmen die Entropienäherungen $H_k$ mit wachsendem $k$ monoton ab. Der Abfall verläuft konvex, das heißt, es ist $H_1$ – $H_2$ > $H_2$ – $H_3$. Die Extrapolation des Endwertes ( $k$ → ∞ ) ist aus den jeweils ermittelten drei Entropienäherungen nicht (oder nur sehr vage) möglich. | ||
| Line 142: | Line 142: | ||
[[File:P_ID2269__Inf_T_1_3_S4.png|Künstlich erzeugte deutsche und englische Texte]] | [[File:P_ID2269__Inf_T_1_3_S4.png|Künstlich erzeugte deutsche und englische Texte]] | ||
| − | Weitere Information zur synthetischen Erzeugung von deutschen und englischen Texten finden Sie in Aufgabe A1.8. | + | Weitere Information zur synthetischen Erzeugung von deutschen und englischen Texten finden Sie in [[Aufgaben:1.8_Synthetisch_erzeugte_Texte|Aufgabe A1.8]]. |
Revision as of 23:18, 29 January 2017
Contents
Schwierigkeiten bei der Entropiebestimmung
Bisher haben wir uns ausschließlich mit künstlich erzeugten Symbolfolgen beschäftigt. Nun betrachten wir geschriebene Texte. Ein solcher Text kann als eine natürliche wertdiskrete Nachrichtenquelle aufgefasst werden, die natürlich auch informationstheoretisch analysiert werden kann, indem man ihre Entropie ermittelt. Natürliche Texte werden auch in heutiger Zeit (2011) noch oft mit dem 8 Bit–Zeichensatz nach ANSI (American National Standard Institute) dargestellt, obwohl es etliche „modernere” Codierungen gibt. Die $M$ = $2^8$ = 256 ANSI–Zeichen sind dabei wie folgt belegt:
- Nr. 0 bis 31: nicht druck– und darstellbare Steuerbefehle,
- Nr. 32 bis 127: identisch mit den Zeichen des 7 Bit–ASCII–Codes,
- Nr. 128 bis 159: weitere Steuerzeichen bzw. Alphanumerikzeichen für Windows,
- Nr. 160 bis 255: identisch mit Unicode–Charts.
Theoretisch könnte man auch hier die Entropie entsprechend der Vorgehensweise in Kapitel 1.2 als den Grenzübergang der Entropienäherung $H_k$ für $k$ → ∞ ermitteln. Praktisch ergeben sich aber nach dieser Rezeptur unüberwindbare numerische Grenzen:
- Bereits für die Entropienäherung $H_2$ gibt es $M_2$ = $256^2$ = 65536 mögliche Zweiertupel. Für die Berechnung sind somit ebenso viele Speicherplätze (in Byte) erforderlich. Geht man davon aus, dass man für eine ausreichend sichere Statistik im Mittel 100 Entsprechungen pro Tupel benötigt, so sollte die Länge der Quellensymbolfolge bereits N > $6.5 · 10^6$ sein.
- Die Anzahl der möglichen Dreiertupel ergibt sich zu $M_3$ > $16 · 10^7$ und damit ist die erforderliche Quellensymbollänge $N$ schon größer als $1.6 · 10^9$. Dies entspricht bei 42 Zeilen pro Seite und 80 Zeichen pro Zeile einem Buch mit etwa 500.000 Seiten.
- Bei einem natürlichen Text reichen die statistischen Bindungen aber sehr viel weiter als zwei oder drei Zeichen. Küpfmüller gibt für die deutsche Sprache einen Wert von 100 an [Küp54]. Zur Ermittlung der 100. Entropienäherung benötigt man aber $2^{800}$ ≈ $10^{240}$ Häufigkeiten und für die gesicherte Statistik nochmals um den Faktor 100 mehr Zeichen.
Eine berechtigte Frage ist deshalb: Wie hat Karl Küpfmüller im Jahre 1954 die Entropie der deutschen Sprache ermittelt, und vor ihm schon Claude E. Shannon die Entropie der englischen Sprache? Eines sei vorweg verraten: Nicht mit dem oben beschriebenen Ansatz.
Entropieabschätzung nach Küpfmüller
Karl Küpfmüller hat die Entropie von deutschen Texten untersucht. Er geht bei seiner in [Küp54] veröffentlichten Abschätzung von folgenden Voraussetzungen aus:
- ein Alphabet mit 26 Buchstaben (keine Umlaute und Satzzeichen),
- Nichtberücksichtigung des Leerzeichens,
- keine Unterscheidung zwischen Groß– und Kleinschreibung.
Der Entscheidungsgehalt ergibt sich somit zu $H_0$ = $\log_2$ (26) ≈ 4.7 bit/Buchstabe.
Seine Abschätzung basiert auf den folgenden Überlegungen:
1.) Die erste Entropienäherung ergibt sich aus den Buchstabenhäufigkeiten in deutschen Texten. Nach einer Studie von 1939 ist „e” mit 16.7% am häufigsten, am seltensten ist „x” mit 0.02%.
$$H_1 \approx 4.1\,\, {\rm bit/Buchstabe}\hspace{0.05 cm}.$$
2.) Hinsichtlich der Silbenhäufigkeit wertet Küpfmüller das von F.W. Kaeding herausgegebene „Häufigkeitswörterbuch der deutschen Sprache” aus. Er unterscheidet zwischen Stammsilben, Vorsilben und Endsilben. Er kommt so auf den mittleren Informationsgehalt aller Silben:
$$}H_{\rm Silbe} = \hspace{-0.1cm} H_{\rm Stamm} + H_{\rm Vor} + H_{\rm End} + H_{\rm Rest} \approx \\ \hspace{-0.1cm} \approx \hspace{-0.1cm}4.15 + 0.82+1.62 + 2.0 \approx 8.6\,\, {\rm bit/Silbe} \hspace{0.05cm}.$$
- Nach der Kaeding–Studie von 1898 bilden die 400 häufigsten Stammsilben (beginnend mit „de”) 47% eines deutschen Textes und tragen zur Entropie mit $H_{\text{Stamm}}$ ≈ 4.15 bit/Silbe bei.
- Der Beitrag der 242 häufigsten Vorsilben – an erster Stelle „ge” mit 9% – wird von Küpfmüller mit $H_{\text{Vor}}$ ≈ 0.82 bit/Silbe beziffert.
- Der Beitrag der 118 meistgebrauchten Endsilben ist $H_{\text{End}}$ ≈ 1.62 bit/Silbe. Am häufigsten tritt „en” am Ende eines Wortes mit 30% auf.
- Der Rest von 14% verteilt sich auf bisher nicht erfasste Silben. Küpfmüller nimmt dazu an, dass es davon 4.000 gibt und diese gleichverteilt sind. Er setzt dafür $H_{\text{Rest}}$ ≈ 2 bit/Silbe an.
3.) Für die durchschnittliche Buchstabenzahl je Silbe ermittelte Küpfmüller den Wert 3.03. Daraus schloss er auf die dritte Entropienäherung hinsichtlich der Buchstaben:
$$H_3 \approx \frac{8.6}{3.03}\approx 2.8\,\, {\rm bit/Buchstabe}\hspace{0.05 cm}.$$
Küpfmüllers Abschätzung der Entropienäherung H3 basierte vor allem auf den Silbenhäufigkeiten und dem Mittelwert von 3.03 Buchstaben pro Silbe. Um eine weitere Entropienäherung Hk mit größerem k zu erhalten, analysierte Küpfmüller zusätzlich die Wörter in deutschen Texten. Er kam zu folgenden Ergebnissen:
4.) Die 322 häufigsten Wörter liefern einen Entropiebeitrag von 4.5 bit/Wort. Die Beiträge der restlichen 40.000 Wörter wurden geschätzt, wobei angenommen wurde, dass die Häufigkeiten von seltenen Wörtern reziprok zu ihrer Ordnungszahl sind. Mit diesen Voraussetzungen ergibt sich der mittlere Informationsgehalt eines Wortes zu ca. 11 bit.
5.) Die Auszählung ergab im Mittel 5.5 Buchstaben pro Wort. Analog zu Punkt (3) wurde so die Entropienäherung für $k$ = 5.5 angenähert:
$$H_{5.5} \approx \frac{11}{5.5}\approx 2\,\, {\rm bit/Buchstabe}\hspace{0.05 cm}.$$
Natürlich kann $k$ gemäß Definition nur ganzzahlige Werte annehmen. Diese Gleichung ist deshalb so zu interpretieren, dass sich für $H_5$ ein etwas größerer und für $H_6$ ein etwas kleinerer Wert ergeben wird.
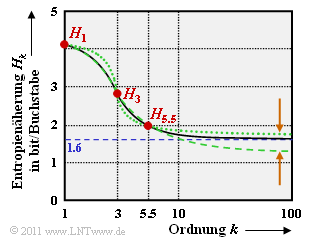
6.) Man kann nun versuchen, aus diesen drei Punkten durch Extrapolation den Endwert der Entropie für $k$ → ∞ zu ermitteln. In folgender Grafik wird dies bei logarithmisch aufgetragener Abszisse versucht:
Die durchgehende Linie ist der Originalarbeit von Küpfmüller [Küp54] entnommen und führt zum Endwert $H$ = 1.6 bit/Buchstabe. Die grünen Kurven (vom LNTwww–Autor hinzugefügt) und die braunen Pfeile zeigen aber, dass eine solche Extrapolation nur sehr vage ist.
7.) Küpfmüller versuchte anschließend, den von ihm gefundenen Endwert $H$ = 1.6 bit/Buchstabe mit völlig anderer Methodik – siehe nächster Abschnitt – zu verifizieren. Nach dieser Abschätzung revidierte er sein Ergebnis geringfügig auf $H$ = 1.51 bit/Buchstabe.
8.) Shannon hatte drei Jahre vorher nach völlig anderer Vorgehensweise für die englische Sprache den Entropiewert $H$ ≈ 1 bit/Buchstabe angegeben, allerdings unter Berücksichtigung des Leerzeichens. Um seine Ergebnisse mit Shannom vergleichen zu können, hat Küpfmüller das Leerzeichen nachträglich in sein Ergebnis eingerechnet:
$$H =1.51 \cdot \frac{5.5}{6.5}\approx 1.3\,\, {\rm bit/Buchstabe}\hspace{0.05 cm}.$$
Der Korrekturfaktor ist der Quotient aus der mittleren Wortlänge ohne Berücksichtigung des Leerzeichens (5.5) und der mittleren Wortlänge mit Berücksichtigung des Leerzeichens (6.5).
Der Vollständigkeit halber seien hier noch Küpfmüllers Überlegungen dargelegt, die ihn zum Endergebnis $H$ = 1.51 bit/Buchstabe führten. Da es für die Statistik von Wortgruppen oder ganzen Sätzen keine Unterlagen gab, schätzte er den Entropiewert der deutschen Sprache wie folgt ab:
- Ein beliebiger zusammenhängender deutscher Text wird hinter einem bestimmten Wort abgedeckt. Der vorhergehende Text wird gelesen, und der Leser soll versuchen, das folgende Wort aus dem Zusammenhang mit dem vorhergehenden Text zu ermitteln.
- Bei sehr vielen solcher Versuche ergibt die prozentuale Zahl der Treffer ein Maß für die Bindungen zwischen Wörtern und Sätzen. Es zeigt sich, dass bei ein und derselben Textart (Romane, wissenschaftliche Schriften, usw.) ein und desselben Autors relativ schnell (etwa 100 bis 200 Versuche) ein konstanter Endwert dieses Trefferverhältnisses erreicht wird.
- Das Trefferverhältnis hängt aber ziemlich stark von der Art des Textes ab. Für verschiedene Texte ergeben sich Werte zwischen 15% und 33%, mit dem Mittelwert bei 22%. Das heißt aber auch: Im Durchschnitt können 22% der Wörter in einem deutschen Text aus dem Zusammenhang heraus ermittelt werden.
- Anders ausgedrückt: Die Zahl der Wörter eines langen Textes kann mit dem Faktor 0.78 reduziert werden, ohne dass der Nachrichtengehalt des Textes eine signifikante Einbuße erfährt. Ausgehend vom Bezugswert $H_{5.5}$ = 2 bit/Buchstabe (siehe Punkt (5), letzte Seite) für ein mittellanges Wort ergibt sich somit die Entropie $H$ ≈ 0.78 · 2 = 1.56 bit/Buchstabe.
- Küpfmüller überprüfte diesen Wert mit einer vergleichbaren empirischen Untersuchung der Silben und ermittelte den Reduktionsfaktor 0.54 hinsichtlich Silben. Als Endergebnis nennt Küpfmüller $H$ = 0.54 · $H_3$ ≈ 1.51 bit/Buchstabe, wobei $H_3$ ≈ 2.8 bit/Buchstabe der Entropie einer Silbe mittlerer Länge (≈ 3 Buchstaben, siehe Punkt (3), vorletzte Seite) entspricht.
Die vielleicht als zu kritisch empfundenen Bemerkungen auf dieser Seite sollen die Bedeutung von Küpfmüllers Entropieabschätzung nicht herabsetzen, eben so wenig wie Shannon's Beiträge zur gleichen Thematik. Sie sollen nur auf die großen Schwierigkeiten hinweisen, die bei dieser Aufgabenstellung auftreten. Dies ist vielleicht auch der Grund dafür, dass sich seit den 1950er Jahren niemand mehr mit dieser Problematik intensiv beschäftigt hat.
Einige eigene Simulationsergebnisse
Die Angaben von Karl Küpfmüller hinsichtlich der Entropie der deutschen Sprache sollen nun mit einigen Simulationsergebnissen verglichen werden, die vom Autor G. Söder dieses Kapitels am Lehrstuhl für Nachrichtentechnik der Technischen Universität München gewonnen wurden. Die Resultate basieren auf
- dem Programm WDIT (Wertdiskrete Informationstheorie) aus dem Praktikum [Söd01]; der Link weist auf die Zip–Version des Programms,
- einer ASCII–Version der deutschen Bibel mit fast N = 4.37 Millionen Schriftzeichen, die auf den Symbolumfang M = 33 reduziert wurde:
a, b, c, ... , x, y, z, ä, ö, ü, ß, LZ, ZI, IP.
Nicht unterschieden wurde bei unserer Analyse zwischen Groß– und Kleinbuchstaben. Gegenüber Küpfmüllers Analyse wurden hier noch zusätzlich berücksichtigt:
- die deutschen Umlaute „ä”, „ö”, „ü” und „ß”, die etwa 1.2% des Bibeltextes ausmachen,
- die Klasse IP (Interpunktion) mit ca. 3%,
- die Klasse ZI (Ziffer) mit ca. 1.3% in Folge der Vers–Nummerierung,
- das Leerzeichen (LZ) als das häufigste Zeichen (17.8%), noch vor dem „e” (12.8%).
Die nachfolgende Tabelle fasst die Ergebnisse zusammen. N bezeichnet die jeweils analysierte Dateigröße in Schriftzeichen (Byte). Die Interpretation folgt auf der nächsten Seite.
[[File: P_ID2267__Inf_T_1_3_S3.png|Entropiewerte (in bit/Schriftzeichen) der deutschen Bibel]]
Hinweis: Betrachten Sie diese Ergebnisse bitte nicht als Teil einer wissenschaftlichen Untersuchung, sondern nur als den Versuch, Studierenden die in Kapitel 1.3 behandelte Thematik in einem Praktikum näher zu bringen. Als Grundlage dieser Untersuchung wurde von der Bibel ausgegangen, da uns sowohl deren deutsche als auch die englische Fassung im geeigneten ASCII–Format zur Verfügung gestellt wurden.
Die in der Tabelle angegebenen Entropien $H_0$ (Entscheidungsgehalt), $H_1$, $H_2$ und $H_3$ wurden jeweils aus $N$ Schriftzeichen ermittelt und sind jeweils in bit/Schriftzeichen angegeben. Die gesamte Datei „Bibel” (in deutscher Sprache) beinhaltet fast $N$ = 4.37 Millionen Schriftzeichen, was bei 42 Zeilen pro Seite und 80 Zeichen pro Zeile etwa einem Buch mit 1300 Seiten entsprechen würde. Der Symbolumfang ist $M$ = 33. Die Ergebnisse lassen sich wie folgt zusammenfassen:
- In allen Zeilen nehmen die Entropienäherungen $H_k$ mit wachsendem $k$ monoton ab. Der Abfall verläuft konvex, das heißt, es ist $H_1$ – $H_2$ > $H_2$ – $H_3$. Die Extrapolation des Endwertes ( $k$ → ∞ ) ist aus den jeweils ermittelten drei Entropienäherungen nicht (oder nur sehr vage) möglich.
- Verzichtet man auf die Auswertung der Ziffern (ZI, Zeile 2 ⇒ $M$ = 32) und zusätzlich auf die Auswertung der Interpunktionszeichen IP, Zeile 3 ⇒ $M$ = 31), so nehmen die Entropienäherungen $H_1$ (um 0.114), $H_2$ (um 0.063) und $H_3$ (um 0.038) ab. Auf den Endwert $H$ als dem Grenzwert von $H_k$ für $k$ → ∞ wirkt sich der Verzicht auf Ziffern (ZI) und Interpunktion (IP) voraussichtlich kaum aus.
- Lässt man bei der Auswertung noch das Leerzeichen (LZ, Zeile 4 → $M$ = 30) außer Betracht, so ergibt sich nahezu die gleiche Konstellation wie von Küpfmüller ursprünglich betrachtet. Der einzige Unterschied sind die eher seltenen deutschen Sonderzeichen „ä”, „ö”, „ü” und „ß”.
- Der in der letzten Zeile angegebene $H_1$–Wert 4.132 stimmt mit dem von Küpfmüller ermittelten Wert $H_1$ ≈ 4.1 sehr gut überein. Hinsichtlich der $H_3$–Werte gibt es aber deutliche Unterschiede: Unsere Analyse ergibt $H_3$ ≈ 3.4 gegenüber Küpfmüllers 2.8 (alle Angaben in bit/Buchstabe).
- Aus der Auftrittshäufigkeit des Leerzeichens (17.8%) ergibt sich hier eine mittlere Wortlänge von 1/0.178 – 1 ≈ 4.6, ein kleinerer Wert als von Küpfmüller (5.5) angegeben. Die Diskrepanz lässt sich mit unserer Analysedatei „Bibel” erklären (viele Leerzeichen aufgrund der Vers–Nummern).
- Interessant ist der Vergleich der Zeilen 3 und 4. Berücksichtigt man das Leerzeichen, so wird zwar $H_0$ von $\log_2$ (30) auf $\log_2$ (31) vergrößert, aber man verringert dadurch $H_1$ (um den Faktor 0.98), $H_2$ (um 0.96) und $H_3$ (um 0.93). Küpfmüller hat diesen Faktor intuitiv mit 85% berücksichtigt.
Obwohl wir unsere eigenen Recherchen als nicht so bedeutend ansehen, so glauben wir doch, dass für heutige Texte die von Shannon angegebenen 1.0 bit/Buchstabe für die englische Sprache und auch Küpfmüllers 1.3 bit/Buchstabe für Deutsch etwas zu niedrig sind, unter Anderem, weil der Symbolumfang deutlich größer ist, als von Shannon und Küpfmüller bei ihren Analysen berücksichtigt – beispielsweise gilt für den ASCII–Zeichensatz M = 256, die vielfachen Formatierungsmöglichkeiten (Unterstreichungen, Fett- und Kursivschrift, Einrückungen, Farben) den Informationsgehalt eines Dokuments erhöhen.
Synthetisch erzeugte Texte
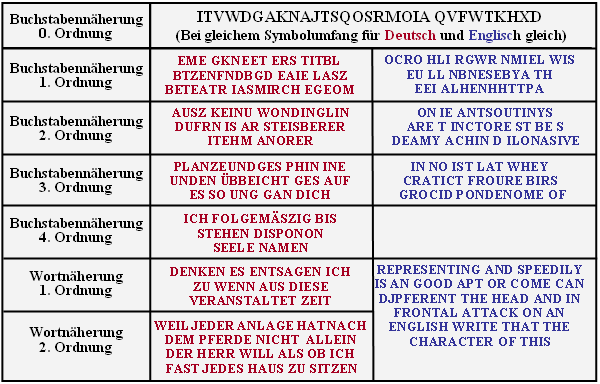
In der Grafik sind künstlich erzeugte deutsche und englische Texte angegeben, die [1] entnommen wurden. Der zugrundeliegende Symbolumfang ist M = 27, das heißt, berücksichtigt sind alle Buchstaben (ohne Umlaute und „ß”) sowie das Leerzeichen.
- Die Buchstabennäherung nullter Ordnung geht von gleichwahrscheinlichen Zeichen aus. Hier ist kein Unterschied zwischen Deutsch (rot) und Englisch (blau) festzustellen.
- Bei der ersten Buchstabennäherung werden bereits die unterschiedlichen Häufigkeiten berücksichtigt, bei den Näherungen höherer Ordnung auch die vorangegangenen Zeichen.
- Bei einer Synthese 4. Ordnung ⇒ die Wahrscheinlichkeit für einen neuen Buchstaben hängt von den drei zuletzt ausgewählten Zeichen ab – erkennt man bereits sinnhafte Worte.
- Die Wortnäherung 1. Ordnung synthetisiert Sätze gemäß den Wortwahrscheinlichkeiten, die Näherung 2. Ordnung berücksichtigt zusätzlich noch das vorherige Wort.
Weitere Information zur synthetischen Erzeugung von deutschen und englischen Texten finden Sie in Aufgabe A1.8.
Aufgaben zu Kapitel 1.3
Quellenverzeichnis
</references>
- ↑ Küpfmüller, K.: Die Entropie der deutschen Sprache. Fernmeldetechnische Zeitung 7, 1954, S. 265-272.