Difference between revisions of "Aufgaben:Exercise 3.6: Partitioning Inequality"
| Line 26: | Line 26: | ||
$D(P_X^{ (A) } \parallel Q_X^{ (A) } ) \leq D(P_X \parallel Q_X)$ | $D(P_X^{ (A) } \parallel Q_X^{ (A) } ) \leq D(P_X \parallel Q_X)$ | ||
| + | |||
| + | |||
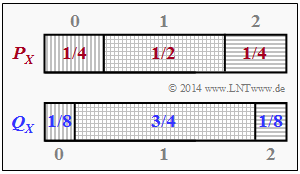
| + | In der Aufgabe (a) soll die Kullback–Leibler–Distanz der beiden Wahrscheinlichkietsfunktionen $P_X(X)$ und $Q_X(X)$ für $X = \{0, 1, 2\} \Rightarrow |X| = 3$ ermittelt werden. Anschließend soll die Menge $X$ entsprechend | ||
| + | :* $A = \{A_1 , A_2\}$ mit $A_1 =\{0\}$ und $A_2 = \{ 1,2 \}$ , | ||
| + | :* $B = \{B_1 , B_2\}$ mit $B_1 =\{1\}$ und $B_2 = \{ 0,2 \}$ , | ||
| + | :* $C = \{C_1 , C_2\}$ mit $C_1 =\{2\}$ und $C_2 = \{ 0,1\}$ , | ||
| + | |||
| + | mit $K = 2$ partitioniert werden und es sollen die jeweiligen Kullback–Leibler–Distanzen | ||
Revision as of 21:52, 25 November 2016
Die $Kullback–Leibler–Distanz$ (kurz KLD) wird auch in der „Partitionierungsungleichung” (englisch: Partition Unequality) verwendet:
- Wir gehen von der Menge
$$X=\{ x_1,x_2,.....,x_M \}$$ und den Wahrscheinlichkeitsfunktionen
$P_X(X) = P_X(x_1,x_2,....,x_M)$ ,
$Q_X(X) = Q_X(x_1,x_2,....,x_M)$ aus, die in irgendeiner Form „ähnlich” sein sollen
- Die Menge $X$ unterteilen wir in die Partitionen $A_1, ..., A_K$ , die zueinander disjunkt sind und ein $vollständiges System$ ergeben:
$\bigcup_{i=_1}^K A_i = X$ , $A_i \cap A_j = \phi$ für $1 \leq i \neq j \leq K$
- Die Wahrscheinlichkeitsfunktionen bezüglich der Partitionierungen $A=\{ A_1,A_2,.....,A_K \}$bezeichnen wir im Folgenden mit
$P_X^{ (A) } = [ P_X(A_1),.......,P_X(A_K)]$ , wobei $P_X(A_i) = \sum\limits_{ x \epsilon A_i } P_X(x)$
$Q_X^{ (A) } = [ Q_X(A_1),.......,Q_X(A_K)]$ , wobei $Q_X(A_i) = \sum\limits_{ x \epsilon A_i } Q_X(x)$
Die $Partitionierungsungleichung$ liefert folgende Größenrelation hinsichtlich der Kullback–Leibler–Distanzen:
$D(P_X^{ (A) } \parallel Q_X^{ (A) } ) \leq D(P_X \parallel Q_X)$
In der Aufgabe (a) soll die Kullback–Leibler–Distanz der beiden Wahrscheinlichkietsfunktionen $P_X(X)$ und $Q_X(X)$ für $X = \{0, 1, 2\} \Rightarrow |X| = 3$ ermittelt werden. Anschließend soll die Menge $X$ entsprechend
- $A = \{A_1 , A_2\}$ mit $A_1 =\{0\}$ und $A_2 = \{ 1,2 \}$ ,
- $B = \{B_1 , B_2\}$ mit $B_1 =\{1\}$ und $B_2 = \{ 0,2 \}$ ,
- $C = \{C_1 , C_2\}$ mit $C_1 =\{2\}$ und $C_2 = \{ 0,1\}$ ,
mit $K = 2$ partitioniert werden und es sollen die jeweiligen Kullback–Leibler–Distanzen
Fragebogen
Musterlösung