Difference between revisions of "Aufgaben:Exercise 3.7: Some Entropy Calculations"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Verschiedene Entropien zweidimensionaler Zufallsgrößen }} [[File:|right|]] ===Fragebogen=== <quiz display=s…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2766__Inf_A_3_6.png|right|]] |
| + | Wir betrachten die beiden Zufallsgrößen $XY$ und $UV$ mit den folgenden 2D-Wahrscheinlichkeitsfunktionen: | ||
| + | |||
| + | $$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$, | ||
| + | |||
| + | $$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$. | ||
| + | |||
| + | Für die Zufallsgröße $XY$sollen in dieser Aufgabe berechnet werden: | ||
| + | |||
| + | :* die Verbundentropie (englisch: Joint Entropy): | ||
| + | |||
| + | $H(XY) = -E[log_2 P_{ XY }( X,Y)]$ | ||
| + | :* die beiden Einzelentropien: | ||
| + | |||
| + | $$H(X) = -E[log_2 P_X( X)]$$ | ||
| + | $$H(Y) = -E[log_2 P_Y( Y)]$$ | ||
Revision as of 14:38, 26 November 2016
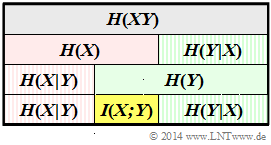
Wir betrachten die beiden Zufallsgrößen $XY$ und $UV$ mit den folgenden 2D-Wahrscheinlichkeitsfunktionen:
$$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$,
$$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$.
Für die Zufallsgröße $XY$sollen in dieser Aufgabe berechnet werden:
- die Verbundentropie (englisch: Joint Entropy):
$H(XY) = -E[log_2 P_{ XY }( X,Y)]$
- die beiden Einzelentropien:
$$H(X) = -E[log_2 P_X( X)]$$ $$H(Y) = -E[log_2 P_Y( Y)]$$
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.