Aufgaben:Exercise 3.9: Conditional Mutual Information

• Return to book

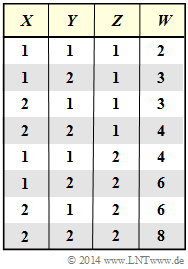
Wir gehen von den statistisch unabhängigen Zufallsgrößen $X$, $Y$ und $Z$mit den folgenden Eigenschaften aus :

$X \epsilon \{1,2\}$ , $Y \epsilon \{1,2\}$ , $Z \epsilon \{1,2\}$

$P_X(X) = P_Y(Y) = [ 1/2 , 1/2]$ , $P_Z(Z) = [ p, 1-p]$.

Aus $X$, $Y$ und $Z$ bilden wir die neue Zufallsgröße

$W = (X+Y). Z$.

Damit ist offensichtlich, dass es zwischen den beiden Zufallsgrößen $X$und W statistische Abhängigkeiten gibt, die sich auch in der Transinformation $I(X; W) ≠ 0$ zeigen werden.

Außerdem wird auch $I(Y; W) ≠ 04 sowie $I(Z; W) ≠ 04 gelten, worauf in dieser Aufgabe jedoch nicht näher eingegangen wird.

In dieser Aufgabe werden drei verschiedene Transinformationsdefinitionen verwendet:

• die herkömmliche Transinformation zwischen $X$ und $W$:

$I(X;W) = H(X) - H(X \mid W)$ ,

• die bedingte Transinformation zwischen $X$ und $W$ bei gegebenem Festwert $Z = z$:

$I(X;W \mid Z=z) = H(X \mid Z=z) - H(X \mid W , Z=z)$,

• die bedingte Transinformation zwischen $X$ und $W$ bei gegebener Zufallsgröße $Z$:

$I(X;W \mid Z) = H(X \mid Z) - H(X \mid W Z)$.

Der Zusammenhang zwischen den beiden letzten Definitionen lautet:

$I(X;W \mid Z) = \sum\limits_{z \epsilon supp(P_Z)} P_Z(Z) . I(X; W \mid Z=z)$.

Hinwies: Die Aufgabe gehört zum Themengebiet von Kapitel 3.2.

Fragebogen

1

Wie groß ist die Transinformation zwischen $X$ und $W$, falls stets $Z = 1$ gilt?

$ I(X; W | Z = 1)$ = $bit$

2

Wie groß ist die Transinformation zwischen $X$ und $W$, falls stets $Z = 2$ gilt?

$ I(X; W | Z = 2)$ = $bit$

3

Nun gelte $p = Pr(Z = 1)$. Wie groß ist die bedingte Transinformation zwischen $X$ und $W$ unter der Annahme, dass $z \epsilon Z = {1, 2}$ bekannt ist?

$ p = 1/2: I(X; W | Z)$ = $bit$

$ p = 3/4: I(X; W | Z)$ = $bit$

4

Wie groß ist die unkonditionierte Transinformation?

$p = 1/2: I(X; W)$ = $bit$

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.