Difference between revisions of "Aufgaben:Exercise 3.11: Erasure Channel"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Anwendung auf die Digitalsignalübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multi…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2791__Inf_A_3_10.png|right|]] |
| + | Betrachtet wird ein Auslöschungskanal mit | ||
| + | :* den M Eingängen $x ∈ X = \{1, 2, ... , M\}$, und | ||
| + | :* den $M + 1$ Ausgängen $y ∈ Y = \{1, 2, ... , M, E\}$ | ||
| + | |||
| + | Die Grafik zeigt das Modell für den Sonderfall $M = 4$. Das Sinkensymbol $y = E$ berücksichtigt eine Auslöschung (englisch: Erasure) für den Fall, dass der Empfänger keine hinreichend gesicherte Entscheidung treffen kann | ||
| + | |||
| + | Die Übergangswahrscheinlichkeiten sind für $1 ≤ μ ≤ M$ wie folgt gegeben: | ||
| + | $${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) \hspace{-0.15cm} = \hspace{-0.15cm} 1-\lambda \hspace{0.05cm}$$ | ||
| + | $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) \hspace{-0.15cm} =\hspace{-0.15cm} \lambda \hspace{0.05cm}$$ | ||
| + | Gesucht ist | ||
| + | :* die Kapazität $C_{M–EC}$ dieses ''M–ary Erasure Channels'', | ||
| + | :* die Kapazität $C_{BEC}$ des Binary Erasure Channels als Sonderfall des obigen Modells, | ||
| + | '''Hinweis:''' Die Aufgabe beschreibt die Thematik von [http://en.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3]. In dem obigen Schaubild sind Auslöschungen (Wahrscheinlichkeit $λ$) blau gezeichnet und „richtige Übertragungswege” (also von $X = μ$ nach $Y = μ$) blau ($1 ≤ μ ≤ M$). | ||
| Line 9: | Line 22: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | { Welches $P_X(X)$ ist zur Kanalkapazitätsberechnung allgemein anzusetzen? |
|type="[]"} | |type="[]"} | ||
- Falsch | - Falsch | ||
Revision as of 15:21, 28 November 2016
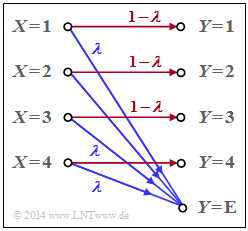
Betrachtet wird ein Auslöschungskanal mit
- den M Eingängen $x ∈ X = \{1, 2, ... , M\}$, und
- den $M + 1$ Ausgängen $y ∈ Y = \{1, 2, ... , M, E\}$
Die Grafik zeigt das Modell für den Sonderfall $M = 4$. Das Sinkensymbol $y = E$ berücksichtigt eine Auslöschung (englisch: Erasure) für den Fall, dass der Empfänger keine hinreichend gesicherte Entscheidung treffen kann
Die Übergangswahrscheinlichkeiten sind für $1 ≤ μ ≤ M$ wie folgt gegeben: $${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) \hspace{-0.15cm} = \hspace{-0.15cm} 1-\lambda \hspace{0.05cm}$$ $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) \hspace{-0.15cm} =\hspace{-0.15cm} \lambda \hspace{0.05cm}$$ Gesucht ist
- die Kapazität $C_{M–EC}$ dieses M–ary Erasure Channels,
- die Kapazität $C_{BEC}$ des Binary Erasure Channels als Sonderfall des obigen Modells,
Hinweis: Die Aufgabe beschreibt die Thematik von Kapitel 3.3. In dem obigen Schaubild sind Auslöschungen (Wahrscheinlichkeit $λ$) blau gezeichnet und „richtige Übertragungswege” (also von $X = μ$ nach $Y = μ$) blau ($1 ≤ μ ≤ M$).
Fragebogen
Musterlösung