Difference between revisions of "Aufgaben:Exercise 3.15: Data Processing Theorem"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Anwendung auf die Digitalsignalübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multi…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2818__Inf_A_3_14.png|right|]] |
| − | + | Wir betrachten die folgende Datenverarbeitungskette: | |
| + | :* Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ verarbeitet, der durch bedingte Wahrscheinlichkeiten $(P_Y|X)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$. | ||
| + | :* Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z|Y} $gegeben. $Z$ hängt allein von $Y$ ab (entweder deterministisch oder stochastisch) und ist unabhängig von $X$: | ||
| + | $$P_{Z\hspace{0.01cm}|\hspace{0.01cm} XY\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} x, y) =P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ | ||
| + | Hierbei wurde folgende Nomenklatur benutzt: | ||
| + | $$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ | ||
| + | Die Verbund–Wahrscheinlichkeitsfunktion (englisch: ''Joint Probability Mass Function'') lautet: | ||
| + | $$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.01cm}|\hspace{0.01cm} X\hspace{-0.03cm}}(y\hspace{0.01cm}|\hspace{0.01cm} x)\cdot P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ | ||
| + | Das bedeutet auch: $X → Y → Z$ bilden eine [http://en.lntwww.de/Stochastische_Signaltheorie/Markovketten Markovkette]. Für eine solche gilt das Data Processing Theorem mit folgender Konsequenz: | ||
| + | $$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm}I(X;Y ) \hspace{0.05cm},\\ I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm} I(Y;Z ) \hspace{0.05cm}.$$ | ||
| + | Das Theorem besagt somit: | ||
| + | :* Man kann durch Manipulation (''Processing'') der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen. | ||
| + | :* Datenverarbeitung (durch den Prozessor 2) dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen. | ||
| + | '''Hinweis:''' Die Aufgabe gehört zu [http://en.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie lässt sich das Ergebnis $I(X; Y) = 1 – H_{bin}(p)$ herleiten? |
|type="[]"} | |type="[]"} | ||
| − | - | + | + Über die Eigenschaften eines streng symmetrischen Kanals. |
| − | + | - Weil $H_{bin}(p)$ eine konkave Funktion ist. | |
| + | - Das Ergebnis gilt für jede Wahrscheinlichkeitsfunktion $P_X(X).$ | ||
| − | { | + | {Welche Transinformation ergibt sich für den Prozessor $1$ mit $p = 0.1$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p = 0.1: I(X; Y)$ = { 0.531 3% } $bit$ |
| + | {Welche Transinformation ergibt sich für den Prozessor 2 mit $q = 0.2$? | ||
| + | |type="{}"} | ||
| + | $q = 0.2: I(Y; Z)$ = { 0.278 3% } $bit$ | ||
| + | {Welche Transinformation ergibt sich für das Gesamtsystem? | ||
| + | |type="{}"} | ||
| + | $p = 0.1, q = 0.2: I(X; Z)$ = { 0.173 3% } $bit$ | ||
| + | {Erfüllt dieses Beispiel das Data Processing Theorem? | ||
| + | |type="[]"} | ||
| + | + ja | ||
| + | - nein | ||
</quiz> | </quiz> | ||
Revision as of 23:49, 28 November 2016
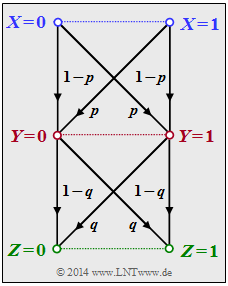
Wir betrachten die folgende Datenverarbeitungskette:
- Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ verarbeitet, der durch bedingte Wahrscheinlichkeiten $(P_Y|X)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$.
- Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z|Y} $gegeben. $Z$ hängt allein von $Y$ ab (entweder deterministisch oder stochastisch) und ist unabhängig von $X$:
$$P_{Z\hspace{0.01cm}|\hspace{0.01cm} XY\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} x, y) =P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ Hierbei wurde folgende Nomenklatur benutzt: $$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ Die Verbund–Wahrscheinlichkeitsfunktion (englisch: Joint Probability Mass Function) lautet: $$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.01cm}|\hspace{0.01cm} X\hspace{-0.03cm}}(y\hspace{0.01cm}|\hspace{0.01cm} x)\cdot P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ Das bedeutet auch: $X → Y → Z$ bilden eine Markovkette. Für eine solche gilt das Data Processing Theorem mit folgender Konsequenz: $$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm}I(X;Y ) \hspace{0.05cm},\\ I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm} I(Y;Z ) \hspace{0.05cm}.$$ Das Theorem besagt somit:
- Man kann durch Manipulation (Processing) der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
- Datenverarbeitung (durch den Prozessor 2) dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.
Hinweis: Die Aufgabe gehört zu Kapitel 3.3.
Fragebogen
Musterlösung