Difference between revisions of "Aufgaben:Exercise 1.2: Entropy of Ternary Sources"
From LNTwww
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File: | + | [[File:Inf_A_1_2_vers2.png|right|Wahrscheinlichkeiten zweier Ternärquellen]] |
| − | + | Die Entropie einer wertdiskreten gedächtnislosen Nachrichtenquelle mit $M$ möglichen Symbolen lautet: | |
:$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} | :$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} | ||
{\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ | {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ | ||
| − | + | Hierbei bezeichnen die $p_\mu$ die Auftrittswahrscheinlichkeiten der einzelnen Symbole bzw. Ereignisse. Im vorliegenden Beispiel werden die Ereignisse mit <b>R</b>(ot), <b>G</b>(rün) und <b>S</b>(chwarz) bezeichnet. | |
| − | + | *Bei einer binären Quelle mit den Auftrittswahrscheinlichkeiten $p$ und $1-p$ kann hierfür geschrieben werden: | |
:$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot | :$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot | ||
| − | {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm}.$$ | + | {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} |
| − | + | {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ | |
| + | *Die Entropie einer mehrstufigen Quelle lässt sich häufig mit dieser „binären Entropiefunktion” $H_{\rm bin}(p)$ ausdrücken. | ||
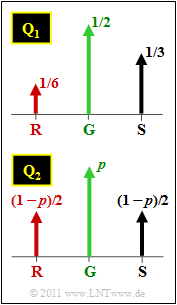
| − | + | Betrachtet werden in dieser Aufgabe zwei Ternärquellen mit den Symbolwahrscheinlichkeiten gemäß der obigen Grafik: | |
| − | + | * die Quelle $\rm Q_1$ mit $p_{\rm G }= 1/2$, $p_{\rm S }= 1/3$ und $p_{\rm R }= 1/6$, | |
| + | * die Quelle $\rm Q_2$ mit $p_{\rm G }= p$ sowie $p_{\rm S } = p_{\rm R } = (1-p)/2$. | ||
| − | |||
| − | + | Die Ternärquelle $\rm Q_2$ lässt sich auch auf das Roulette anwenden, wenn ein Spieler nur auf die Felder <b>R</b>ot, <b>S</b>chwarz und <b>G</b>rün (die „Null”) setzt. Dieser Spieltyp wird im Fragebogen mit „Roulette 1” bezeichnet. | |
| − | + | Dagegen weist „Roulette 2” darauf hin, dass der Spieler auf einzelne Zahlen (<b>0</b>, ... , <b>36</b>) setzt. | |
| − | : | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Gedächtnislose_Nachrichtenquellen|Gedächtnislose Nachrichtenquellen]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 30: | Line 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Entropie | + | {Welche Entropie $H$ besitzt die Quelle $\rm Q_1$? |
|type="{}"} | |type="{}"} | ||
| − | $Q_1: | + | $\rm Q_1$: $H \ = $ { 1.46 3% } $\ \rm bit$ |
| − | {Welche der folgenden Aussagen sind zutreffend, wenn man <b>R</b>, <b>G</b> und <b>S</b> durch die Zahlenwerte | + | {Welche der folgenden Aussagen sind zutreffend, wenn man <b>R</b>, <b>G</b> und <b>S</b> durch die Zahlenwerte $-1$, $0$ und $+1$ darstellt? |
|type="[]"} | |type="[]"} | ||
- Es ergibt sich eine kleinere Entropie. | - Es ergibt sich eine kleinere Entropie. | ||
| Line 42: | Line 45: | ||
| − | {Bestimmen Sie die Entropie der Quelle | + | {Bestimmen Sie die Entropie der Quelle $\rm Q_2$ unter Verwendung der binären Entropiefunktion $H_{\rm bin}(p)$. Welcher Wert ergibt sich für $p = 0.5$? |
|type="{}"} | |type="{}"} | ||
| − | $Q_2 | + | ${\rm Q_2}, \ p = 0.5$: $H \ = $ { 1.5 3% } $\ \rm bit$ |
| − | {Für welchen | + | {Für welchen $p$–Wert ergibt sich die maximale Entropie der Quelle $\rm Q_2$? |
|type="{}"} | |type="{}"} | ||
| − | $Q_2,\ H → H_\text{max}:\ | + | ${\rm Q_2},\ H → H_\text{max}$: $p \ = $ { 0.333 3% } |
{Welche Entropie hat die Nachrichtenquelle „Roulette” hinsichtlich der Ereignisse <b>R</b>ot, <b>S</b>chwarz und <b>G</b>rün (die „Null”)? | {Welche Entropie hat die Nachrichtenquelle „Roulette” hinsichtlich der Ereignisse <b>R</b>ot, <b>S</b>chwarz und <b>G</b>rün (die „Null”)? | ||
|type="{}"} | |type="{}"} | ||
| − | $Roulette | + | $\text{Roulette 1}$: $H \ = $ { 1.152 3% } $\ \rm bit$ |
| − | {Welche Entropie weist „Roulette” hinsichtlich der Zahlen | + | {Welche Entropie weist „Roulette” hinsichtlich der Zahlen $0$, ... , $36$ auf? |
|type="{}"} | |type="{}"} | ||
| − | $Roulette | + | $\text{Roulette 2}$: $H \ = $ { 5.209 3% } $\ \rm bit$ |
Revision as of 16:51, 25 April 2017
Die Entropie einer wertdiskreten gedächtnislosen Nachrichtenquelle mit $M$ möglichen Symbolen lautet:
- $$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$
Hierbei bezeichnen die $p_\mu$ die Auftrittswahrscheinlichkeiten der einzelnen Symbole bzw. Ereignisse. Im vorliegenden Beispiel werden die Ereignisse mit R(ot), G(rün) und S(chwarz) bezeichnet.
- Bei einer binären Quelle mit den Auftrittswahrscheinlichkeiten $p$ und $1-p$ kann hierfür geschrieben werden:
- $$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} {\rm Pseudoeinheit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$
- Die Entropie einer mehrstufigen Quelle lässt sich häufig mit dieser „binären Entropiefunktion” $H_{\rm bin}(p)$ ausdrücken.
Betrachtet werden in dieser Aufgabe zwei Ternärquellen mit den Symbolwahrscheinlichkeiten gemäß der obigen Grafik:
- die Quelle $\rm Q_1$ mit $p_{\rm G }= 1/2$, $p_{\rm S }= 1/3$ und $p_{\rm R }= 1/6$,
- die Quelle $\rm Q_2$ mit $p_{\rm G }= p$ sowie $p_{\rm S } = p_{\rm R } = (1-p)/2$.
Die Ternärquelle $\rm Q_2$ lässt sich auch auf das Roulette anwenden, wenn ein Spieler nur auf die Felder Rot, Schwarz und Grün (die „Null”) setzt. Dieser Spieltyp wird im Fragebogen mit „Roulette 1” bezeichnet.
Dagegen weist „Roulette 2” darauf hin, dass der Spieler auf einzelne Zahlen (0, ... , 36) setzt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Gedächtnislose Nachrichtenquellen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- 2. Mit den Auftrittswahrscheinlichkeiten 1/2, 1/3 und 1/6 erhält man folgenden Entropiewert:
- $$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =\\ \hspace{0.1cm} = \hspace{0.1cm} (1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) =\\ \hspace{0.1cm} = \hspace{0.1cm} 2/3 \cdot 1\,{\rm bit} + 1/2 \cdot 1.585\,{\rm bit}\hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$
- 2. Richtig ist Lösungsvorschlag 2. Die Entropie hängt nur von den Auftrittswahrscheinlichkeiten ab. Es ist dabei egal, welche Zahlenwerte oder physikalische Größen man den einzelnen Symbolen zuordnet. Anders ist es bei Mittelwerten oder der AKF–Berechnung. Werden nur Symbole angegeben, so kann man hierfür keine Momente angeben. Außerdem hängen die Mittelwerte, Autokorrelation, usw. davon ab, ob man die Zuordnung bipolar (–1, 0, +1) oder unipolar (zum Beispiel: 0, 1, 2) vereinbart.
- 3. Die Entropie der Quelle Q2 lässt sich wie folgt ausdrücken:
- $$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}=\\ \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$
- Für p = 0.5 ⇒ Hbin(p) = 1 ergibt sich H = 1.5 bit.
- 4. Die maximale Entropie einer gedächtnislosen Quelle mit dem Symbolumfang M ergibt sich, wenn alle M Symbole gleichwahrscheinlich sind. Für den Sonderfall M = 3 folgt daraus:
- $$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {p = 1/3}\hspace{0.05cm}.$$
- Damit erhält man mit dem Ergebnis der Teilaufgabe (3) die folgende Entropie:
- $$H \hspace{0.1cm} = \hspace{0.1cm} H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 =\\ \hspace{0.1cm} = \hspace{0.1cm} 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} \hspace{0.05cm}.$$
- 5. „Roulette 1” ist informationstheoretisch gleich der Konfiguration Q2 mit p = 1/37:
- $$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$
- Damit erhält man mit dem Ergebnis der Teilaufgabe (3):
- $$H \hspace{0.1cm} = \hspace{0.1cm} H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} =\\ \hspace{0.1cm} = \hspace{0.1cm} {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} \hspace{0.05cm}.$$
- 6. Setzt man bei Roulette auf einzelne Zahlen ⇒ Konfiguration „Roulette 2”, so sind alle Zahlen von 0 bis 36 gleichwahrscheinlich und man erhält:
- $$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} \hspace{0.05cm}.$$