Difference between revisions of "Aufgaben:Exercise 2.11: Arithmetic Coding"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2468__Inf_A_2_11.png|right|]] | + | [[File:P_ID2468__Inf_A_2_11.png|right|Intervallschachtelung bei arithmetischer Codierung]] |
| − | Die arithmetische Codierung ist eine spezielle Form der Entropiecodierung: Auch hier müssen die Symbolwahrscheinlichkeiten bekannt sein. In dieser Aufgabe gehen wir von | + | Die arithmetische Codierung ist eine spezielle Form der Entropiecodierung: Auch hier müssen die Symbolwahrscheinlichkeiten bekannt sein. In dieser Aufgabe gehen wir von $M = 3$ Symbolen aus, die wir mit <b>X</b>, <b>Y</b>, <b>Z</b> benennen. |
| − | + | Während die Huffman–Codierung symbolweise erfolgt, wird bei der Arithmetischen Codierung (AC) eine Symbolfolge der Länge $N$ gemeinsam codiert. Das Codierergebnis ist ein reeller Zahlenwert $r$ aus dem Intervall | |
:$$I = [B, E) = [B, B +{\it \Delta} )\hspace{0.05cm}.$$ | :$$I = [B, E) = [B, B +{\it \Delta} )\hspace{0.05cm}.$$ | ||
Diese Notation bedeutet: | Diese Notation bedeutet: | ||
| + | * Der Beginn $B$ gehört zum Intervall $I$. | ||
| + | * Das Ende $E$ ist nicht mehr in $I$ enthalten. | ||
| + | * Die Intervallbreite ist ${\it} \Delta = E - B$. | ||
| − | :* Der | + | Von den unendlich vielen möglichen Werten $r \in I$ (da $r$ reellwertig ist, also kein Integer) wird derjenige Zahlenwert ausgewählt, der mit der geringsten Bitanzahl auskommt. Hierzu zwei Beispiele zur Verdeutlichung: |
| + | * Der Dezimalwert $r = 3/4$ lässt sich mit zwei Bit darstellen: | ||
| + | :$$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm}\text{binär:}\hspace{0.15cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text | ||
| + | {Code:} \hspace{0.15cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$ | ||
| − | + | * Der Dezimalwert $r = 1/3$ benötigt dagegen unendlich viele Bit: | |
| + | :$$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}... \$$ | ||
| + | :$$ | ||
| + | \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.15cm}0.011101\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| + | \text{Code:} \hspace{0.15cm} \boldsymbol{\rm 011101} \hspace{0.05cm}. $$ | ||
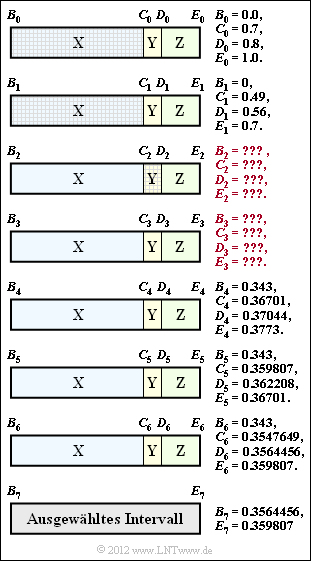
| − | + | In dieser Aufgabe beschränken wir uns auf die Bestimmung des aktuellen Intervalls $I$, gekennzeichnet durch den Beginn $B$ sowie dem Ende $E$ bzw. der Breite $\Delta$. Diese Bestimmung geschieht entsprechend der Intervallschachtelung in obiger Grafik. An der Schraffierung ist zu erkennen, dass die Folge mit den Ternärsymbolen <b>XXY</b> beginnt. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In dieser Aufgabe beschränken wir uns auf die Bestimmung des aktuellen Intervalls | ||
Der Algorithmus funktioniert wie folgt: | Der Algorithmus funktioniert wie folgt: | ||
| + | * Vor Beginn (quasi beim nullten Symbol) wird der gesamte Wahrscheinlichkeitsbereich nach den Wahrscheinlichkeiten $p_{\rm X}$, $p_{\rm Y}$ und $p_{\rm Z}$ in drei Bereiche unterteilt. Die Grenzen liegen bei | ||
| + | :$$B_0 = 0\hspace{0.05cm},\hspace{0.2cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.2cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.2cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$ | ||
| − | + | * Das erste Symbol der zu codierenden Folge ist <b>X</b> ⇒ das ausgewählte Intervall wird durch $B_0$ und $C_0$ begrenzt. Dieses Intervall wird mit neuem Beginn $B_1 = B_0$ und neuem Ende $E_1 = C_0$ in gleicher Weise aufgeteilt wie der Gesamtbereich im nullten Schritt. Die Zwischenwerte sind $C_1$ und $D_1$. | |
| − | + | * Die weitere Intervall–Aufteilung ist Ihre Aufgabe. Beispielsweise sollen in der Teilaufgabe (2) die Grenzen $B_2$, $C_2$, $D_2$ und $E_2$ für das zweite Symbol <b>X</b> ermittelt werden und in der Teilaufgabe (3) entsprechend die Grenzen $B_3$, $C_3$, $D_3$ und $E_3$ für das dritte Symbol <b>Y</b>. | |
| − | |||
| − | |||
| − | :* Die | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | ||
| + | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Der_Shannon.E2.80.93Fano.E2.80.93Algorithmus|Der Shannon-Fano-Algorithmus]]. | ||
| + | *Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul [[Shannon–Fano– und Huffman–Codierung]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
<b>Hinweis:</b> Die Aufgabe bezieht sich auf die Seite 2a und die Seite 2b in Kapitel 2.4. Die Binärdarstellung des ausgewählten Intervalls wird in Aufgabe A2.12 behandelt. | <b>Hinweis:</b> Die Aufgabe bezieht sich auf die Seite 2a und die Seite 2b in Kapitel 2.4. Die Binärdarstellung des ausgewählten Intervalls wird in Aufgabe A2.12 behandelt. | ||
| Line 95: | Line 96: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID2469__Inf_A_2_11_ML.png|right|]] | + | [[File:P_ID2469__Inf_A_2_11_ML.png|right|Intervallschachtelung mit allen Zahlenwerten]] |
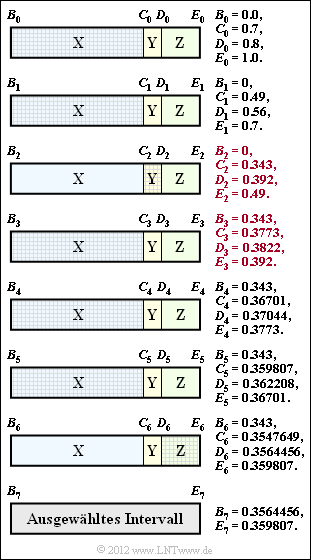
<b>1.</b> Aus der Grafik auf der Angabenseite kann man die Wahrscheinlichkeiten ablesen: | <b>1.</b> Aus der Grafik auf der Angabenseite kann man die Wahrscheinlichkeiten ablesen: | ||
:$$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$ | :$$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$ | ||
Revision as of 14:06, 26 May 2017
Die arithmetische Codierung ist eine spezielle Form der Entropiecodierung: Auch hier müssen die Symbolwahrscheinlichkeiten bekannt sein. In dieser Aufgabe gehen wir von $M = 3$ Symbolen aus, die wir mit X, Y, Z benennen.
Während die Huffman–Codierung symbolweise erfolgt, wird bei der Arithmetischen Codierung (AC) eine Symbolfolge der Länge $N$ gemeinsam codiert. Das Codierergebnis ist ein reeller Zahlenwert $r$ aus dem Intervall
- $$I = [B, E) = [B, B +{\it \Delta} )\hspace{0.05cm}.$$
Diese Notation bedeutet:
- Der Beginn $B$ gehört zum Intervall $I$.
- Das Ende $E$ ist nicht mehr in $I$ enthalten.
- Die Intervallbreite ist ${\it} \Delta = E - B$.
Von den unendlich vielen möglichen Werten $r \in I$ (da $r$ reellwertig ist, also kein Integer) wird derjenige Zahlenwert ausgewählt, der mit der geringsten Bitanzahl auskommt. Hierzu zwei Beispiele zur Verdeutlichung:
- Der Dezimalwert $r = 3/4$ lässt sich mit zwei Bit darstellen:
- $$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\text{binär:}\hspace{0.15cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text {Code:} \hspace{0.15cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$
- Der Dezimalwert $r = 1/3$ benötigt dagegen unendlich viele Bit:
- $$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}... \$$
- $$ \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.15cm}0.011101\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \text{Code:} \hspace{0.15cm} \boldsymbol{\rm 011101} \hspace{0.05cm}. $$
In dieser Aufgabe beschränken wir uns auf die Bestimmung des aktuellen Intervalls $I$, gekennzeichnet durch den Beginn $B$ sowie dem Ende $E$ bzw. der Breite $\Delta$. Diese Bestimmung geschieht entsprechend der Intervallschachtelung in obiger Grafik. An der Schraffierung ist zu erkennen, dass die Folge mit den Ternärsymbolen XXY beginnt.
Der Algorithmus funktioniert wie folgt:
- Vor Beginn (quasi beim nullten Symbol) wird der gesamte Wahrscheinlichkeitsbereich nach den Wahrscheinlichkeiten $p_{\rm X}$, $p_{\rm Y}$ und $p_{\rm Z}$ in drei Bereiche unterteilt. Die Grenzen liegen bei
- $$B_0 = 0\hspace{0.05cm},\hspace{0.2cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.2cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.2cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$
- Das erste Symbol der zu codierenden Folge ist X ⇒ das ausgewählte Intervall wird durch $B_0$ und $C_0$ begrenzt. Dieses Intervall wird mit neuem Beginn $B_1 = B_0$ und neuem Ende $E_1 = C_0$ in gleicher Weise aufgeteilt wie der Gesamtbereich im nullten Schritt. Die Zwischenwerte sind $C_1$ und $D_1$.
- Die weitere Intervall–Aufteilung ist Ihre Aufgabe. Beispielsweise sollen in der Teilaufgabe (2) die Grenzen $B_2$, $C_2$, $D_2$ und $E_2$ für das zweite Symbol X ermittelt werden und in der Teilaufgabe (3) entsprechend die Grenzen $B_3$, $C_3$, $D_3$ und $E_3$ für das dritte Symbol Y.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
- Insbesondere wird Bezug genommen auf die Seite Der Shannon-Fano-Algorithmus.
- Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul Shannon–Fano– und Huffman–Codierung.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Hinweis: Die Aufgabe bezieht sich auf die Seite 2a und die Seite 2b in Kapitel 2.4. Die Binärdarstellung des ausgewählten Intervalls wird in Aufgabe A2.12 behandelt.
Fragebogen
Musterlösung
1. Aus der Grafik auf der Angabenseite kann man die Wahrscheinlichkeiten ablesen:
- $$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$
2. Auch das zweite Symbol ist X. Bei gleichem Vorgehen wie in der Aufgabenbeschreibung erhält man
- $$B_2 \hspace{0.1cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}C_2 = 0.49 \cdot 0.7 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},$$
- $$D_2 \hspace{0.1cm} \underline{= 0.392}\hspace{0.05cm},\hspace{0.2cm}E_2 = C_1 \hspace{0.1cm}\underline{= 0.49} \hspace{0.05cm}.$$
3. Aufgrund von Y als drittes Symbol gelten nun die Begrenzungen B3 = C2 und E3 = D2:
- $$B_3 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm}C_3 \hspace{0.1cm}\underline{= 0.3773}\hspace{0.05cm},$$
- $$D_3 \hspace{0.1cm} \underline{= 0.3822}\hspace{0.05cm},\hspace{0.2cm}E_3 \hspace{0.1cm}\underline{= 0.392} \hspace{0.05cm}.$$
4. Aus B4 = 0.343 = B3 (abzulesen in der Grafik auf dem Angabenblatt) folgt zwingend, dass das vierte zu codierende Quellensymbol ein X war ⇒ Lösungsvorschlag 1.
5. Die Grafik zeigt die Intervallschachtelung mit allen bisherigen Ergebnissen.
- Man erkennt aus der Schraffierung, dass der zweite Lösungsvorschlag die richtige Symbolfolge angibt: XXYXXXZ.
- Die Intervallbreite Δ kann wirklich gemäß dem Lösungsvorschlag 3 ermittelt werden:
- $${\it \Delta} \hspace{0.2cm} = \hspace{0.2cm} 0.359807 - 0.3564456 = 0.003614 \hspace{0.05cm},\\ {\it \Delta} \hspace{0.2cm} = \hspace{0.2cm} p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z} = 0.7^5 \cdot 0.1 \cdot 0.2 = 0.003614 \hspace{0.05cm}. $$
Richtig sind somit die Lösungsvorschläge 2 und 3.
6. Der Vorschlag 1: (0.101100)binär ist auszuschließen, da der zugehörige Dezimalwert r1 > 0.5 ist. Auch der letzte Lösungsvorschlag ist falsch, da (0.001011)binär < (0.01)binär = 0.25dezimal gilt.
Richtig ist der Lösungsvorschlag 2: (0.010111)binär, wegen:
- $$r_2 = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 0 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 1 \cdot 2^{-5} + 1 \cdot 2^{-6} = 0.359375\hspace{0.05cm}. $$