Aufgaben:Exercise 1.3: System Comparison at AWGN Channel

• Return to book

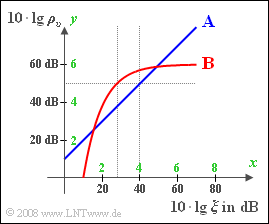
Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten $\text{AWGN}$–Kanal aus und beschreiben folgendes doppelt–logarithmische Diagramm:

• Die Ordinate gibt den Sinken–Störabstand (SNR logarithmiert) $10 · lg ρ_υ$ in dB an.
• Auf der Abszisse ist $10 · lg ξ$ aufgetragen, wobei für die normierte Leistungskenngröße gilt:

$$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$

• In $ξ$ sind also die Sendeleistung $P_S$, der Kanaldämpfungsfaktor $α_K$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst.
• Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden:

$$P_S=5KW , \alpha_k = 0.001 , N_0= 10^{ -10 } \frac{W}{Hz} , B_{NF} = 5 kHz$$ In der Grafik sind zwei Systeme eingezeichnet, deren (x, y)–Verlauf wie folgt beschrieben werden kann:

• System A:

$y = x+1$

• System B:

$$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$ Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung: $$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$ So steht $x = 4$ für $10 · lg ξ = 40$ dB bzw. $ξ = 104$ und $y = 5$ für $10 · lg ρ_υ = 50$ dB, also $ρ_υ = 105$.

Hinweis:Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2.

Fragebogen

1

Welcher Sinken–Störabstand (in dB) ergibt sich bei System A mit $P_S = 5 kW$, $α_K = 0.001$, $N_0 = 10^{ –10 } W/Hz$ und $B_{NF} = 5 kHz$?

$System A: 10 · lg ρ_υ$ = $\text{dB}$

2

Es wird nun $10 · lg ρ_υ ≥ 60$ dB gefordert. Durch welche Maßnahmen (jeweils für sich allein) ist dies zu erreichen?

	Erhöhung der Sendeleistung $P_S$ von $5 kW$ auf $10 kW$.
	Erhöhung des Kanaldämpfungsfaktors $α_K4 von 0.001 auf 0.004.
	Reduzierung der Rauschleistungsdichte $N_0$ auf $10^{ –11 } W/Hz$ .
	Erhöhung der $NF$–Bandbreite von $5 kHz$ auf $6 kHz$.

3

Welcher Störabstand ergibt sich bei System $B$ mit 410 · lg ξ = 40$ dB?

$System B$ : $10 · lg ρ_υ$ = $\text{dB}$

4

Gefordert wird der Störabstand $10 · lg ρ_υ = 50$ dB. Welche Sendeleistung $P_S$ genügt bei System $B$, um diese Qualität zu erzielen?

$P_S$= $\text{ kW }$

5

Für welchen Wert von $10 · lg ξ$ ist die Verbesserung des Systems B gegenüber System A am größten?

$10 · lg ξ$ = $\text{dB}$

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.