Difference between revisions of "Digital Signal Transmission/Optimal Receiver Strategies"
| Line 185: | Line 185: | ||
Bei Vorhandensein solcher Impulsinterferenzen ist die Berechnung der Fehlerwahrscheinlichkeit deutlich schwieriger. Es können jedoch vergleichbare Näherungen wie beim Viterbi–Empfänger angegeben werden, die am Ende von Kapitel 3.8 zu finden sind.<br> | Bei Vorhandensein solcher Impulsinterferenzen ist die Berechnung der Fehlerwahrscheinlichkeit deutlich schwieriger. Es können jedoch vergleichbare Näherungen wie beim Viterbi–Empfänger angegeben werden, die am Ende von Kapitel 3.8 zu finden sind.<br> | ||
| + | == Darstellung des Korrelationsempfängers im Baumdiagramm (3) == | ||
| + | <br> | ||
| + | Bei unipolarer Signalisierung führt eine auf <i>I<sub>i</sub></i> basierende Entscheidung nicht zum richtigen Ergebnis. Hier muss vielmehr auf die korrigierten Vergleichswerte <i>W<sub>i</sub></i> = <i>I<sub>i</sub></i> – <i>E<sub>i</sub></i>/2 zurückgegriffen werden.<br> | ||
| + | [[File:P ID1462 Dig T 3 7 S5c version1.png|Mögliche unipolare Sendesignale für <i>N</i> = 3|class=fit]]<br> | ||
| + | |||
| + | Nachfolgend sehen Sie das Baumdiagramm für den rauschfreien Fall, wobei wie auf der letzten Seite vorausgesetzt ist, dass <i>s</i><sub>5</sub>(<i>t</i>) gesendet wurde. Auch die Farben korrespondieren mit der Grafik auf der letzten Seite.<br> | ||
| + | |||
| + | [[File:P ID1463 Dig T 3 7 S5d version1.png|Baumdiagramm des Korrelationsempfängers (unipolar)|class=fit]]<br> | ||
| + | |||
| + | Für dieses Beispiel ergeben sich folgende Vergleichswerte, jeweils normiert auf <i>E</i><sub>B</sub>: | ||
| + | |||
| + | :<math>I_5 = I_7 = 2, \hspace{0.2cm}I_1 = I_3 = I_4= I_6 = 1 \hspace{0.2cm}, | ||
| + | \hspace{0.2cm}I_0 = I_2 = 0 | ||
| + | \hspace{0.05cm},</math> | ||
| + | |||
| + | :<math>W_5 = 1, \hspace{0.2cm}W_1 = W_4 = W_7 = 0.5, \hspace{0.2cm} W_0 = W_3 =W_6 =0, \hspace{0.2cm}W_2 = -0.5 | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | Bei einem Vergleich hinsichtlich der maximalen <i>I<sub>i</sub></i>–Werte wären die Quellensymbolfolgen <i>Q</i><sub>5</sub> und <i>Q</i><sub>7</sub> gleichwertig. Bei Berücksichtigung der unterschiedlichen Energien (<i>E</i><sub>5</sub> = 2, <i>E</i><sub>7</sub> = 3) ist dagegen <i>W</i><sub>5</sub> > <i>W</i><sub>7</sub>.<br> | ||
Revision as of 15:31, 27 December 2016
Contents
- 1 Betrachtetes Szenario im Kapitel 3.7
- 2 MAP– und Maximum–Likelihood–Entscheidungsregel (1)
- 3 MAP– und Maximum–Likelihood–Entscheidungsregel (2)
- 4 ML–Entscheidung bei Gaußscher Störung
- 5 Korrelationsempfänger
- 6 Darstellung des Korrelationsempfängers im Baumdiagramm (1)
- 7 Darstellung des Korrelationsempfängers im Baumdiagramm (2)
- 8 Darstellung des Korrelationsempfängers im Baumdiagramm (3)
Betrachtetes Szenario im Kapitel 3.7
Alle bisher beschriebenen Digitalempfänger treffen stets symbolweise Entscheidungen. Werden dagegen mehrere Symbole gleichzeitig entschieden, so können bei der Detektion statistische Bindungen zwischen den Empfangssignalabtastwerten berücksichtigt werden, was eine geringere Fehlerwahrscheinlichkeit zur Folge hat – allerdings auf Kosten einer zusätzlichen Laufzeit.
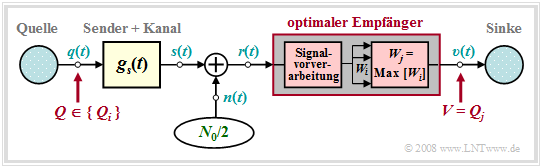
In diesem – teilweise auch im nächsten Kapitel – wird von folgendem Übertragungsmodell ausgegangen:
Gegenüber den letzten Kapiteln 3.5 und 3.6 ergeben sich folgende Unterschiede:
- Q ∈ {Qi} mit i = 0, ... , M–1 bezeichnet eine zeitlich begrenzte Quellensymbolfolge 〈qν〉, deren Symbole vom optimalen Empfänger gemeinsam entschieden werden sollen.
- Beschreibt Q eine Folge von N redundanzfreien Binärsymbolen, so ist M = 2N zu setzen. Dagegen gibt M bei symbolweiser Entscheidung die Stufenzahl der digitalen Quelle an.
- Im obigen Modell werden eventuelle Kanalverzerrungen dem Sender hinzugefügt und sind somit bereits im Grundimpuls gs(t) und im Signal s(t) enthalten. Diese Maßnahme dient lediglich einer einfacheren Darstellung und stellt keine Einschränkung dar.
- Der optimale Empfänger sucht unter Kenntnis des aktuell anliegenden Empfangssignals r(t) aus der Menge {Q0, ... , QM–1} der möglichen Quellensymbolfolgen die am wahrscheinlichsten gesendete Folge {Qj} und gibt diese als Sinkensymbolfolge V aus.
- Vor dem eigentlichen Entscheidungsalgorithmus muss durch eine geeignete Signalvorverarbeitung aus dem Empfangssignal r(t) für jede mögliche Folge Qi ein Zahlenwert Wi abgeleitet werden. Je größer Wi ist, desto größer ist die Rückschlusswahrscheinlichkeit, dass Qi gesendet wurde.
- Die Signalvorverarbeitung muss für die erforderliche Rauschleistungsbegrenzung und – bei starken Kanalverzerrungen – für eine ausreichende Vorentzerrung der entstandenen Impulsinterferenzen sorgen. Außerdem beinhaltet die Vorverarbeitung auch die Abtastung zur Zeitdiskretisierung.
MAP– und Maximum–Likelihood–Entscheidungsregel (1)
Man bezeichnet den (uneingeschränkt) optimalen Empfänger als MAP–Empfänger, wobei „MAP” für „Maximum–a–posteriori” steht.
Die Rückschlusswahrscheinlichkeit Pr(Qi|r(t)) gibt an, mit welcher Wahrscheinlichkeit die Folge Qi gesendet wurde, wenn das Empfangssignal r(t) am Entscheider anliegt. Mit dem Satz von Bayes kann diese Wahrscheinlichkeit wie folgt berechnet werden:
\[{\rm Pr}(Q_i \hspace{0.05cm}|\hspace{0.05cm} r(t)) = \frac{ {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \cdot {\rm Pr}(Q_i)}{{\rm Pr}(r(t))} \hspace{0.05cm}.\]
Die MAP–Entscheidungsregel lässt sich somit wie folgt umformulieren bzw. vereinfachen. Man setze die Sinkensymbolfolge V = Qj, falls für alle i ≠ j gilt:
\[\frac{ {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_j) \cdot {\rm Pr}(Q_j)}{{\rm Pr}(r(t))} > \frac{ {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \cdot {\rm Pr}(Q_i)}{{\rm Pr}(r(t))}\]
\[\Rightarrow \hspace{0.3cm} {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_j) \cdot {\rm Pr}(Q_j)> {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \cdot {\rm Pr}(Q_i) \hspace{0.05cm}.\]
Eine weitere Vereinfachung dieser MAP–Entscheidungsregel führt zum ML–Empfänger, wobei „ML” für „Maximum–Likelihood” steht.
\[{\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_j) > {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \hspace{0.05cm}.\]
Ein Vergleich dieser beiden Definitionen zeigt, dass bei gleichwahrscheinlichen Quellensymbolen der ML– und der MAP–Empfänger gleiche Entscheidungsregeln befolgen und somit vollkommen äquivalent sind. Bei nicht gleichwahrscheinlichen Symbolen ist der ML– dem MAP–Empfänger unterlegen, da er für die Detektion nicht alle zur Verfügung stehenden Informationen nutzt.
MAP– und Maximum–Likelihood–Entscheidungsregel (2)
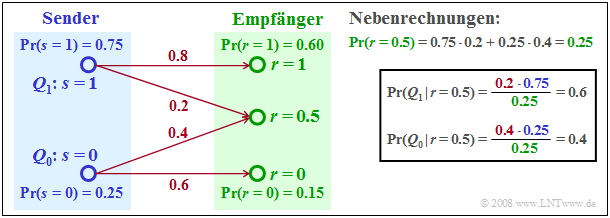
Die Empfangswerte r = 0 und r = 1 werden sowohl vom ML– als auch vom MAP–Entscheider den Senderwerten s = 0 (Q0) bzw. s = 1 (Q1) zugeordnet. Dagegen werden die beiden Entscheider bezüglich des Empfangswertes r = 0.5 zu einem anderen Ergebnis kommen:
- Die Maximum–Likelihood–Entscheidungsregel führt zum Quellensymbol Q0, wegen
- \[{\rm Pr}( r= 0.5\hspace{0.05cm}|\hspace{0.05cm} Q_0) = 0.4 > {\rm Pr}( r= 0.5\hspace{0.05cm}|\hspace{0.05cm} Q_1) = 0.2 \hspace{0.05cm}.\]
- Die MAP–Entscheidung führt dagegen zum Quellensymbol Q1, da entsprechend der Grafik gilt:
- \[{\rm Pr}(Q_1 \hspace{0.05cm}|\hspace{0.05cm} r= 0.5) = 0.6 > {\rm Pr}(Q_0 \hspace{0.05cm}|\hspace{0.05cm} r= 0.5) = 0.4 \hspace{0.05cm}.\]
ML–Entscheidung bei Gaußscher Störung
Wir setzen nun voraus, dass sich das Empfangssignal r(t) additiv aus einem Nutzsignal s(t) und einem Störanteil n(t) zusammensetzt, wobei die Störung als gaußverteilt und weiß angenommen wird (Beispiel: AWGN–Rauschen):
\[r(t) = s(t) + n(t) \hspace{0.05cm}.\]
Eventuelle Kanalverzerrungen werden zur Vereinfachung bereits dem Signal s(t) beaufschlagt.
Die notwendige Rauschleistungsbegrenzung wird durch einen Integrator realisiert; dies entspricht einer Mittelung der Rauschwerte im Zeitbereich. Begrenzt man das Integrationsintervall auf den Bereich t1 bis t2, so kann man für jede Quellensymbolfolge Qi eine Größe Wi ableiten, die ein Maß für die bedingte Wahrscheinlichkeit Pr(r(t)|Qi) darstellt:
\[W_i = \int_{t_1}^{t_2} r(t) \cdot s_i(t) \,{\rm d} t - \frac{1}{2} \cdot \int_{t_1}^{t_2} s_i^2(t) \,{\rm d} t= I_i - \frac{E_i}{2} \hspace{0.05cm}.\]
Diese Entscheidungsgröße Wi kann über die k–dimensioniale Verbundwahrscheinlichkeitsdichte der Störungen (mit k → ∞) und einigen Grenzübergängen hergeleitet werden. Die Gleichung lässt sich wie folgt interpretieren:
- Die Integration dient der Rauschleistungsbegrenzung. Werden vom ML–Detektor N Binärsymbole gleichzeitig entschieden, so ist bei verzerrungsfreiem Kanal t1 = 0 und t2 = NT zu setzen.
- Der erste Term der obigen Entscheidungsgröße Wi ist gleich der über das endliche Zeitintervall NT gebildeten Energie–Kreuzkorrelationsfunktion zwischen r(t) und si(t) an der Stelle τ = 0:
- \[I_i = \varphi_{r, \hspace{0.05cm}s_i} (\tau = 0) = \int_{0}^{NT}r(t) \cdot s_i(t) \,{\rm d} t \hspace{0.05cm}.\]
- Der zweite Term gibt die halbe Energie des betrachteten Nutzsignals si(t) an, die zu subtrahieren ist. Die Energie ist gleich der AKF des Nutzsignals an der Stelle τ = 0:
- \[E_i = \varphi_{s_i} (\tau = 0) = \int_{0}^{NT} s_i^2(t) \,{\rm d} t \hspace{0.05cm}.\]
- Bei verzerrendem Kanal ist die Impulsantwort hK(t) nicht diracförmig, sondern beispielsweise auf den Bereich –TK ≤ t ≤ +TK ausgedehnt. In diesem Fall muss für die beiden Integrationsgrenzen t1 = –TK und t2 = NT + TK eingesetzt werden.
Korrelationsempfänger
Es gibt verschiedene schaltungstechnische Implementierungen des Maximum–Likelihood–Empfängers. Beispielsweise können die erforderlichen Integrale durch lineare Filterung und anschließender Abtastung gewonnen werden. Man bezeichnet diese Realisierungsform als Matched–Filter–Empfänger, da hier die Impulsantworten der M parallelen Filter formgleich mit den Nutzsignalen s0(t), ... , sM–1(t) sind.
Die M Entscheidungsgrößen Ii sind dann gleich den Faltungsprodukten r(t) ∗ si(t) zum Zeitpunkt t = 0. Beispielsweise erlaubt der im Kapitel 1.4 ausführlich beschriebene „optimale Binärempfänger” eine Maximum–Likelihood–Entscheidung mit den ML–Parametern M = 2 und N = 1.
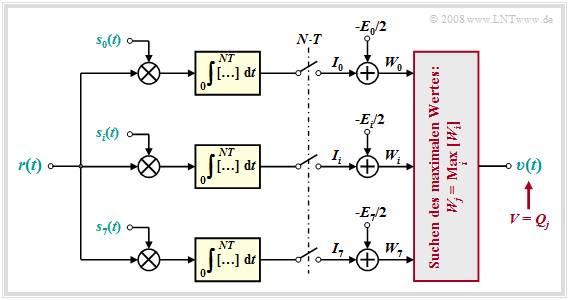
Wir beschränken uns hier auf den sog. Korrelationsempfänger entsprechend obigem Blockschaltbild. Zur Vereinfachung werden N = 3, t1 = 0, t2 = 3T sowie M = 23 = 8 vorausgesetzt. Man erkennt:
- Der Korrelationsempfänger bildet insgesamt M = 8 Kreuzkorrelationsfunktionen zwischen dem Empfangssignal r(t) = sk(t) + n(t) und den möglichen Sendesignalen si(t), i = 0, ... , M–1. Vorausgesetzt ist für diese Beschreibung, dass das Nutzsignal sk(t) gesendet wurde.
- Der Korrelationsempfänger sucht nun den maximalen Wert Wj aller Korrelationswerte und gibt die dazugehörige Folge Qj als Sinkensymbolfolge V aus. Formal lässt sich die ML–Entscheidungsregel wie folgt ausdrücken:
- \[V = Q_j, \hspace{0.2cm}{\rm falls}\hspace{0.2cm} W_j > W_i \hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\rm alle}\hspace{0.2cm} i \ne j \hspace{0.05cm}.\]
- Setzt man weiter voraus, dass alle Sendesignale si(t) die genau gleiche Energie besitzen, so kann man auf die Subtraktion von Ei/2 in allen Zweigen verzichten. In diesem Fall werden folgende Korrelationswerte miteinander verglichen (i = 0, ... , M–1):
- \[I_i = \int_{0}^{NT} s_j(t) \cdot s_i(t) \,{\rm d} t + \int_{0}^{NT} n(t) \cdot s_i(t) \,{\rm d} t \hspace{0.05cm}.\]
- Mit großer Wahrscheinlichkeit ist Ij = Ik größer als alle anderen Vergleichswerte Ii≠k. Ist das Rauschen n(t) allerdings zu groß, so kann auch der ML–Empfänger eine Fehlentscheidung treffen.
Darstellung des Korrelationsempfängers im Baumdiagramm (1)
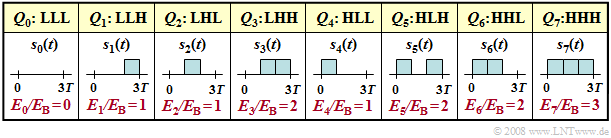
Verdeutlichen wir uns die Funktionsweise des Korrelationsempfängers im Baumdiagramm, wobei die 23 = 8 möglichen Quellensymbolfolgen Qi der Länge N = 3 durch bipolare rechteckförmige Sendesignale si(t) repräsentiert werden. Die möglichen Quellensymbolfolgen Q0 = „LLL”, ... , Q7 = „HHH” und die dazugehörigen Sendesignale s0(t), ... , s7(t) sind nachfolgend aufgeführt.
Wegen den bipolaren Amplitudenkoeffizienten und der Rechteckform sind alle Signalenergien E0, ... , E7 gleich N · EB, wobei EB die Energie eines Einzelimpulses der Dauer T angibt. Deshalb kann auf die Subtraktion des Terms Ei/2 in allen Zweigen verzichtet werden. Eine auf den Korrelationswerten Ii basierende Entscheidung liefert ebenso zuverlässige Ergebnisse wie die Maximierung der korrigierten Werte Wi.
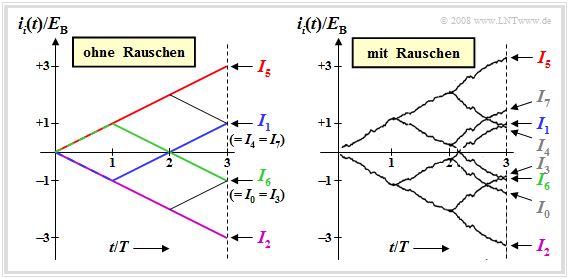
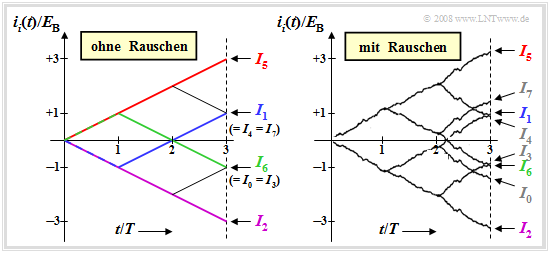
In der linken Grafik sind die fortlaufenden Integralwerte dargestellt, wobei vom tatsächlich gesendeten Signal s5(t) und dem rauschfreien Fall ausgegangen wird:
\[i_i(t) = \int_{0}^{t} r(\tau) \cdot s_i(\tau) \,{\rm d} \tau = \int_{0}^{t} s_5(\tau) \cdot s_i(\tau) \,{\rm d} \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm}I_i = i_i(3T). \]
Das rechte Baumdiagramm berücksichtigt AWGN–Rauschen n(t) mit der Varianz σn2 = 4 · EB/T.
Die Interpretation dieser Grafik folgt auf der nächsten Seite.
Darstellung des Korrelationsempfängers im Baumdiagramm (2)
Es folgt zunächst die Beschreibung des rauschfreien Baumdiagramms (linke Grafik):
- Wegen der Rechteckform der Signale si(t) sind alle Funktionsverläufe ii(t) geradlinig. Die auf 3T normierten Endwerte sind +3, +1, –1 und –3.
- Der maximale Endwert ist I5 = 3EB (roter Kurvenverlauf), da tatsächlich das Signal s5(t) gesendet wurde. Ohne Rauschen trifft der Korrelationsempfänger somit natürlich die richtige Entscheidung.
- Der blaue Kurvenzug i1(t) führt zum Endwert I1 = –EB + EB +EB = EB, da sich s1(t) von s5(t) nur im ersten Bit unterscheidet. Die Vergleichswerte I4 und I7 sind ebenfalls gleich EB.
- Da sich s0(t), s3(t), und s6(t) von s5(t) in zwei Bit unterscheiden, gilt I0 = I3 = I6 = –EB. Die grüne Kurve zeigt i6(t), das zunächst ansteigt (erstes Bit stimmt überein) und dann über zwei Bit abfällt.
- Die violette Kurve führt zum Endwert I2 = –3EB. Das zugehörige Signal s2(t) unterscheidet sich von s5(t) in allen drei Symbolen und es gilt s2(t) = –s5(t).
Im rechten Baumdiagramm sind die Funktionsverläufe aufgrund des Rauschanteils n(t) nicht mehr gerade und es ergeben sich auch etwas andere Endwerte als ohne Rauschen. Im betrachteten Beispiel entscheidet der Korrelationsempfänger mit großer Wahrscheinlichkeit richtig, da die Differenz zwischen I5 und dem nächstgrößeren Wert I7 mit 1.65EB verhältnismäßig groß ist.
Die Fehlerwahrscheinlichkeit ist in dem hier betrachteten Beispiel allerdings nicht besser als die des Matched–Filter–Empfängers mit symbolweiser Entscheidung. Entsprechend Kapitel 1.4 gilt auch hier:
\[p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right) = {1}/{2} \cdot {\rm erfc} \left( \sqrt{{ E_{\rm B}}/{N_0}}\right) \hspace{0.05cm}.\]
Weist das Eingangssignal aber statistische Bindungen auf, so führt die gemeinsame Entscheidung von N Bit zu einer spürbaren Verbesserung, da der ML–Empfänger dies berücksichtigt. Solche Bindungen können entweder durch sendeseitige Codierung bewusst erzeugt werden (siehe Buch „Kanalcodierung”) oder durch (lineare) Kanalverzerrungen ungewollt entstehen.
Bei Vorhandensein solcher Impulsinterferenzen ist die Berechnung der Fehlerwahrscheinlichkeit deutlich schwieriger. Es können jedoch vergleichbare Näherungen wie beim Viterbi–Empfänger angegeben werden, die am Ende von Kapitel 3.8 zu finden sind.
Darstellung des Korrelationsempfängers im Baumdiagramm (3)
Bei unipolarer Signalisierung führt eine auf Ii basierende Entscheidung nicht zum richtigen Ergebnis. Hier muss vielmehr auf die korrigierten Vergleichswerte Wi = Ii – Ei/2 zurückgegriffen werden.
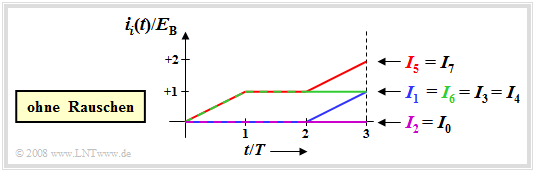
Nachfolgend sehen Sie das Baumdiagramm für den rauschfreien Fall, wobei wie auf der letzten Seite vorausgesetzt ist, dass s5(t) gesendet wurde. Auch die Farben korrespondieren mit der Grafik auf der letzten Seite.
Für dieses Beispiel ergeben sich folgende Vergleichswerte, jeweils normiert auf EB:
\[I_5 = I_7 = 2, \hspace{0.2cm}I_1 = I_3 = I_4= I_6 = 1 \hspace{0.2cm}, \hspace{0.2cm}I_0 = I_2 = 0 \hspace{0.05cm},\]
\[W_5 = 1, \hspace{0.2cm}W_1 = W_4 = W_7 = 0.5, \hspace{0.2cm} W_0 = W_3 =W_6 =0, \hspace{0.2cm}W_2 = -0.5 \hspace{0.05cm}.\]
Bei einem Vergleich hinsichtlich der maximalen Ii–Werte wären die Quellensymbolfolgen Q5 und Q7 gleichwertig. Bei Berücksichtigung der unterschiedlichen Energien (E5 = 2, E7 = 3) ist dagegen W5 > W7.