Difference between revisions of "Aufgaben:Exercise 2.1Z: DSB-AM without/with Carrier"
From LNTwww
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID987__Mod_Z_2_1.png|right|]] |
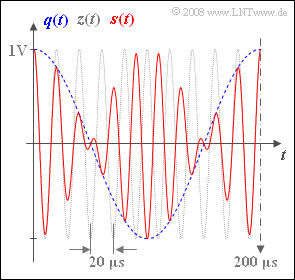
| + | Die Grafik zeigt mit dem roten Kurvenverlauf einen Ausschnitt des Sendesignals$s(t) = q(t) · z(t)$ bei der Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $200 μs$. | ||
| + | Zusätzlich sind das Quellensignal (als blau–gestrichelte Kurve) | ||
| + | $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})$$ | ||
| + | und das Trägersignal (grau–gepunkteter Verlauf) | ||
| + | $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ | ||
| + | in der nebenstehenden Grafik eingetragen. | ||
| + | Ab der Teilaufgabe d) wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_T = 2 V$: | ||
| + | $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [http://en.lntwww.de/Modulationsverfahren/Zweiseitenband-Amplitudenmodulation Kapitel 2.1]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Ermitteln Sie die Phasenwerte von Quellen– und Trägersignal aus der Grafik. |
| + | |type="{}"} | ||
| + | $\phi_N$ = { 0 3% } $\text{Grad}$ | ||
| + | $\phi_T$ = { 0 3% } $\text{Grad}$ | ||
| + | |||
| + | {Wie lauten die Frequenzen von $q(t)$ und $z(t)$? | ||
| + | |type="{}"} | ||
| + | $f_N$ = { 5 3% } $\text{KHz}$ | ||
| + | $f_T$ { 50 3% } $\text{KHz}$ | ||
| + | |||
| + | {Analysieren Sie die Nulldurchgänge von $s(t)$. Welche Aussagen treffen zu? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + Alle Nulldurchgänge von $z(t)$ bleiben in $s(t)$ erhalten. | |
| − | + | + | + Es gibt weitere Nullstellen, verursacht durch $q(t)$. |
| + | - Es gilt $s(t) = a(t) · cos(ω_T · t)$ mit $a(t) = |q(t)|$. | ||
| + | {Bestimmen Sie die Spektralfunktion $S(f)$ über die Faltung. Welche (positiven) Frequenzen $f_1$ und $f_2 > f_1$ sind im Signal enthalten? | ||
| + | |type="{}"} | ||
| + | $f_1$= { 45 3% } $\text{KHz}$ | ||
| + | $f_2$ = { 55 3% } $\text{KHz}$ | ||
| − | { | + | {Es gelte nun $A_T = 2 V$. Wie groß ist der Modulationsgrad? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $m$ = { 0.5 3% } |
| − | |||
| + | {Welche der Aussagen treffen bei der „ZSB–AM mit Träger” und $A_T = 2 V$ zu? | ||
| + | |type="[]"} | ||
| + | + $S(f)$ beinhaltet nun auch Diracfunktionen bei $±f_T$. | ||
| + | - Die Gewichte dieser Diraclinien sind jeweils 2 V. | ||
| + | + $q(t)$ ist in der Hüllkurve von $s(t)$ zu erkennen. | ||
| + | - Durch den zusätzlichen Trägeranteil bleibt die Leistung unverändert. | ||
</quiz> | </quiz> | ||
Revision as of 23:29, 27 December 2016
Die Grafik zeigt mit dem roten Kurvenverlauf einen Ausschnitt des Sendesignals$s(t) = q(t) · z(t)$ bei der Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $200 μs$.
Zusätzlich sind das Quellensignal (als blau–gestrichelte Kurve) $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})$$ und das Trägersignal (grau–gepunkteter Verlauf) $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ in der nebenstehenden Grafik eingetragen.
Ab der Teilaufgabe d) wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_T = 2 V$: $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.1.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.