Difference between revisions of "Digital Signal Transmission/Approximation of the Error Probability"
| Line 86: | Line 86: | ||
Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.<br> | Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.<br> | ||
| − | == == | + | == Gleichwahrscheinliche Binärsymbole – Fehlerwahrscheinlichkeit (2) == |
| + | <br> | ||
| + | [[File:P ID2021 Dig T 4 3 S2 version1.png|Bedingte Dichtefunktionen bei gleichwahrscheinlichen Symbolen|class=fit]]<br> | ||
| + | |||
| + | Kommen wir nun zur Berechnung der Fehlerwahrscheinlichkeit: | ||
| + | *Bei AWGN–Rauschen mit dem Effektivwert (Streuung) <i>σ<sub>n</sub></i> erhält man in diesem Fall, wie bereits in Kapitel 1.2 mit anderer Nomenklatur berechnet wurde: | ||
| + | |||
| + | ::<math>{\rm Pr}({ \cal E} | m_0) \hspace{-0.1cm} = \hspace{-0.1cm} \int_{-\infty}^{G = 0} p_{r \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \rho } |m_0 ) \,{\rm d} \rho = \int_{-\infty}^{- s_0 } p_{{ n} \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \eta } |m_0 ) \,{\rm d} \eta = </math> | ||
| + | :::::<math>\hspace{-0.05cm} = \hspace{-0.1cm}\int_{-\infty}^{- s_0 } p_{{ n} } ({ \eta } ) \,{\rm d} \eta = | ||
| + | \int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Bei der Herleitung der Gleichung wurde berücksichtigt, dass das AWGN–Rauschen <i>η</i> unabhängig vom Signal (<i>m</i><sub>0</sub> oder <i>m</i><sub>1</sub>) ist und eine symmetrische WDF besitzt. Verwendet wurde zudem das komplementäre Gaußsche Fehlerintegral | ||
| + | |||
| + | ::<math>{\rm Q}(x) = \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Entsprechend gilt für <i>m</i> = <i>m</i><sub>1</sub> ⇔ <i>s</i> = <i>s</i><sub>1</sub> = –2 · <i>E</i><sup> 1/2</sup>: | ||
| + | |||
| + | ::<math>{\rm Pr}({ \cal E} | m_1) = \int_{0}^{\infty} p_{{ r} \hspace{0.05cm}|\hspace{0.05cm}m_1 } ({ \rho } |m_1 ) \,{\rm d} \rho = \int_{- s_1 }^{\infty} p_{{ n} } (\boldsymbol{ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {- s_1 }/{\sigma_n} \right ) | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Mit dem Abstand <i>d</i> = <i>s</i><sub>1</sub> – <i>s</i><sub>0</sub> der zwei Signalraumpunkte lassen sich die beiden Ergebnisse zusammenfassen, wobei noch <nobr>Pr(<i>m</i><sub>0</sub>) + Pr(<i>m</i><sub>1</sub>) = 1</nobr> zu berücksichtigen ist: | ||
| + | |||
| + | ::<math>{\rm Pr}({ \cal E} | m_0) = {\rm Pr}({ \cal E} | m_1) = {\rm Q} \left ( {d}/(2{\sigma_n}) \right )</math> | ||
| + | ::<math>\Rightarrow \hspace{0.3cm}{\rm Pr}({ \cal E} ) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr}(m_0) \cdot {\rm Pr}({ \cal E} | m_0) + {\rm Pr}(m_1) \cdot {\rm Pr}({ \cal E} | m_1)=</math> | ||
| + | :::::<math> \hspace{0.2cm}\hspace{-0.1cm} = \hspace{-0.1cm} \left [ {\rm Pr}(m_0) + {\rm Pr}(m_1) \right ] \cdot | ||
| + | {\rm Q} \left ( {d}/(2{\sigma_n}) \right ) = {\rm Q} \left ( {d}/(2{\sigma_n}) \right ) \hspace{0.05cm}.</math> | ||
| + | |||
| + | Diese Gleichung gilt unter der Voraussetzung <i>G</i> = 0 ganz allgemein, also auch für Pr(<i>m</i><sub>0</sub>) ≠ Pr(<i>m</i><sub>1</sub>). Bei nicht gleichwahrscheinlichen Symbolen lässt sich allerdings die Symbolfehlerwahrscheinlichkeit durch eine andere Entscheidergrenze verkleinern.<br> | ||
| + | |||
| + | <b>Hinweis:</b> Die hier genannte Gleichung gilt auch dann, wenn die Signalraumpunkte keine Skalare sind, sondern durch die Vektoren <b><i>s</i></b><sub>0</sub> und <b><i>s</i></b><sub>1</sub> beschrieben werden. Der Abstand <i>d</i> ergibt sich dann als die Norm des Differenzvektors: | ||
| + | |||
| + | :<math>d = || \hspace{0.05cm} \boldsymbol{ s}_1 - \boldsymbol{ s}_0 \hspace{0.05cm} || | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
{{Display}} | {{Display}} | ||
Revision as of 16:10, 28 December 2016
Contents
Optimale Entscheidung bei binärer Übertragung (1)
Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann: r = s + n:
- Der das Übertragungssystem vollständig beschreibende Vektorraum wird von N = 2 zueinander orthogonalen Basisfunktionen φ1(t) und φ2(t) aufgespannt.
- Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor n = (n1, n2).
- Es gibt nur zwei mögliche Sendesignale (M = 2), die durch die beiden Vektoren s0 = (s01, s02) und s1 = (s11, s12) beschrieben werden:
- \[s_0(t) \hspace{-0.1cm} = \hspace{-0.1cm} s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},\]
- \[s_1(t) \hspace{-0.1cm} = \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.\]
- Die beiden Nachrichten m0 ⇔ s0 und m1 ⇔ s1 sind nicht notwendigermaßen gleichwahrscheinlich.
- Aufgabe des Entscheiders ist es nun, für den gegebenen Empfangsvektor r einen Schätzwert nach der MAP–Entscheidungsregel anzugeben. Diese lautet im vorliegenden Fall:
- \[\hat{m} = {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } |m_i ) ] \hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\}\hspace{0.3cm}{\rm mit}\hspace{0.3cm} \boldsymbol{ r } = \boldsymbol{ \rho } = (\rho_1, \rho_2) \hspace{0.05cm}.\]
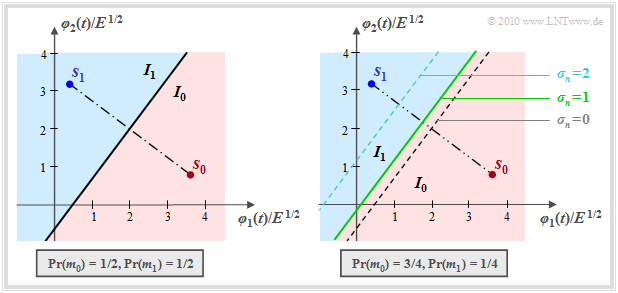
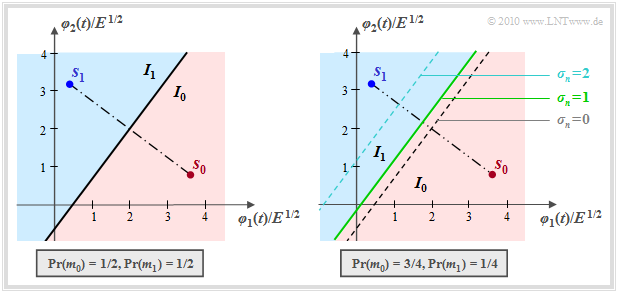
Im hier betrachteten Sonderfall N = 2 und M = 2 partitioniert der Entscheider den zweidimensionalen Raum in die zwei disjunkten Gebiete I0 und I1, wie in der nachfolgenden Grafik verdeutlicht. Liegt der Empfangswert in I0, so wird als Schätzwert m0 ausgegeben, andernfalls m1.
Die Herleitung und Bildbeschreibung folgt auf der nächsten Seite.
Optimale Entscheidung bei binärer Übertragung (2)
Beim AWGN–Kanal und M = 2 lautet somit die Entscheidungsregel: Man entscheide sich immer dann für die Nachricht m0, falls folgende Bedingung erfüllt ist:
\[{\rm Pr}( m_0) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot || \boldsymbol{ \rho } - \boldsymbol{ s }_0 ||^2 \right ] > {\rm Pr}( m_1) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot || \boldsymbol{ \rho } - \boldsymbol{ s }_1 ||^2 \right ] \hspace{0.05cm}.\]
Die Grenzlinie zwischen den beiden Entscheidungsregionen I0 und I1 erhält man, wenn man in obiger Gleichung das Größerzeichen durch das Gleichheitszeichen ersetzt und die Gleichung etwas umformt:
\[|| \boldsymbol{ \rho } - \boldsymbol{ s }_0 ||^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}[{\rm Pr}( m_0)] = || \boldsymbol{ \rho } - \boldsymbol{ s }_1 ||^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}[{\rm Pr}( m_1)] \]
\[\Rightarrow \hspace{0.3cm} || \boldsymbol{ s }_1 ||^2 - || \boldsymbol{ s }_0 ||^2 + 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.\]
Aus dieser Gleichung erkennt man:
- Die Grenzkurve zwischen den Regionen I0 und I1 ist eine Gerade, da die Bestimmungsgleichung linear im Empfangsvektor ρ = (ρ1, ρ2) ist.
- Bei gleichwahrscheinlichen Symbolen verläuft die Grenze genau in der Mitte zwischen s0 und s1 und um 90° verdreht gegenüber der Verbindungslinie zwischen den Sendepunkten (linke Grafik):
- \[|| \boldsymbol{ s }_1 ||^2 - || \boldsymbol{ s }_0 ||^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.\]
- Für Pr(m0) > Pr(m1) ist die Entscheidungsgrenze in Richtung des unwahrscheinlicheren Symbols (s1) verschoben, und zwar um so mehr, je größer die AWGN–Streuung σn ist.
Die grün–durchgezogene Entscheidungsgrenze im rechten Bild sowie die Entscheidungsregionen I0 (rot) und I1 (blau) gelten für die Streuung σn = 1 und die gestrichelten Grenzlinien für σn = 0 bzw. σn = 2.
Gleichwahrscheinliche Binärsymbole – Fehlerwahrscheinlichkeit (1)
Wir gehen weiterhin von einem Binärsystem aus (M = 2), betrachten aber nun den einfachen Fall, dass dieses durch eine einzige Basisfunktion beschrieben werden kann (N = 1). Die Fehlerwahrscheinlichkeit hierfür wurde bereits in Kapitel 1.2 berechnet.
Mit der für Kapitel 4 gewählten Nomenklatur und Darstellungsform ergibt sich folgende Konstellation:
- Der Empfangswert r = s + n – nunmehr ein Skalar – setzt sich aus dem Sendesignal s ∈ {s0, s1} und dem Rauschterm n zusammen. Die Abszisse ρ bezeichnet eine Realisierung von r.
- Die Abszisse ist auf die Bezugsgröße E1/2 normiert, wobei die Normierungsenergie E keine herausgehobene physikalische Bedeutung hat.
- Der Rauschterm n ist gaußverteilt mit dem Mittelwert 0 und der Varianz σn2. Die Wurzel aus der Varianz (σn) wird als Effektivwert oder Streuung bezeichnet.
- Die Entscheidergrenze G unterteilt den gesamten Wertebereich von r in die beiden Teilbereiche I0 (in dem unter anderem s0 liegt) und I1 (mit dem Signalwert s1).
- Ist ρ > G, so liefert der Entscheider den Schätzwert m0, andernfalls m1. Hierbei ist vorausgesetzt, dass die Nachricht mi mit dem Sendesignal si eineindeutig zusammenhängt: mi ⇔ si.
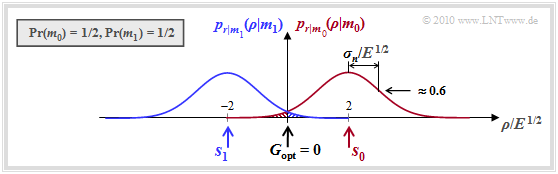
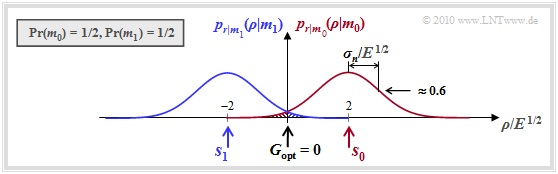
Die Grafik zeigt die bedingten (eindimensionalen) Wahrscheinlichkeitsdichtefunktionen pr|m0 und pr|m1 für den hier betrachteten AWGN–Kanal, wobei gleiche Symbolwahrscheinlichkeiten vorausgesetzt sind: Pr(m0) = Pr(m1) = 0.5. Dementsprechend ist die (optimale) Entscheidergrenze G = 0.
Man erkennt aus dieser Darstellung:
- Ist m = m0 und damit s = s0 = 2 · E 1/2, so kommt es nur dann zu einer Fehlentscheidung, wenn η, die Realisierung der Rauschgröße n, kleiner ist als –2 · E 1/2.
- In diesem Fall ist ρ < 0, wobei ρ eine Realisierung des Empfangswertes r bezeichnet.
Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.
Gleichwahrscheinliche Binärsymbole – Fehlerwahrscheinlichkeit (2)
Kommen wir nun zur Berechnung der Fehlerwahrscheinlichkeit:
- Bei AWGN–Rauschen mit dem Effektivwert (Streuung) σn erhält man in diesem Fall, wie bereits in Kapitel 1.2 mit anderer Nomenklatur berechnet wurde:
- \[{\rm Pr}({ \cal E} | m_0) \hspace{-0.1cm} = \hspace{-0.1cm} \int_{-\infty}^{G = 0} p_{r \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \rho } |m_0 ) \,{\rm d} \rho = \int_{-\infty}^{- s_0 } p_{{ n} \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \eta } |m_0 ) \,{\rm d} \eta = \]
- \[\hspace{-0.05cm} = \hspace{-0.1cm}\int_{-\infty}^{- s_0 } p_{{ n} } ({ \eta } ) \,{\rm d} \eta = \int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) \hspace{0.05cm}.\]
- Bei der Herleitung der Gleichung wurde berücksichtigt, dass das AWGN–Rauschen η unabhängig vom Signal (m0 oder m1) ist und eine symmetrische WDF besitzt. Verwendet wurde zudem das komplementäre Gaußsche Fehlerintegral
- \[{\rm Q}(x) = \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \hspace{0.05cm}.\]
- Entsprechend gilt für m = m1 ⇔ s = s1 = –2 · E 1/2:
- \[{\rm Pr}({ \cal E} | m_1) = \int_{0}^{\infty} p_{{ r} \hspace{0.05cm}|\hspace{0.05cm}m_1 } ({ \rho } |m_1 ) \,{\rm d} \rho = \int_{- s_1 }^{\infty} p_{{ n} } (\boldsymbol{ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {- s_1 }/{\sigma_n} \right ) \hspace{0.05cm}.\]
- Mit dem Abstand d = s1 – s0 der zwei Signalraumpunkte lassen sich die beiden Ergebnisse zusammenfassen, wobei noch <nobr>Pr(m0) + Pr(m1) = 1</nobr> zu berücksichtigen ist:
- \[{\rm Pr}({ \cal E} | m_0) = {\rm Pr}({ \cal E} | m_1) = {\rm Q} \left ( {d}/(2{\sigma_n}) \right )\]
- \[\Rightarrow \hspace{0.3cm}{\rm Pr}({ \cal E} ) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr}(m_0) \cdot {\rm Pr}({ \cal E} | m_0) + {\rm Pr}(m_1) \cdot {\rm Pr}({ \cal E} | m_1)=\]
- \[ \hspace{0.2cm}\hspace{-0.1cm} = \hspace{-0.1cm} \left [ {\rm Pr}(m_0) + {\rm Pr}(m_1) \right ] \cdot {\rm Q} \left ( {d}/(2{\sigma_n}) \right ) = {\rm Q} \left ( {d}/(2{\sigma_n}) \right ) \hspace{0.05cm}.\]
Diese Gleichung gilt unter der Voraussetzung G = 0 ganz allgemein, also auch für Pr(m0) ≠ Pr(m1). Bei nicht gleichwahrscheinlichen Symbolen lässt sich allerdings die Symbolfehlerwahrscheinlichkeit durch eine andere Entscheidergrenze verkleinern.
Hinweis: Die hier genannte Gleichung gilt auch dann, wenn die Signalraumpunkte keine Skalare sind, sondern durch die Vektoren s0 und s1 beschrieben werden. Der Abstand d ergibt sich dann als die Norm des Differenzvektors:
\[d = || \hspace{0.05cm} \boldsymbol{ s}_1 - \boldsymbol{ s}_0 \hspace{0.05cm} || \hspace{0.05cm}.\]