Aufgaben:Exercise 2.7: Is the Modulation Depth Too High?

• Return to book

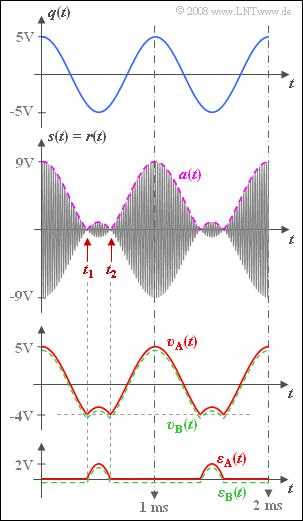
Das cosinusförmige Quellensignal $q(t)$ mit Amplitude $A_N = 5 V$ und Frequenz $f_N = 1 kHz$ wird (ZSB–) amplitudenmoduliert. Für das Empfangssignal gilt bei idealem Kanal: $$r(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$ Es handelt sich also um die „ZSB–AM mit Träger”.

In der Grafik sind neben dem Quellensignal $q(t)$ und dem Empfangssignal $r(t)$ inklusive dessen Hüllkurve $a(t)$ auch das Sinkensignal $υ(t)$ und das Fehlersignal $$ \varepsilon(t) = v(t) - q(t)$$ dargestellt. Das rot gezeichnete Sinkensignal $$v_{\rm A}(t) = a(t) - A_{\rm T}$$ gehört zu einem Hüllkurvendemodulator, bei dem von der Hüllkurve $a(t)$ genau der beim Sender zugeführte Träger ($A_T$) subtrahiert wird. Dieses Signal $υ_A(t)$ besitzt ebenso wie das zugehörige Fehlersignal $ε_A(t)$ einen Gleichanteil. Aufgrund der Periodizität kann es durch die folgende Fourierreihe approximiert werden: $$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),$$ $${\rm mit}\hspace{0.3cm}A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$ $$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$ Wird dagegen der Gleichanteil von a(t) durch einen idealen Hochpass eliminiert, so ergeben sich die gleichsignalfreien Signale $$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),\hspace{0.5cm}\varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$

Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 1.2 und das Kapitel 2.3 dieses Buches sowie auf das Kapitel 2.2 im Buch „Lineare zeitinvariante Systeme”.

Zur Lösung dieser Aufgabe sind folgende unbestimmte Integrale gegeben: $$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$ Die Klirrfaktoren berechnen sich entsprechend $$K_2 = {A_2}/{A_1}, \hspace{0.3cm} K_3 = {A_3}/{A_1}, \hspace{0.1cm} ... \hspace{0.5cm} \Rightarrow \hspace{0.5cm}K = \sqrt{K_2^2 +K_3^2 + ...}\hspace{0.1cm} .$$

Fragebogen

1

Wie groß ist der Modulationsgrad der ZSB–AM?

$m$ =

2

Zu welchen Zeiten $t_1$ und $t_2$ (siehe Grafik) ist die Hüllkurve $a(t)$ erstmalig Null?

$t_1$ = $ms$

$t_2$ = $ms$

3

Berechnen Sie die Klirrfaktoren K2, ..., K6 sowie den Gesamtklirrfaktor K.

$K$= $\text{%}$

4

Berechnen Sie die Leistung $P_{εA} = Ε[ε_A^2(t)] für das rote Fehlersignal ε_A(t).

$P_{εA}$ = $V^2$

5

Berechnen Sie die Leistung $P_{εB} = Ε[ε_B^2(t)]$ für das grüne Fehlersignal $ε_B(t)$.

$P_{εB}$ = $V^2$

6

Berechnen Sie für beide Demodulatoren das jeweilige Sinken–SNR $ρ_υ = P_q/P_ε.

$ρ_{υA}$ =

$ρ_{υB}$ =

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.