Difference between revisions of "Aufgaben:Exercise 2.9: Symmetrical Distortions"
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Modulationsverfahren/Hüllkurvendemodulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |ty…“) |
|||
| Line 2: | Line 2: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1040__Mod_Z_2_8.png|right|]] |
| + | Das aus zwei Anteilen zusammengesetzte Quellensignal | ||
| + | $$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$ | ||
| + | wird amplitudenmoduliert und über einen linear verzerrenden Übertragungskanal übertragen. Die Trägerfrequenz ist $f_T$ und der zugesetzte Gleichanteil $A_T$. Es liegt also eine ZSB–AM mit Träger vor. | ||
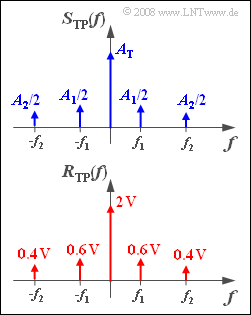
| + | Die obere Grafik zeigt das Spektrum $S_{TP}(f)$ des äquivalenten TP–Signals in schematischer Form. Das bedeutet, dass die Längen der gezeichneten Diraclinien nicht den tatsächlichen Werten von $A_T$, $A_1/2$ und $A_2/2$ entsprechen. | ||
| + | |||
| + | |||
| + | Messtechnisch erfasst wurde die Spektralfunktion $R(f)$ des Empfangssignals. In der unteren Grafik sehen Sie das daraus berechnete äquivalente Tiefpass–Spektrum $R_{TP}(f)$. | ||
| + | |||
| + | Der Kanalfrequenzgang ist durch einige Stützwerte ausreichend genau beschrieben: | ||
| + | $$ H_{\rm K}(f = f_{\rm T}) = 0.5,\hspace{0.3cm}H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,\hspace{0.3cm} H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$ | ||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [http://en.lntwww.de/Modulationsverfahren/H%C3%BCllkurvendemodulation Kapitel 2.3]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 19:45, 1 January 2017
Das aus zwei Anteilen zusammengesetzte Quellensignal $$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$ wird amplitudenmoduliert und über einen linear verzerrenden Übertragungskanal übertragen. Die Trägerfrequenz ist $f_T$ und der zugesetzte Gleichanteil $A_T$. Es liegt also eine ZSB–AM mit Träger vor.
Die obere Grafik zeigt das Spektrum $S_{TP}(f)$ des äquivalenten TP–Signals in schematischer Form. Das bedeutet, dass die Längen der gezeichneten Diraclinien nicht den tatsächlichen Werten von $A_T$, $A_1/2$ und $A_2/2$ entsprechen.
Messtechnisch erfasst wurde die Spektralfunktion $R(f)$ des Empfangssignals. In der unteren Grafik sehen Sie das daraus berechnete äquivalente Tiefpass–Spektrum $R_{TP}(f)$.
Der Kanalfrequenzgang ist durch einige Stützwerte ausreichend genau beschrieben: $$ H_{\rm K}(f = f_{\rm T}) = 0.5,\hspace{0.3cm}H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,\hspace{0.3cm} H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$ Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.3.
Fragebogen
Musterlösung