Difference between revisions of "Aufgaben:Exercise 2.11: Envelope Demodulation of an SSB Signal"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Einseitenbandmodulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |t…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1047__Mod_A_2_10.png|right|]] |
| + | Wir betrachten die Übertragung des Cosinussignals | ||
| + | $$ q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)$$ | ||
| + | gemäß dem Modulationsverfahren „OSB–AM mit Träger”. Beim Empfänger wird das hochfrequente Signal mittels eines Hüllkurvendemodulators in den NF-Bereich zurückgesetzt | ||
| + | |||
| + | Der Kanal wird als ideal vorausgesetzt, so dass $r(t) = s(t)$ gilt. Mit dem Seitenband–zu–Träger–Verhältnis | ||
| + | $$ \mu = \frac{A_{\rm N}}{2 \cdot A_{\rm T}}$$ | ||
| + | kann für das äquivalente TP–Signal auch geschrieben werden: | ||
| + | $$r_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \mu \cdot {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right) \hspace{0.05cm}$$ | ||
| + | Die Hüllkurve – also der Betrag dieses komplexen Signals – kann durch geometrische Überlegungen ermittelt werden. Man erhält abhängig vom Parameter $μ$: | ||
| + | $$a(t ) = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu \cdot \cos(\omega_{\rm N} \cdot t)}\hspace{0.05cm}.$$ | ||
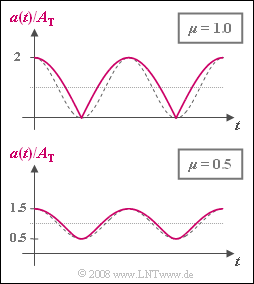
| + | In der Grafik ist die zeitabhängige Hüllkurve a(t) für $μ = 1$ und $μ = 0.5$ dargestellt. Als gestrichelte Vergleichskurven sind jeweils die in der Amplitude angepassten Cosinusschwingungen eingezeichnet, die für eine verzerrungsfreie Demodulation Voraussetzung wären. | ||
| + | |||
| + | Das periodische Signal a(t) kann durch eine Fourierreihe angenähert werden: | ||
| + | $$a(t ) = A_{\rm 0} + A_{\rm 1} \cdot \cos(\omega_{\rm N} \cdot t) + A_{\rm 2} \cdot \cos(2\omega_{\rm N} \cdot t)+ A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t)\hspace{0.05cm}+...$$ | ||
| + | Die Fourierkoeffizienten wurden mit Hilfe eines Simulationsprogrammes ermittelt. Für $μ = 1$ ergaben sich folgende Werte: | ||
| + | $$A_{\rm 0} = 1.273\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.849\,{\rm V},\hspace{0.3cm}A_{\rm 2} = -0.170\,{\rm V},\hspace{0.3cm} A_{\rm 3} = 0.073\,{\rm V},\hspace{0.3cm}A_{\rm 4} = 0.040\,{\rm V} \hspace{0.05cm}.$$ | ||
| + | Entsprechend ergab die Simulation mit $μ = 0.5$: | ||
| + | $$A_{\rm 0} = 1.064\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.484\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.058\,{\rm V} \hspace{0.05cm}.$$ | ||
| + | Die hier nicht angegebenen Werte können bei der Berechnung des Klirrfaktors vernachlässigt werden. Das Sinkensignal $υ(t)$ ergibt sich aus $a(t)$ wie folgt: | ||
| + | $$v(t) = 2 \cdot [a(t ) - A_{\rm 0}] \hspace{0.05cm}.$$ | ||
| + | Der Faktor 2 korrigiert dabei die Amplitudenminderung durch die ESB–AM, während die Subtraktion des Gleichsignalkoeffizienten $A_0$ den Einfluss des Hochpasses innerhalb des Hüllkurvendemodulators berücksichtigt. | ||
| + | |||
| + | Für die Teilaufgaben a) bis c) wird $A_N = 2 V$, $A_T = 1 V$ und somit $μ = 1$ vorausgesetzt, während ab Frage d) der Parameter $μ = 0.5 (A_N = A_T = 1 V)$ festgelegt ist. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf den Theorieteil von [http://en.lntwww.de/Modulationsverfahren/Einseitenbandmodulation Kapitel 2.4]. Vergleichen Sie Ihre Ergebnisse auch mit der Faustformel, die besagt, dass bei der Hüllkurvendemodulation eines ESB–AM–Signals mit dem Seitenband–zu–Träger–Verhältnis $μ$ der Klirrfaktor $K ≈ μ/4$ beträgt. | ||
Revision as of 11:20, 2 January 2017
Wir betrachten die Übertragung des Cosinussignals $$ q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)$$ gemäß dem Modulationsverfahren „OSB–AM mit Träger”. Beim Empfänger wird das hochfrequente Signal mittels eines Hüllkurvendemodulators in den NF-Bereich zurückgesetzt
Der Kanal wird als ideal vorausgesetzt, so dass $r(t) = s(t)$ gilt. Mit dem Seitenband–zu–Träger–Verhältnis $$ \mu = \frac{A_{\rm N}}{2 \cdot A_{\rm T}}$$ kann für das äquivalente TP–Signal auch geschrieben werden: $$r_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \mu \cdot {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right) \hspace{0.05cm}$$ Die Hüllkurve – also der Betrag dieses komplexen Signals – kann durch geometrische Überlegungen ermittelt werden. Man erhält abhängig vom Parameter $μ$: $$a(t ) = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu \cdot \cos(\omega_{\rm N} \cdot t)}\hspace{0.05cm}.$$ In der Grafik ist die zeitabhängige Hüllkurve a(t) für $μ = 1$ und $μ = 0.5$ dargestellt. Als gestrichelte Vergleichskurven sind jeweils die in der Amplitude angepassten Cosinusschwingungen eingezeichnet, die für eine verzerrungsfreie Demodulation Voraussetzung wären.
Das periodische Signal a(t) kann durch eine Fourierreihe angenähert werden: $$a(t ) = A_{\rm 0} + A_{\rm 1} \cdot \cos(\omega_{\rm N} \cdot t) + A_{\rm 2} \cdot \cos(2\omega_{\rm N} \cdot t)+ A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t)\hspace{0.05cm}+...$$ Die Fourierkoeffizienten wurden mit Hilfe eines Simulationsprogrammes ermittelt. Für $μ = 1$ ergaben sich folgende Werte: $$A_{\rm 0} = 1.273\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.849\,{\rm V},\hspace{0.3cm}A_{\rm 2} = -0.170\,{\rm V},\hspace{0.3cm} A_{\rm 3} = 0.073\,{\rm V},\hspace{0.3cm}A_{\rm 4} = 0.040\,{\rm V} \hspace{0.05cm}.$$ Entsprechend ergab die Simulation mit $μ = 0.5$: $$A_{\rm 0} = 1.064\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.484\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.058\,{\rm V} \hspace{0.05cm}.$$ Die hier nicht angegebenen Werte können bei der Berechnung des Klirrfaktors vernachlässigt werden. Das Sinkensignal $υ(t)$ ergibt sich aus $a(t)$ wie folgt: $$v(t) = 2 \cdot [a(t ) - A_{\rm 0}] \hspace{0.05cm}.$$ Der Faktor 2 korrigiert dabei die Amplitudenminderung durch die ESB–AM, während die Subtraktion des Gleichsignalkoeffizienten $A_0$ den Einfluss des Hochpasses innerhalb des Hüllkurvendemodulators berücksichtigt.
Für die Teilaufgaben a) bis c) wird $A_N = 2 V$, $A_T = 1 V$ und somit $μ = 1$ vorausgesetzt, während ab Frage d) der Parameter $μ = 0.5 (A_N = A_T = 1 V)$ festgelegt ist.
Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.4. Vergleichen Sie Ihre Ergebnisse auch mit der Faustformel, die besagt, dass bei der Hüllkurvendemodulation eines ESB–AM–Signals mit dem Seitenband–zu–Träger–Verhältnis $μ$ der Klirrfaktor $K ≈ μ/4$ beträgt.
Fragebogen
Musterlösung