Difference between revisions of "Mobile Communications/Distance Dependent Attenuation and Shading"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Zeitvariante Übertragungskanäle |Vorherige Seite= |Nächste Seite=Wahrscheinlichkeitsdichte des Rayleigh–Fadings }} {{Display}}“) |
|||
| Line 1: | Line 1: | ||
| − | + | {{FirstPage}} | |
{{Header | {{Header | ||
|Untermenü=Zeitvariante Übertragungskanäle | |Untermenü=Zeitvariante Übertragungskanäle | ||
| Line 6: | Line 6: | ||
}} | }} | ||
| + | == Physikalische Beschreibung des Mobilfunkkanals == | ||
| + | <br> | ||
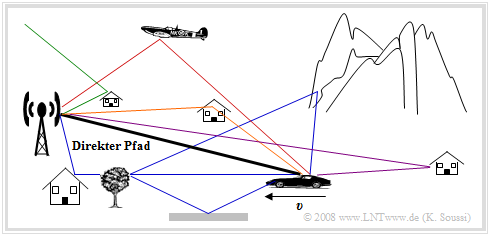
| + | Die Grafik zeigt ein typisches Mobilfunkszenario mit fester Basisstation und einem mobilen Teilnehmer, der sich mit der Geschwindigkeit <i>υ</i> auf die Basisstation zu bewegt. Bei dieser Darstellung erreicht das Funksignal die Mobilstation über einen direkten Pfad. Die Antenne des mobilen Teilnehmers empfängt aber auch noch weitere Signalanteile, die auf Umwegen zum Empfänger gelangen, zum Beispiel aufgrund von Reflexionen an Häusern, einem Gebirge, einem Flugzeug, der Ionosphäre oder dem Erdboden.<br> | ||
| + | [[File:P ID2095 Mob T 1 1 S1 v1.png|Mobilfunkszenario|class=fit]]<br> | ||
| + | Anhand dieses Szenarios lassen sich wichtige Probleme bei der Mobilkommunikation erklären: | ||
| + | *Pfadverlust (englisch: <i>Path Loss</i>): Dieser erfasst die Dämpfung der elektromagnetischen Welle, die in starkem Maße von der Entfernung zwischen Sender und Empfänger abhängt.<br> | ||
| + | *Abschattung (englisch: <i>Shadowing, Long Term Fading</i>): Diese bezeichnet eine langsame Veränderung der Empfangsbedingungen aufgrund der sich ändernden Umgebung, zum Beispiel, wenn man an einem Gebäude vorbeifährt oder wenn man ein Waldstück verlässt.<br> | ||
| + | *Mehrwegeausbreitung (englisch: <i>Multipath Propagation</i>): Gelangt das Signal auf mehreren Wegen mit Laufzeitunterschieden zum Empfänger, so kommt es – je nach Signalfrequenz – zu konstruktiven oder destruktiven Überlagerungen bis hin zu völliger Auslöschung. Für bestimmte Frequenzen ist die Topologie günstig, für andere ungünstig. Deshalb wird dieser Effekt auch als <i>frequenzselektives Fading</i> bezeichnet.<br> | ||
| + | |||
| + | *Zeitvarianz (englisch: <i>Time Variation</i>): Der Effekt entsteht durch die Bewegung de Senders und/oder des Empfängers, da zu jeder Zeit ein anderer Kanal vorliegt. Die Übertragungsqualität sinkt rapide, wenn der direkte Pfad durch ein Hindernis abgeschattet ist. Das Empfangssignal setzt sich dann nur aus den auf Umwegen eintreffenden Teilsignalen zusammen, die aufgrund von Streuungen an Bäumen und Sträuchern sowie eventuell Brechungs– und Beugungserscheinungen gegenüber dem direkten Pfad abgeschwächt sind und sich vektoriell zum Gesamtsignal addieren.<br> | ||
| + | |||
| + | *Dopplereffekt (englisch: <i>Doppler Spread</i>): Je nachdem, ob (und auch in welchem Winkel) sich die Mobilstation auf den Sender zu bewegt oder sich von diesem entfernt, kommt es zu (leichten) Frequenzverschiebungen und damit zu statistischen Bindungen innerhalb des empfangenen Signals, die Impulsinterferenzen bewirken.<br><br> | ||
| + | |||
| + | In Kapitel 1.1 betrachten wir Pfadverlust und Abschattungseffekte genauer. Die Zeitvarianz ist Inhalt von Kapitel 1.2 und 1.4, auch unter Berücksichtigung des Dopplereffektes (Kapitel 1.3). Das Kapitel 2 beschreibt die Mehrwegeausbreitung, die beim Mobilfunk Echos zur Folge hat.<br> | ||
| + | |||
| + | |||
| + | == Freiraumausbreitung == | ||
| + | <br> | ||
| + | Man spricht von Freiraumausbreitung, wenn zwischen Sender und Empfänger (im Abstand <i>d</i>) eine Sichtverbindung besteht wie bei der Satellitenkommunikation oder im Weltraum. Die Radiowellen breiten sich im „leeren Raum” ungehindert kugelförmig um die Sendeantenne aus, werden aber aufgrund des Energieerhaltungssatzes mit zunehmender Entfernung abgeschwächt.<br> | ||
| + | |||
| + | Geometrisch kann man sich das so vorstellen, dass der Radius <i>R</i> der Kugel und damit auch die Kugelfläche immer größer und bei konstanter Gesamtenergie der Energieanteil pro Flächeneinheit proportional zu 1/<i>R</i><sup>2</sup> immer kleiner wird.<br> | ||
| + | |||
| + | Wir gehen von einer unmodulierten Schwingung der Frequenz <i>f</i><sub>S</sub> bzw. der Wellenlänge <i>λ</i> = <i>c</i>/<i>f</i><sub>S</sub> aus, wobei <i>c</i> = 3 · 10<sup>8</sup> m/s die Lichtgeschwindigkeit angibt. Die Signalleistung sei <i>P</i><sub>S</sub>.<br> | ||
| + | |||
| + | Harald Friis hat 1944 eine Gleichung für die Empfangsleistung <i>P</i><sub>E</sub>(<i>d</i>) im Abstand <i>d</i> angegeben, die allerdings nur im Vakuum gültig ist: | ||
| + | |||
| + | :<math>P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} \cdot \lambda^2}{16 \cdot \pi^2 \cdot d^2 \cdot V_{\rm zus}} = | ||
| + | \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm zus}}{K_{\rm FR}(d)} \hspace{0.05cm}.</math> | ||
| + | |||
| + | <i>G</i><sub>S</sub> bzw. <i>G</i><sub>E</sub> bezeichnen die Antennengewinne von Sender und Empfänger. <i>V</i><sub>zus</sub> > 1 fasst alle Verluste zusammen, die unabhängig von der Wellenausbreitung sind, z.B. die Verluste durch die Antennen–Kabelzuführungen. Die Freiraumdämpfung <i>K</i><sub>FR</sub>(<i>d</i>) hängt von der Distanz <i>d</i> ab: | ||
| + | |||
| + | :<math>K_{\rm FR}(d) = K_{\rm FR}(d_0) \cdot (d/d_0)^2 \hspace{0.2cm}{\rm mit} \hspace{0.2cm} | ||
| + | K_{\rm FR}(d_0) = \left [{4 \cdot \pi \cdot d_0}/{\lambda} \right ]^2 \hspace{0.05cm}.</math> | ||
| + | |||
| + | Meist wird die Freiraumdämpfung logarithmisch mit der Pseudoeinheit „dB” angegeben. Dann gilt für den Leistungsverlust durch die Freiraumdämpfung („<i>V</i>” steht für „Verlust” in dB): | ||
| + | |||
| + | :<math>V_{\rm FR}(d) \hspace{-0.1cm} = \hspace{-0.1cm} 10 \cdot {\rm lg} \hspace{0.1cm} K_{\rm FR}(d) = V_{\rm 0} + 20\,\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},</math> | ||
| + | :<math>V_{\rm 0} \hspace{-0.1cm} = \hspace{-0.1cm} V_{\rm FR}(d_0) = 20\,\,{\rm dB} \cdot {\rm lg} \hspace{0.2cm} ({4 \pi d_0}/{\lambda}) \hspace{0.05cm}.</math> | ||
| + | |||
| + | Zu diesen Gleichungen ist anzumerken: | ||
| + | *Sie gilt nur im Fernfeld der Antenne (<i>d</i> > <i>d</i><sub>F</sub>). <i>d</i><sub>F</sub> = 2 <i>D</i><sup>2</sup>/<i>λ</i> ist die Fraunhofer–Distanz. Für <i>D</i> ist hierbei die größte physikalische Abmessung der Sendeantenne einzusetzen.<br> | ||
| + | |||
| + | *Die obige Formel gilt nicht für <i>d</i> → 0. Hierfür ergäbe sich der Grenzwert <i>K</i><sub>FR</sub> → 0, und es ergäbe sich unabhängig von <i>P</i><sub>S</sub> stets eine unendliche Empfangsleistung <i>P</i><sub>E</sub>(<i>d</i> → 0).<br> | ||
| + | |||
| + | *Die Freiraumdämpfung <i>K</i><sub>FR</sub>(<i>d</i>) nimmt mit zunehmender Entfernung <i>d</i> quadratisch zu und ebenfalls quadratisch mit zunehmender Signalfrequenz <i>f</i><sub>S</sub>, das heißt, mit kleiner werdender Wellenlänge <i>λ</i>.<br> | ||
| + | |||
| + | *Beispielsweise gilt beim GSM/E–Netz (<i>f</i><sub>S</sub> = 1.8 GHz ⇒ <i>λ</i> ≈ 17 cm): <i>K</i><sub>FR</sub>(<i>d</i> = 1 km) = 1.6 · 10<sup>9</sup>. Beim Empfänger im Abstand von 1 km kommt also nicht mal ein Milliardstel der Sendeleistung an.<br><br> | ||
| + | |||
| + | In der Aufgabe Z1.1 soll die obige Friis–Gleichung numerisch ausgewertet und interpretiert werden. Oft setzt man die Freiraumdämpfung in Bezug zu einer geeignet zu definierenden Normierungsdistanz <i>d</i><sub>0</sub>, wobei man häufig <i>d</i><sub>0</sub> = 1 m verwendet.<br> | ||
{{Display}} | {{Display}} | ||
Revision as of 16:24, 4 January 2017
Physikalische Beschreibung des Mobilfunkkanals
Die Grafik zeigt ein typisches Mobilfunkszenario mit fester Basisstation und einem mobilen Teilnehmer, der sich mit der Geschwindigkeit υ auf die Basisstation zu bewegt. Bei dieser Darstellung erreicht das Funksignal die Mobilstation über einen direkten Pfad. Die Antenne des mobilen Teilnehmers empfängt aber auch noch weitere Signalanteile, die auf Umwegen zum Empfänger gelangen, zum Beispiel aufgrund von Reflexionen an Häusern, einem Gebirge, einem Flugzeug, der Ionosphäre oder dem Erdboden.
Anhand dieses Szenarios lassen sich wichtige Probleme bei der Mobilkommunikation erklären:
- Pfadverlust (englisch: Path Loss): Dieser erfasst die Dämpfung der elektromagnetischen Welle, die in starkem Maße von der Entfernung zwischen Sender und Empfänger abhängt.
- Abschattung (englisch: Shadowing, Long Term Fading): Diese bezeichnet eine langsame Veränderung der Empfangsbedingungen aufgrund der sich ändernden Umgebung, zum Beispiel, wenn man an einem Gebäude vorbeifährt oder wenn man ein Waldstück verlässt.
- Mehrwegeausbreitung (englisch: Multipath Propagation): Gelangt das Signal auf mehreren Wegen mit Laufzeitunterschieden zum Empfänger, so kommt es – je nach Signalfrequenz – zu konstruktiven oder destruktiven Überlagerungen bis hin zu völliger Auslöschung. Für bestimmte Frequenzen ist die Topologie günstig, für andere ungünstig. Deshalb wird dieser Effekt auch als frequenzselektives Fading bezeichnet.
- Zeitvarianz (englisch: Time Variation): Der Effekt entsteht durch die Bewegung de Senders und/oder des Empfängers, da zu jeder Zeit ein anderer Kanal vorliegt. Die Übertragungsqualität sinkt rapide, wenn der direkte Pfad durch ein Hindernis abgeschattet ist. Das Empfangssignal setzt sich dann nur aus den auf Umwegen eintreffenden Teilsignalen zusammen, die aufgrund von Streuungen an Bäumen und Sträuchern sowie eventuell Brechungs– und Beugungserscheinungen gegenüber dem direkten Pfad abgeschwächt sind und sich vektoriell zum Gesamtsignal addieren.
- Dopplereffekt (englisch: Doppler Spread): Je nachdem, ob (und auch in welchem Winkel) sich die Mobilstation auf den Sender zu bewegt oder sich von diesem entfernt, kommt es zu (leichten) Frequenzverschiebungen und damit zu statistischen Bindungen innerhalb des empfangenen Signals, die Impulsinterferenzen bewirken.
In Kapitel 1.1 betrachten wir Pfadverlust und Abschattungseffekte genauer. Die Zeitvarianz ist Inhalt von Kapitel 1.2 und 1.4, auch unter Berücksichtigung des Dopplereffektes (Kapitel 1.3). Das Kapitel 2 beschreibt die Mehrwegeausbreitung, die beim Mobilfunk Echos zur Folge hat.
Freiraumausbreitung
Man spricht von Freiraumausbreitung, wenn zwischen Sender und Empfänger (im Abstand d) eine Sichtverbindung besteht wie bei der Satellitenkommunikation oder im Weltraum. Die Radiowellen breiten sich im „leeren Raum” ungehindert kugelförmig um die Sendeantenne aus, werden aber aufgrund des Energieerhaltungssatzes mit zunehmender Entfernung abgeschwächt.
Geometrisch kann man sich das so vorstellen, dass der Radius R der Kugel und damit auch die Kugelfläche immer größer und bei konstanter Gesamtenergie der Energieanteil pro Flächeneinheit proportional zu 1/R2 immer kleiner wird.
Wir gehen von einer unmodulierten Schwingung der Frequenz fS bzw. der Wellenlänge λ = c/fS aus, wobei c = 3 · 108 m/s die Lichtgeschwindigkeit angibt. Die Signalleistung sei PS.
Harald Friis hat 1944 eine Gleichung für die Empfangsleistung PE(d) im Abstand d angegeben, die allerdings nur im Vakuum gültig ist:
\[P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} \cdot \lambda^2}{16 \cdot \pi^2 \cdot d^2 \cdot V_{\rm zus}} = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm zus}}{K_{\rm FR}(d)} \hspace{0.05cm}.\]
GS bzw. GE bezeichnen die Antennengewinne von Sender und Empfänger. Vzus > 1 fasst alle Verluste zusammen, die unabhängig von der Wellenausbreitung sind, z.B. die Verluste durch die Antennen–Kabelzuführungen. Die Freiraumdämpfung KFR(d) hängt von der Distanz d ab:
\[K_{\rm FR}(d) = K_{\rm FR}(d_0) \cdot (d/d_0)^2 \hspace{0.2cm}{\rm mit} \hspace{0.2cm} K_{\rm FR}(d_0) = \left [{4 \cdot \pi \cdot d_0}/{\lambda} \right ]^2 \hspace{0.05cm}.\]
Meist wird die Freiraumdämpfung logarithmisch mit der Pseudoeinheit „dB” angegeben. Dann gilt für den Leistungsverlust durch die Freiraumdämpfung („V” steht für „Verlust” in dB):
\[V_{\rm FR}(d) \hspace{-0.1cm} = \hspace{-0.1cm} 10 \cdot {\rm lg} \hspace{0.1cm} K_{\rm FR}(d) = V_{\rm 0} + 20\,\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},\] \[V_{\rm 0} \hspace{-0.1cm} = \hspace{-0.1cm} V_{\rm FR}(d_0) = 20\,\,{\rm dB} \cdot {\rm lg} \hspace{0.2cm} ({4 \pi d_0}/{\lambda}) \hspace{0.05cm}.\]
Zu diesen Gleichungen ist anzumerken:
- Sie gilt nur im Fernfeld der Antenne (d > dF). dF = 2 D2/λ ist die Fraunhofer–Distanz. Für D ist hierbei die größte physikalische Abmessung der Sendeantenne einzusetzen.
- Die obige Formel gilt nicht für d → 0. Hierfür ergäbe sich der Grenzwert KFR → 0, und es ergäbe sich unabhängig von PS stets eine unendliche Empfangsleistung PE(d → 0).
- Die Freiraumdämpfung KFR(d) nimmt mit zunehmender Entfernung d quadratisch zu und ebenfalls quadratisch mit zunehmender Signalfrequenz fS, das heißt, mit kleiner werdender Wellenlänge λ.
- Beispielsweise gilt beim GSM/E–Netz (fS = 1.8 GHz ⇒ λ ≈ 17 cm): KFR(d = 1 km) = 1.6 · 109. Beim Empfänger im Abstand von 1 km kommt also nicht mal ein Milliardstel der Sendeleistung an.
In der Aufgabe Z1.1 soll die obige Friis–Gleichung numerisch ausgewertet und interpretiert werden. Oft setzt man die Freiraumdämpfung in Bezug zu einer geeignet zu definierenden Normierungsdistanz d0, wobei man häufig d0 = 1 m verwendet.