Difference between revisions of "Aufgaben:Exercise 5.8: Equalization in Matrix Vector Notation"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1663__A_5_8.png|right|]] |
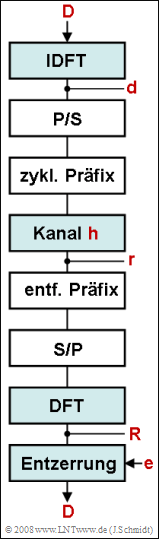
| + | Wir betrachten die in der Grafik hinterlegten Blöcke eines OFDM–Systems, wobei wir von einem System mit N = 4 Trägern und einem Kanal mit L = 2 Echos ausgehen. Es wird nur ein einziger Rahmen betrachtet und für den Sendevektor (im Zeitbereich) gelte: | ||
| + | $${\rm\bf{d}} = (d_0, d_1,d_2,d_3 ) = (+1, -1, +1, -1 ).$$ | ||
| + | Die Kanalimpulsantwort sei beschrieben durch | ||
| + | $${\rm\bf{h}} = (h_0, h_1,h_2 ) = (0, 0.6, 0.4 ).$$ | ||
| + | Zur Repräsentation des zyklischen Präfixes verwenden wir in dieser Aufgabe statt des erweiterten Sendevektors mit der zugehörigen Übertragungsmatrix $H_{ext}$ die zyklische Übertragungsmatrix | ||
| + | $${\rm\bf{H}}_{\rm{C}} = \left( {\begin{array}{*{20}c} {h_0 } & {h_1 } & {h_2 } & {} \\ {} & {h_0 } & {h_1 } & {h_2 } \\ \hline {h_2 } & {} & {h_0 } & {h_1 } \\ {h_1 } & {h_2 } & {} & {h_0 } \\ \end{array}} \right).$$ | ||
| + | Für die Spektralkoeffizienten am Empfänger gelte nach der Diskreten Fouriertransformation (DFT): | ||
| + | $${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) ,$$ | ||
| + | wobei die Diagonalelemente wie folgt zu berechnen sind: | ||
| + | $$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm} {\mu }/{4}} } .$$ | ||
| + | Die Entzerrung am Empfänger erfolgt durch Multiplikation im Frequenzbereich mit den Koeffizienten | ||
| + | $$ e_\mu = {1}/{H_\mu }.$$ | ||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://en.lntwww.de/Modulationsverfahren/Realisierung_von_OFDM-Systemen Kapitel 5.6] dieses Buches sowie auf das [http://en.lntwww.de/Signaldarstellung/Diskrete_Fouriertransformation_(DFT) Kapitel 5.2] im Buch „Signaldarstellung”. Für die Diskrete Fouriertransformation (DFT) gilt in Matrix–Vektor–Notation: | ||
| + | $${\rm\bf{F}} = \left( {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 1 & {} & {} & {} \\ \vdots & {} & {{\rm{e}}^{ - {\rm{j2\pi }}{\kern 1pt} \nu {\kern 1pt} \mu /N} } & {} \\ 1 & {} & {} & {} \\ \end{array}} \right), \qquad {\rm{DFT\; mit}} \; {1}/{N} \cdot {\rm\bf{F}}; \qquad {\rm{IDFT \; mit}} \; {\rm\bf{F}}^*.$$ | ||
| + | |||
| Line 9: | Line 24: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Berechnen Sie die diskreten Empfangsswerte $r = (r_0, r_1, r_2, r_3)$ im Zeitbereich. Geben Sie zur Kontrolle $r_0$ und $r_1$ ein: |
| − | |type=" | + | |type="{}"} |
| − | - | + | Re{$r_0$} = { -0.2 3% } |
| − | + | Im{$r_0$} = { 0 3% } | |
| + | Re{$r_1$} = { 0.2 3% } | ||
| + | Im{$r_1$} = { 0 3% } | ||
| + | {Wie lauten die diskreten Spektralbereichskoeffizienten <b>D</b> = (<i>D</i><sub>0</sub>, <i>D</i><sub>1</sub>, <i>D</i><sub>2</sub>, <i>D</i><sub>3</sub>) am Sender? Geben Sie zur Kontrolle <i>D</i><sub>2</sub> und <i>D</i><sub>3</sub> ein: | ||
| + | |type="{}"} | ||
| + | Re{$D_2$}= { 1 3% } | ||
| + | Im{$D_2$} = { 0 3% } | ||
| + | Re{$D_3$}= { 0 3% } | ||
| + | Im{$D_3$} = { 0 3% } | ||
| − | { | + | {Berechnen Sie die diskreten Spektralkoeffizienten <b>R</b> = (<i>R</i><sub>0</sub>, <i>R</i><sub>1</sub>, <i>R</i><sub>2</sub>, <i>R</i><sub>3</sub>) nach dem Kanal. Geben Sie zur Kontrolle <i>R</i><sub>2</sub> und <i>R</i><sub>3</sub> ein: |
|type="{}"} | |type="{}"} | ||
| − | $ | + | Re{$R_2$} = { -0.2 3% } |
| − | + | Im{$R_2$} = { 0 3% } | |
| + | Re{$R_3$} = { 0 3% } | ||
| + | Im{$R_3$} = { 0 3% } | ||
| + | { Bestimmen Sie die diskreten Entzerrerkoeffizienten <b>e</b> = (<i>e</i><sub>0</sub>, <i>e</i><sub>1</sub>, <i>e</i><sub>2</sub>, <i>e</i><sub>3</sub>): | ||
| + | |type="{}"} | ||
| + | Re{$e_0$} = { 1 3% } | ||
| + | Im{$e_0$} = { 0 3% } | ||
| + | Re{$e_1$} = { -0.77 3% } | ||
| + | Im{$e_1$} = { 1.15 3% } | ||
| + | Re{$e_2$} = { -5 3% } | ||
| + | Im{$e_2$} = { 0 3% } | ||
| + | Re{$e_3$} = { -0.77 3% } | ||
| + | Im{$e_3$} = { -1.15 3% } | ||
| + | {Wie bezeichnet man den verwendeten Entzerrungsansatz? | ||
| + | |type="[]"} | ||
| + | + als „Zero Forcing”–Ansatz, | ||
| + | - als „Matched Filter”–Ansatz, | ||
| + | - als „Minimum Mean Square Error (MMSE)”–Ansatz. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Die diskreten Zeitbereichswerte am Empfänger berechnen sich mit der zyklischen Übertragungsmatrix $H_C$ wie folgt: |
| − | '''2.''' | + | $${\rm\bf{r}} = {\rm\bf{d}} \cdot {\rm\bf{H_C}} = \left( {+1 ,-1 ,+1 ,-1 } \right) \cdot \left( {\begin{array}{*{20}c} {0 } & {0.6 } & {0.4 } & {} \\ {} & {0 } & {0.6 } & {0.4 } \\ \hline {0.4 } & {} & {0 } & {0.6 } \\ {0.6 } & {0.4 } & {} & {0 } \\ \end{array}} \right)$$ |
| − | '''3.''' | + | $$\Rightarrow \hspace{0.3cm}{\rm\bf{r}} = \left( {r_0 ,r_1 ,r_2 ,r_3 } \right) = \left( {-0.2, +0.2,-0.2, +0.2} \right) .$$ |
| − | '''4.''' | + | Damit sind alle Empfangswerte <i>r</i><sub>0</sub> <u>= –0.2,</u> <i>r</i><sub>1</sub> <u>= +0.2</u>, <i>r</i><sub>2</sub> = <u>–0.2</u> und <u><i>r</i><sub>3</sub> = +0.2</u> rein reell. |
| − | + | ||
| − | + | '''2.''' Die Spektralkoeffizienten <b>D</b> ergeben sich direkt aus der Diskreten Fouriertransformation (DFT) der Zeitbereichskoeffizienten <b>d</b> = (+1, –1, +1, –1). Diese Zeitbereichsfolge entspricht einer diskreten Cosinusfunktion mit der doppelten Grundfrequnz (2 · <i>f</i><sub>0</sub>) und der Amplitude 1. Daraus folgt: | |
| − | ''' | + | $${\rm\bf{D}} = \left( {D_0 ,D_1 ,D_2 ,D_3 } \right) \hspace{0.15cm} \underline{=\left( {0, 0,1, 0} \right)} .$$ |
| + | |||
| + | '''3.''' Der Vektor <b>R</b> der Spektralkoeffizienten nach dem Kanal könnte analog zur Teilaufgabe b) durch die DFT des Vektors <b>r</b> berechnet werden. Ein alternativer Lösungsweg lautet: | ||
| + | $${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} | ||
| + | {H_0 } & {} & {} & {} \\ | ||
| + | {} & {H_1 } & {} & {} \\ | ||
| + | {} & {} & {H_2 } & {} \\ | ||
| + | {} & {} & {} & {H_3 } \\ | ||
| + | \end{array}} \right) .$$ | ||
| + | Für die Diagonalelemente erhält man: | ||
| + | $$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - | ||
| + | {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} | ||
| + | \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot | ||
| + | \hspace{0.04cm}{\mu }/{4}} }$$ | ||
| + | $$\Rightarrow \hspace{0.3cm} H_0 = 1,\hspace{0.1cm}H_1 = -0.4 - {\rm{j}} \cdot | ||
| + | 0.6,\hspace{0.1cm}H_2 = -0.2,\hspace{0.1cm}H_3 = -0.4 + {\rm{j}} | ||
| + | \cdot 0.6 $$ | ||
| + | $$\Rightarrow \hspace{0.3cm}{\rm\bf{R}} = \left( {R_0 ,R_1 ,R_2 ,R_3 | ||
| + | } \right) \hspace{0.15cm} \underline{= \left( {\hspace{0.15cm}0,\hspace{0.15cm}0,-0.2, \hspace{0.15cm}0} \right)} .$$ | ||
| + | |||
| + | '''4.''' Die Entzerrerkoeffizienten ergeben sich zu <i>e<sub>μ</sub></i> = 1/<i>H<sub>μ</sub></i>. Mit dem Ergebnis zu Teilaufgabe c) sind die Koeffizienten <i>e</i><sub>0</sub> <u>= 1</u> und <i>e</i><sub>2</sub> <u>= –5</u> reell, während für <i>μ</i> = 1, <i>μ</i> = 3 gilt: | ||
| + | $$e_1 = \frac {1}{-0.4 - {\rm{j}} \cdot 0.6}$$ | ||
| + | $$\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_1] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_1] = \frac {0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx 1.15},$$ | ||
| + | $$e_3 = \frac {1}{-0.4 + {\rm{j}} \cdot 0.6}$$ | ||
| + | $$\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_3] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_3] = \frac {-0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx -1.15}.$$ | ||
| + | '''5.''' Die unter d) berechnete Entzerrung folgt dem <u>„Zero Forcing”–Ansatz</u>. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 15:11, 8 January 2017
Wir betrachten die in der Grafik hinterlegten Blöcke eines OFDM–Systems, wobei wir von einem System mit N = 4 Trägern und einem Kanal mit L = 2 Echos ausgehen. Es wird nur ein einziger Rahmen betrachtet und für den Sendevektor (im Zeitbereich) gelte: $${\rm\bf{d}} = (d_0, d_1,d_2,d_3 ) = (+1, -1, +1, -1 ).$$ Die Kanalimpulsantwort sei beschrieben durch $${\rm\bf{h}} = (h_0, h_1,h_2 ) = (0, 0.6, 0.4 ).$$ Zur Repräsentation des zyklischen Präfixes verwenden wir in dieser Aufgabe statt des erweiterten Sendevektors mit der zugehörigen Übertragungsmatrix $H_{ext}$ die zyklische Übertragungsmatrix $${\rm\bf{H}}_{\rm{C}} = \left( {\begin{array}{*{20}c} {h_0 } & {h_1 } & {h_2 } & {} \\ {} & {h_0 } & {h_1 } & {h_2 } \\ \hline {h_2 } & {} & {h_0 } & {h_1 } \\ {h_1 } & {h_2 } & {} & {h_0 } \\ \end{array}} \right).$$ Für die Spektralkoeffizienten am Empfänger gelte nach der Diskreten Fouriertransformation (DFT): $${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) ,$$ wobei die Diagonalelemente wie folgt zu berechnen sind: $$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm} {\mu }/{4}} } .$$ Die Entzerrung am Empfänger erfolgt durch Multiplikation im Frequenzbereich mit den Koeffizienten $$ e_\mu = {1}/{H_\mu }.$$ Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.6 dieses Buches sowie auf das Kapitel 5.2 im Buch „Signaldarstellung”. Für die Diskrete Fouriertransformation (DFT) gilt in Matrix–Vektor–Notation: $${\rm\bf{F}} = \left( {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 1 & {} & {} & {} \\ \vdots & {} & {{\rm{e}}^{ - {\rm{j2\pi }}{\kern 1pt} \nu {\kern 1pt} \mu /N} } & {} \\ 1 & {} & {} & {} \\ \end{array}} \right), \qquad {\rm{DFT\; mit}} \; {1}/{N} \cdot {\rm\bf{F}}; \qquad {\rm{IDFT \; mit}} \; {\rm\bf{F}}^*.$$
Fragebogen
Musterlösung
2. Die Spektralkoeffizienten D ergeben sich direkt aus der Diskreten Fouriertransformation (DFT) der Zeitbereichskoeffizienten d = (+1, –1, +1, –1). Diese Zeitbereichsfolge entspricht einer diskreten Cosinusfunktion mit der doppelten Grundfrequnz (2 · f0) und der Amplitude 1. Daraus folgt: $${\rm\bf{D}} = \left( {D_0 ,D_1 ,D_2 ,D_3 } \right) \hspace{0.15cm} \underline{=\left( {0, 0,1, 0} \right)} .$$
3. Der Vektor R der Spektralkoeffizienten nach dem Kanal könnte analog zur Teilaufgabe b) durch die DFT des Vektors r berechnet werden. Ein alternativer Lösungsweg lautet: $${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) .$$ Für die Diagonalelemente erhält man: $$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm}{\mu }/{4}} }$$ $$\Rightarrow \hspace{0.3cm} H_0 = 1,\hspace{0.1cm}H_1 = -0.4 - {\rm{j}} \cdot 0.6,\hspace{0.1cm}H_2 = -0.2,\hspace{0.1cm}H_3 = -0.4 + {\rm{j}} \cdot 0.6 $$ $$\Rightarrow \hspace{0.3cm}{\rm\bf{R}} = \left( {R_0 ,R_1 ,R_2 ,R_3 } \right) \hspace{0.15cm} \underline{= \left( {\hspace{0.15cm}0,\hspace{0.15cm}0,-0.2, \hspace{0.15cm}0} \right)} .$$
4. Die Entzerrerkoeffizienten ergeben sich zu eμ = 1/Hμ. Mit dem Ergebnis zu Teilaufgabe c) sind die Koeffizienten e0 = 1 und e2 = –5 reell, während für μ = 1, μ = 3 gilt: $$e_1 = \frac {1}{-0.4 - {\rm{j}} \cdot 0.6}$$ $$\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_1] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_1] = \frac {0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx 1.15},$$ $$e_3 = \frac {1}{-0.4 + {\rm{j}} \cdot 0.6}$$ $$\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_3] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_3] = \frac {-0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx -1.15}.$$ 5. Die unter d) berechnete Entzerrung folgt dem „Zero Forcing”–Ansatz.