(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Reed–Solomon–Codes und deren Decodierung |Vorherige Seite=Einige Grundlagen der Algebra |Nächste Seite=Definition und Eigenschaften…“) |
|||
| Line 355: | Line 355: | ||
lassen sich faktorisieren und ergeben keinen Erweiterungskörper. Man nennt die Polynome <i>p</i><sub>2</sub>(<i>x</i>), <i>p</i><sub>3</sub>(<i>x</i>) und <i>p</i><sub>4</sub>(<i>x</i>) <span style="font-weight: bold;">reduzibel</span>.<br> | lassen sich faktorisieren und ergeben keinen Erweiterungskörper. Man nennt die Polynome <i>p</i><sub>2</sub>(<i>x</i>), <i>p</i><sub>3</sub>(<i>x</i>) und <i>p</i><sub>4</sub>(<i>x</i>) <span style="font-weight: bold;">reduzibel</span>.<br> | ||
| − | <b>Anmerkung:</b> Die Umbenennung der Funktionsvariablen <i>α</i> in <i>x</i> hat nur formale Bedeutung im Hinblick auf die folgenden Seiten. | + | <b>Anmerkung:</b> Die Umbenennung der Funktionsvariablen <i>α</i> in <i>x</i> hat nur formale Bedeutung im Hinblick auf die folgenden Seiten.<br> |
| + | == GF(2<sup>2</sup>) – Beispiel eines Erweiterungskörpers (3) == | ||
| + | <br> | ||
| + | Wir betrachten weiterhin den Körper GF(2<sup>2</sup>) = {0, 1, <i>α</i>, 1+<i>α</i>} entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung <b> <i>p</i>(<i>α</i>) = <i>α</i><sup>2</sup> + <i>α</i> + 1 = 0</b> (irreduzibles Ploynom): | ||
| + | <html><style type="text/css">.paddingSpace td {padding:0 15px 0 15px;}</style></html> | ||
| + | <table class="paddingSpace"> | ||
| + | <td> | ||
| + | {| class="wikitable" style="text-align: center; width: 50px; height: 50px;" | ||
| + | |- | ||
| + | ! + | ||
| + | ! 0 | ||
| + | ! 1 | ||
| + | ! α | ||
| + | ! 1+α | ||
| + | |- | ||
| + | ! 0 | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | α | ||
| + | || 1+α | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 1 | ||
| + | | 0 | ||
| + | | 1+α | ||
| + | || α | ||
| + | |- | ||
| + | ! α | ||
| + | | α | ||
| + | | 1+α | ||
| + | | 0 | ||
| + | || 1 | ||
| + | |- | ||
| + | ! 1+α | ||
| + | | 1+α | ||
| + | | α | ||
| + | | 1 | ||
| + | || 0 | ||
| + | |} | ||
| + | </td> | ||
| + | <td> | ||
| + | {| class="wikitable" style="text-align: center; width: 50px; height: 50px;" | ||
| + | |- | ||
| + | ! . | ||
| + | ! 0 | ||
| + | ! 1 | ||
| + | ! α | ||
| + | ! 1+α | ||
| + | |- | ||
| + | ! 0 | ||
| + | | 0 | ||
| + | | 0 | ||
| + | | 0 | ||
| + | || 0 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | α | ||
| + | || 1+α | ||
| + | |- | ||
| + | ! α | ||
| + | | 0 | ||
| + | | α | ||
| + | | 1+α | ||
| + | || 1 | ||
| + | |- | ||
| + | ! 1+α | ||
| + | | 0 | ||
| + | | 1+α | ||
| + | | 1 | ||
| + | || α | ||
| + | |} | ||
| + | </td> | ||
| + | </table> | ||
| + | Welche Bedeutung hat aber nun das neue Element <i>α</i>? | ||
| + | *Das Polynom <i>p</i>(<i>α</i>) = <i>α</i><sup>2</sup> + <i>α</i> + 1 hat keine Nullstelle in GF(2) = {0, 1}. Das bedeutet weiter, dass <i>α</i> weder 0 noch 1 sein kann.<br> | ||
| + | *Wäre <i>α</i> = 0 bzw. <i>α</i> = 1, so wären zudem zwei der vier Mengenelemente {0, 1, <i>α</i>, 1+<i>α</i>} jeweils identisch. Entweder „0” und „α” sowie „1” und „1+α” oder „1” und „α” sowie „0” und „1+α”.<br> | ||
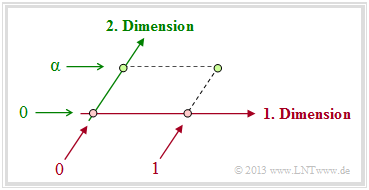
| + | *Vielmehr erhält der eindimensionale Körper GF(2) durch die Einführung des Elementes <i>α</i> eine zweite Dimension. Er wird also zum Galoisfeld GF(2<sup>2</sup>) erweitert, wie die folgende Grafik zeigt.<br> | ||
| + | :[[File:P ID2552 KC T 2 2 S1 v2.png|Übergang von GF(2) zu GF(2<sup>2</sup>) |class=fit]]<br> | ||
| + | *Das Element <i>α</i> hat ähnliche Bedeutung wie die imaginäre Einheit j, durch die man die Menge der reellen Zahlen unter der Nebenbedingung j<sup>2</sup> + 1 = 0 zur Menge der komplexen Zahlen erweitert.<br> | ||
| + | *Aufgrund der Identität <i>α</i><sup>2</sup> = 1 + <i>α</i>, die aus der Nebenbedingung <i>p</i>(<i>α</i>) = 0 folgt, kann man in gleicher Weise GF(2<sup>2</sup>) = {0, 1, <i>α</i>, <i>α</i><sup>2</sup>} schreiben, wobei nun folgende Operationstabellen gelten: | ||
| + | |||
| + | <html><style type="text/css">.paddingSpace td {padding:0 15px 0 15px;}</style></html> | ||
| + | <table class="paddingSpace"> | ||
| + | <td> | ||
| + | {| class="wikitable" style="text-align: center; width: 50px; height: 50px;" | ||
| + | |- | ||
| + | ! + | ||
| + | ! 0 | ||
| + | ! 1 | ||
| + | ! α | ||
| + | ! α<sup>2</sup> | ||
| + | |- | ||
| + | ! 0 | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | α | ||
| + | || α<sup>2</sup> | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 1 | ||
| + | | 0 | ||
| + | | α<sup>2</sup> | ||
| + | || α | ||
| + | |- | ||
| + | ! α | ||
| + | | α | ||
| + | | α<sup>2</sup> | ||
| + | | 0 | ||
| + | || 1 | ||
| + | |- | ||
| + | ! α<sup>2</sup> | ||
| + | | α<sup>2</sup> | ||
| + | | α | ||
| + | | 1 | ||
| + | || 0 | ||
| + | |} | ||
| + | </td> | ||
| + | <td> | ||
| + | {| class="wikitable" style="text-align: center; width: 50px; height: 50px;" | ||
| + | |- | ||
| + | ! . | ||
| + | ! 0 | ||
| + | ! 1 | ||
| + | ! α | ||
| + | ! α<sup>2</sup> | ||
| + | |- | ||
| + | ! 0 | ||
| + | | 0 | ||
| + | | 0 | ||
| + | | 0 | ||
| + | || 0 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | α | ||
| + | || α<sup>2</sup> | ||
| + | |- | ||
| + | ! α | ||
| + | | 0 | ||
| + | | α | ||
| + | | α<sup>2</sup> | ||
| + | || 1 | ||
| + | |- | ||
| + | ! α<sup>2</sup> | ||
| + | | 0 | ||
| + | | α<sup>2</sup> | ||
| + | | 1 | ||
| + | || α | ||
| + | |} | ||
| + | </td> | ||
| + | </table> | ||
Revision as of 23:48, 12 January 2017
GF(22) – Beispiel eines Erweiterungskörpers (1)
Im Kapitel 2.1 wurde bereits gezeigt, dass die endliche Zahlenmenge {0, 1, 2, 3} ⇒ q = 4 nicht die Eigenschaften eines Galoisfeldes GF(4) erfüllt. Vielmehr ergeben sich für die Addition modulo 4 und die Multiplikation modulo 4 folgende Tabellen:
\[{\rm Operationen } \hspace{0.15cm}{\rm modulo}\hspace{0.15cm}{\it q} = 4 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}\]
|
|
Für zi = 2 gibt es keine multiplikative Inverse InvM(zi). Dies erkennt man daran, dass kein einziges Element zj ∈ {0, 1, 2, 3} die Bedingung 2 · zj = 1 erfüllt. Geht man dagegen vom binären Galoisfeld GF(2) = {0, 1} aus und erweitert dieses entsprechend der Gleichung
\[{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, \]
so ergibt sich die ebenfalls endliche Menge {0, 1, α, 1 + α} ⇒ die Ordnung ist weiterhin q = 4. Führt man die Rechenoperationen modulo p(α) = α2 + α + 1 durch, so erhält man das folgende Ergebnis:
\[{\rm modulo} \hspace{0.15cm} {\it p} (\alpha) \hspace{0.25cm}\Rightarrow \]
|
|
Hierzu ist anzumerken:
- Die neutralen Elemente der Addition bzw. Multiplikation sind weiterhin NA = 0 und NM = 1.
- Da bei Modulo–Ausführung kein Unterschied zwischen Addition und Subtraktion besteht, ist α + α = α – α = 0. Für alle zi gilt somit: Die additive Inverse von zi ist das Element zi selbst.
- Die Einträge in der Multiplikationstabelle ergeben sich nach folgenden Berechnungen:
- \[\big [ \alpha \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 + \alpha) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1\hspace{0.05cm},\]
- \[\big [ \alpha \cdot \alpha \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 ) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1+\alpha\hspace{0.05cm},\]
- \[\big [ (1+\alpha) \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 + 1) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= \alpha\hspace{0.05cm}.\]
- Damit existieren für alle Elemente mit Ausnahme des Nullelements die multiplikativen Inversen:
- \[{\rm Inv_M}( 1) = 1 \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(\alpha) = 1+\alpha \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(1+\alpha) = \alpha \hspace{0.05cm}.\]
Daraus folgt: Die Menge {0, 1, α, 1 + α} stellt zusammen mit den zwei Rechenoperationen Addition und Multiplikation modulo p(α) = α2 + α + 1 ein Galoisfeld der Ordnung q = 4 dar. Dieses mit GF(22) = GF(4) bezeichnete Galoisfeld erfüllt alle in Kapitel 2.1 genannten Eigenschaften.
Im Gegensatz zum Zahlenkörper GF(3) = {0, 1, 2} mit der Eigenschaft, dass q = 3 eine Primzahl ist, nennt man GF(22) einen Erweiterungskörper (englisch: Extension Field).
GF(22) – Beispiel eines Erweiterungskörpers (2)
Das Polynom p(α) und damit die Bestimmungsgleichung p(α) = 0 darf nicht beliebig vorgegeben werden. Zum Beleg hierfür vergleichen wir die Verknüpfungstabellen für zwei verschiedene Polynome.
Polynom entsprechend der letzten Seite ⇒ p(α) = α2 + α + 1:
|
|
Neuer (allerdings ungeeigneter) Ansatz ⇒ p(α) = α2 + 1:
|
|
Die Additionstabelle ist in beiden Fällen identisch und auch die Multiplikationstabellen unterscheiden sich nur durch die vier Einträge in den beiden unteren Zeilen und den beiden hinteren Spalten:
- Aus p(α) = 0 folgt nun für das Produkt α · α = 1 und das Produkt (1+α) · (1+α) ergibt das Element 0. Das gemischte Produkt α · (1+α) ist nun 1+α.
- In der letzten Zeile der Multipliaktionstabelle und auch in der letzten Spalte steht nun keine „1” ⇒ Hinsichtlich der Bedingung p(α) = α2 + 1 = 0 existiert die multiplikative Inverse zu 1+α nicht.
- Damit erfüllt aber die endliche Menge {0, 1, α, 1+α} zusammen mit Rechenoperationen modulo p(α) = α2 + 1 auch nicht die Voraussetzungen eines Erweiterungskörpers GF(22).
Fassen wir zusammen: Aus dem binären Galoisfeld GF(2) = {0, 1} lässt sich unter Zuhilfenahme eines Polynoms vom Grad m = 2 mit binären Koeffizienten,
\[p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} \hspace{0.05cm},\]
ein Erweiterungskörper GF(22) formulieren. Im vorliegenden Fall gibt es nur ein geeignetes Polynom p1(x) = x2 + x + 1. Alle anderen möglichen Polynome vom Grad m = 2, nämlich
\[p_2(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},\] \[p_3(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},\] \[p_4(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^2 + x = (x+1) \cdot x \]
lassen sich faktorisieren und ergeben keinen Erweiterungskörper. Man nennt die Polynome p2(x), p3(x) und p4(x) reduzibel.
Anmerkung: Die Umbenennung der Funktionsvariablen α in x hat nur formale Bedeutung im Hinblick auf die folgenden Seiten.
GF(22) – Beispiel eines Erweiterungskörpers (3)
Wir betrachten weiterhin den Körper GF(22) = {0, 1, α, 1+α} entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung p(α) = α2 + α + 1 = 0 (irreduzibles Ploynom):
|
|
Welche Bedeutung hat aber nun das neue Element α?
- Das Polynom p(α) = α2 + α + 1 hat keine Nullstelle in GF(2) = {0, 1}. Das bedeutet weiter, dass α weder 0 noch 1 sein kann.
- Wäre α = 0 bzw. α = 1, so wären zudem zwei der vier Mengenelemente {0, 1, α, 1+α} jeweils identisch. Entweder „0” und „α” sowie „1” und „1+α” oder „1” und „α” sowie „0” und „1+α”.
- Vielmehr erhält der eindimensionale Körper GF(2) durch die Einführung des Elementes α eine zweite Dimension. Er wird also zum Galoisfeld GF(22) erweitert, wie die folgende Grafik zeigt.
- Das Element α hat ähnliche Bedeutung wie die imaginäre Einheit j, durch die man die Menge der reellen Zahlen unter der Nebenbedingung j2 + 1 = 0 zur Menge der komplexen Zahlen erweitert.
- Aufgrund der Identität α2 = 1 + α, die aus der Nebenbedingung p(α) = 0 folgt, kann man in gleicher Weise GF(22) = {0, 1, α, α2} schreiben, wobei nun folgende Operationstabellen gelten:
|
|