Difference between revisions of "Channel Coding/Algebraic and Polynomial Description"
| Line 92: | Line 92: | ||
::<math>\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} | ::<math>\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} | ||
\underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.</math>{{end}}<br> | \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.</math>{{end}}<br> | ||
| + | |||
| + | == Generatormatrix für Faltungscodierer der Rate 1/n == | ||
| + | <br> | ||
| + | Wir betrachten nun den Sonderfall <i>k</i> = 1, zum einen aus Gründen einer möglichst einfachen Darstellung, aber auch, weil Faltungscodierer der Rate 1/<i>n</i> für die Praxis eine große Bedeutung besitzen.<br><br> | ||
| + | |||
| + | [[File:P ID2602 KC T 3 2 S3a.png|rahmenlos|rechts|Faltungscoder (<i>k</i> = 1, <i>n</i> = 2, <i>m</i> = 1)]] | ||
| + | |||
| + | <b>Faltungscodierer mit <i>k</i> = 1, <i>n</i> = 2 und <i>m</i> = 1</b><br> | ||
| + | |||
| + | Aus der nebenstehenden Skizze kann abgeleitet werden: | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | ||
| + | 1 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}_1=\begin{pmatrix} | ||
| + | 0 & 1 | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | :<math>\Rightarrow \hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}=\begin{pmatrix} | ||
| + | 11 & 01 & 00 & 00 & 00 & \cdots & \\ | ||
| + | 00 & 11 & 01 & 00 & 00 & \cdots & \\ | ||
| + | 00 & 00 & 11 & 01 & 00 & \cdots & \\ | ||
| + | 00 & 00 & 00 & 11 & 01 & \cdots & \\ | ||
| + | \cdots & \cdots & \cdots & \cdots & \cdots & \cdots | ||
| + | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Für die Eingangssequenz <u><i>u</i></u> = (1, 0, 1, 1) beginnt die Codesequenz mit <u><i>x</i></u> = (1, 1, 0, 1, 1, 1, 1, 0, ...). Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Gewneratormatrix.<br><br> | ||
| + | |||
| + | [[File:P ID2603 KC T 3 2 S3b.png|rahmenlos|rechts|Faltungscoder (<i>k</i> = 1, <i>n</i> = 2, <i>m</i> = 2)]] | ||
| + | |||
| + | <b>Faltungscodierer mit <i>k</i> = 1, <i>n</i> = 2 und <i>m</i> = 2</b><br> | ||
| + | |||
| + | Aufgrund der Gedächtnisordnung <i>m</i> = 2 gibt es hier drei Teilmatrizen: | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | ||
| + | 1 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}_1=\begin{pmatrix} | ||
| + | 1 & 0 | ||
| + | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}_2=\begin{pmatrix} | ||
| + | 1 & 1 | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | :<math>\Rightarrow \hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}=\begin{pmatrix} | ||
| + | 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ | ||
| + | 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ | ||
| + | 00 & 00 & 11 & 10 & 11 & 00 & \cdots & \\ | ||
| + | 00 & 00 & 00 & 11 & 10 & 11 & \cdots & \\ | ||
| + | \cdots & \cdots & \cdots & \cdots & \cdots & \cdots | ||
| + | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Hier führt die Eingangsssequenz <u><i>u</i></u> = (1, 0, 1, 1) zur Codesequenz <u><i>x</i></u> = (1, 1, 1, 0, 0, 0, 0, 1, ...).<br><br> | ||
| + | |||
| + | [[File:P ID2604 KC T 3 2 S3c.png|rahmenlos|rechts|Faltungscoder (<i>k</i> = 1, <i>n</i> = 3, <i>m</i> = 3)]] | ||
| + | |||
| + | <b>Faltungscodierer mit <i>k</i> = 1, <i>n</i> = 3 und <i>m</i> = 3</b> | ||
| + | |||
| + | Wegen <i>m</i> = 3 gibt es vier Teilmatrizen der Dimension 1 × 3: | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | ||
| + | 1 & 1 & 0 | ||
| + | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}_1=\begin{pmatrix} | ||
| + | 0 & 0 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm},</math> | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm G}}_2=\begin{pmatrix} | ||
| + | 0 & 0 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| + | { \boldsymbol{\rm G}}_3=\begin{pmatrix} | ||
| + | 0 & 1 & 1 | ||
| + | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| + | |||
| + | Damit lautet die resultierende Generatormatrix: | ||
| + | |||
| + | :<math>{ \boldsymbol{\rm G}}=\begin{pmatrix} | ||
| + | 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ | ||
| + | 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ | ||
| + | 000 & 000 & 110 & 001 & 001 & 011 & 000 & \cdots & \\ | ||
| + | 000 & 000 & 000 & 110 & 001 & 001 & 011 & \cdots & \\ | ||
| + | \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots | ||
| + | \end{pmatrix}\hspace{0.05cm},</math> | ||
| + | |||
| + | und man erhält für <u><i>u</i></u> = (1, 0, 1, 1) die Codesequenz <u><i>x</i></u> = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, ...).<br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 15:39, 15 January 2017
Definition und Interpretation der Teilmatrizen G0, ... , Gm
Entsprechend den Ausführungen in Kapitel 1.4 lässt sich das Codewort x eines linearen Blockcodes aus dem Informationswort u und der Generatormatrix G in einfacher Weise ermitteln:
\[\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]
Dabei gilt:
- Die Vektoren u und x haben die Länge k (Bitanzahl eines Informationswortes) bzw. n (Bitanzahl eines Codewortes) und G besitzt die Dimension k × n (k Zeilen und n Spalten).
- Bei Faltungscodierung bezeichnen dagegen u und x Sequenzen mit k' → ∞ und n' → ∞. Deshalb wird auch die Generatormatrix G in beiden Richtungen unendlich weit ausgedehnt sein.
Als Vorbereitung für die Einführung der Generatormatrix G auf der nächsten Seite definieren wir m + 1 Teilmatrizen, jeweils mit k Zeilen und n Spalten, die wir mit Gl bezeichnen, wobei 0 ≤ l ≤ m gilt.
Diese Definition wird nun an einem Beispiel verdeutlicht.
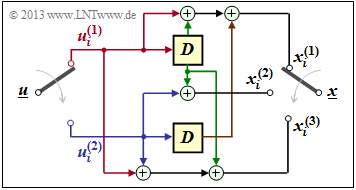 Wir betrachten wiederum den Faltungscodierer gemäß nebenstehender Grafik mit den folgenden Codebits:
Wir betrachten wiederum den Faltungscodierer gemäß nebenstehender Grafik mit den folgenden Codebits:
\[x_i^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\] \[x_i^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\] \[x_i^{(3)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]
Wegen der Gedächtnisordnung m = 1 wird dieser Codierer durch die beiden Teilmatrizen G0 und G1 charakterisiert:
\[{ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]
Diese Matrizen sind wie folgt zu interpretieren:
- Erste Zeile von G0, rote Pfeile: ui(1) beeinflusst sowohl xi(1) als auch xi(3), nicht jedoch xi(2).
- Zweite Zeile von G0, blaue Pfeile: ui(2) beeinflusst xi(2) und xi(3), aber nicht xi(1).
- Erste Zeile von G1, grüne Pfeile: ui–1(1) beeinflusst alle drei Coderausgänge.
- Zweite Zeile von G1, brauner Pfeil: ui–1(2) beeinflusst nur xi(1).
Generatormatrix eines Faltungscodierers mit Gedächtnis m
Mit den Teilmatrizen G0, ... , Gm lassen sich die n Codebits zum Zeitpunkt i wie folgt ausdrücken:
\[\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 + ... + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m \hspace{0.05cm}.\]
Hierbei sind folgende vektorielle Größen zu berücksichtigen:
\[\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.\]
Betrachtet man die bei i = 1 beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen
\[\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\]
so kann dieser Zusammenhang durch die Matrixgleichung x = u · G ausgedrückt werden. Hierbei ist für die Generatormatrix G zu setzen:
\[{ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \cdots & \cdots & & & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Aus der Gleichung erkennt man sofort das Gedächtnis m des Faltungscodes. Die Parameter k und n sind direkt nicht ablesbar. Sie sind aber durch die Zeilen– und Spaltenzahl der Teilmatrizen Gl festgelegt.
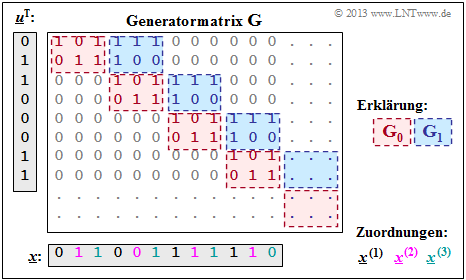 Mit den zwei Matrizen G0 und G1 – siehe letztes Beispiel – erhält man die rechts skizzierte Matrix G.
Mit den zwei Matrizen G0 und G1 – siehe letztes Beispiel – erhält man die rechts skizzierte Matrix G.
Anzumerken ist:
- Die Generatormatrix G erstreckt sich nach unten und nach rechts eigentlich bis ins Unendliche. Explizit dargestellt sind aber nur 8 Zeilen und 12 Spalten.
- Für die zeitlich begrenzte Informationssequenz u = (0, 1, 1, 0, 0, 0, 1, 1) ist der gezeichnete Matrixteil ausreichend. Die Codesequenz lautet dann: x = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0).
- Anhand der Beschriftungsfarben lassen sich die n = 3 Codewortstränge ablesen. Das gleiche Ergebnis haben wir (auf anderem Wege) im Beispiel am Ende von Kapitel 3.1 erhalten.
- \[\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.\]
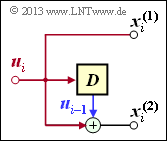
Generatormatrix für Faltungscodierer der Rate 1/n
Wir betrachten nun den Sonderfall k = 1, zum einen aus Gründen einer möglichst einfachen Darstellung, aber auch, weil Faltungscodierer der Rate 1/n für die Praxis eine große Bedeutung besitzen.
Faltungscodierer mit k = 1, n = 2 und m = 1
Aus der nebenstehenden Skizze kann abgeleitet werden:
\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 1 \end{pmatrix}\]
\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 01 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 01 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 01 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 01 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Für die Eingangssequenz u = (1, 0, 1, 1) beginnt die Codesequenz mit x = (1, 1, 0, 1, 1, 1, 1, 0, ...). Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Gewneratormatrix.
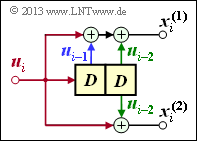
Faltungscodierer mit k = 1, n = 2 und m = 2
Aufgrund der Gedächtnisordnung m = 2 gibt es hier drei Teilmatrizen:
\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_2=\begin{pmatrix} 1 & 1 \end{pmatrix}\]
\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 10 & 11 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 10 & 11 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Hier führt die Eingangsssequenz u = (1, 0, 1, 1) zur Codesequenz x = (1, 1, 1, 0, 0, 0, 0, 1, ...).
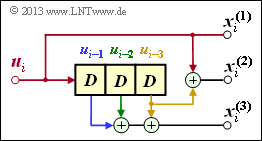
Faltungscodierer mit k = 1, n = 3 und m = 3
Wegen m = 3 gibt es vier Teilmatrizen der Dimension 1 × 3:
\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]
\[{ \boldsymbol{\rm G}}_2=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_3=\begin{pmatrix} 0 & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]
Damit lautet die resultierende Generatormatrix:
\[{ \boldsymbol{\rm G}}=\begin{pmatrix} 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ 000 & 000 & 110 & 001 & 001 & 011 & 000 & \cdots & \\ 000 & 000 & 000 & 110 & 001 & 001 & 011 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm},\]
und man erhält für u = (1, 0, 1, 1) die Codesequenz x = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, ...).