Aufgaben:Exercise 3.3Z: Rectangular Pulse and Dirac Delta

• Return to book

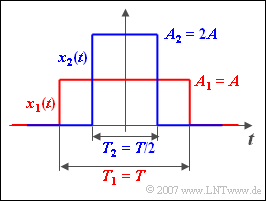
Wir betrachten hier eine Vielzahl von symmetrischen Rechteckfunktionen $x_k(t)$. Die Rechtecke unterscheiden sich durch unterschiedliche Amplituden (Höhen)

$$A_k = k \cdot A$$

und unterschiedliche Impulsdauern (Breiten)

$$T_k = T/k.$$

Hierbei sei k ein beliebiger positiver Wert. Der im Bild rot dargestellte Rechteckimpuls $x_1(t)$ hat die Amplitude $A_1 = \text{A} = 2 \text{V}$ und die Dauer $T_1 = \text{T} = 500 \text{$\mu$s}$. Der blau gezeichnete Impuls x2(t) ist halb so breit ($T_2 = 250 \text{$\mu$s}$), aber doppelt so hoch ($A_2 = 4 \text{V}$).

Hinweise:

• Die Aufgabe gehört zum Kapitel Einige Sonderfälle impulsartiger Signale.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gegeben sind weiterhin folgende trigonometrischen Umformungen:

$$\sin ^2( \alpha ) = {1}/{2} \cdot \left( {1 - \cos ( {2\alpha } )} \right),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.2. Sie können Ihre Ergebnisse anhand zweier Interaktionsmodule überprüfen:

• Zeitfunktion und zugehörige Spektralfunktion

• Frequenzgang und zugehörige Impulsantwort

Fragebogen

1

Welche der folgenden Aussagen treffen bezüglich des Spektrums $X_1(f)$ zu?

	Der Spektralwert $X_1(f = 0)$ ist gleich $10^{–3} \text{V/Hz}$.
	$X_1(f)$ besitzt Nullstellen im Abstand von $2 \text{kHz}$.
	$X_1(f)$ besitzt Nullstellen im Abstand von $4 \text{kHz}$.

2

Welche der folgenden Aussagen treffen bezüglich des Spektrums $X_2(f)$ zu?

	Der Spektralwert $X_2(f = 0)$ ist gleich $10^{–3} \text{V/Hz}$.
	$X_2(f)$ besitzt Nullstellen im Abstand von $2 \text{kHz}$.
	$X_2(f)$ besitzt Nullstellen im Abstand von $4 \text{kHz}$.

3

Es gelte $k = 10$. Berechnen Sie die Frequenz $f_10$ der ersten Nullstelle und den Spektralwert bei $f = 2 \text{kHz}$.

$f_{10}$ = $\text{kHz}$

$X_{10}(f = 2 \text{kHz})$ = $\cdot 10^{-3}\ \text{V/Hz}$

4

Wie groß wird der Spektralwert bei $f = 2 \text{kHz}$ im Grenzfall $k \rightarrow \infty$? Interpretieren Sie das Ergebnis.

$X_{\infty}(f = 2 \text{kHz}$ = $\cdot 10^{-3}\ \text{V/Hz}$

Musterlösung

Solution

1. Der Spektralwert bei der Frequenz $f = 0$ ist nach dem ersten Fourierintegral stets gleich der Fläche unter der Zeitfunktion:

$$X( f ) = \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm{e}}^{ - {\rm{j2\pi }}ft} \hspace{0.1cm} {\rm d}t \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \;X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t )}\hspace{0.1cm} {\rm d}t.$$

Im vorliegenden Fall ist die Impulsfläche stets $A \cdot T = 10^{–3} \text{Vs} = 10^{–3} \text{V/Hz}$. Wegen $T_1 = 500 \text{$\mu$s}$ weist das Spektrum $X_1(f)$ Nulldurchgänge im Abstand $f_1 = 1/T_1 = 2 \text{kHz}$ auf.

Richtig sind somit die Lösungsvorschläge 1 und 2.

2. Aufgrund gleicher Impulsflächen wird der Spektralwert bei der Frequenz $f = 0$ nicht verändert. Die äquidistanten Nulldurchgänge treten nun im Abstand $f_2 = 1/T_2 = 4 \text{kHz}$ auf. Richtig sind somit die Lösungsvorschläge 1 und 3.

3. Nullstellen gibt es bei Vielfachen von $f_{10} = 1/T_{10} = 20 \text{kHz}$, und die Spektralfunktion lautet:

$$X_{10} ( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}f/f_{10} } ).$$

Bei der Frequenz $f = 2 \text{kHz}$ ist das Argument der si-Funktion gleich $\pi/10$ (oder $18°$):

$$X_{10} ( {f = 2\;{\rm{kHz}}}) = 10^{ - 3} \;{\rm{V/Hz}} \cdot \frac{{\sin ( {18^\circ } )}}{{{\rm{\pi /10}}}} \hspace{0.15 cm}\underline{= 0.984 \cdot 10^{ - 3} \;{\rm{V/Hz}}}{\rm{.}}$$

4. Im Grenzfall $k \rightarrow \infty$ geht der dann unendlich hohe und unendlich schmale Rechteckimpuls in den Diracimpuls über. Dessen Spektrum ist für alle Frequenzen konstant. Damit gilt auch bei der Frequenz $f = 2 \text{kHz}$ der Spektralwert $10^{–3} \text{V/Hz}$.