Aufgaben:Exercise 3.5: Differentiation of a Triangular Pulse

• Return to book

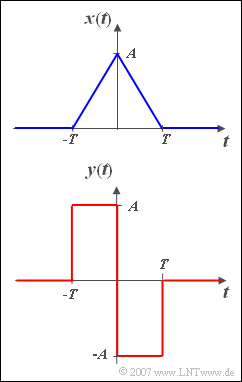
Gesucht wird das Spektrum $Y(f)$ des Signals

$$y\left( t \right) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f \ddot{u}r}}} \\ {{\rm{f\ddot{u} r}}} \\ {{\rm{f\ddot{u}r}}} \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {{\rm{sonst}}{\rm{.}}} \\\end{array}$$

Dabei gelte $A = 1\,{\rm V}$ und $T = 0.5\,{\rm ms}$.

Als bekannt vorausgesetzt wird die Fouriertransformierte des oben skizzierten Dreieckimpulses $x(t)$, nämlich

$$X( f ) = A \cdot T \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }}fT} ),$$

wobei wiederum $\text{si}(x) = \text{sin}(x)/x$ gilt.

Ein Vergleich der beiden Zeitsignale zeigt, dass zwischen den Funktionen $x(t)$ und $y(t)$ folgender Zusammenhang besteht:

$$y(t) = T \cdot \frac{{{\rm d}x(t)}}{{{\rm d}t}}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
• Alle dort dargelegten Gesetzmäßigkeiten – unter Anderem auch der Verschiebungssatz und der Integrationssatz – werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation (Dauer Teil 1: 5:57 – Teil 2: 5:55) an Beispielen verdeutlicht.
• In der Teilaufgabe (3) soll das Spektrum $Y(f)$ ausgehend von einem symmetrischen Rechteckimpuls $r(t)$ mit Amplitude $A$ und Dauer $T$ sowie dessen Spektrum $R(f) = A \cdot T \cdot \text{si}(\pi fT)$ berechnet werden. Dies erreicht man durch zweimalige Anwendung des Verschiebungssatzes.
• In der Aufgabe 3.5Z wird das gleiche Spektrum $Y(f)$ ausgehend von einem aus drei Diracfunktionen bestehenden Signal durch Anwendung des Integrationssatzes berechnet.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie die Spektralfunktion $Y(f)$ am Ausgang. Wie groß ist deren Betrag bei den Frequenzen $f$ = 0 bzw. $f$ = 1 kHz?

$|Y(f=0)| =$ mV/Hz

$|Y(f=1 \text{kHz})| =$ mV/Hz

2

Welche Aussagen sind hinsichtlich des Spektrums $Y(f)$ zutreffend?

+ Die Nullstellen von $X(f)$ bleiben auch in $Y(f)$ erhalten.

- Für $f$ → $\infty$ hat $Y(f)$ den gleichen Verlauf wie $X(f)$.

+ Für $f$ → $\infty$ ist $Y(f)$ doppelt so groß wie beim Spektrum eines Rechteckimpulses der Dauer $T$.

3

Berechnen Sie $Y(f)$ ausgehend vom Rechteckimpuls durch Anwendung des Verschiebungssatzes. Welche Aussage ist bei diesem Beispiel zutreffend?

	Der Differentiationssatz führt hier schneller zum Ergebnis.
	Der Verschiebungssatz führt schneller zum Ergebnis.

Musterlösung

Solution

1. Der Differentiationssatz lautet allgemein:

$$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$

Angewandt auf das vorliegende Beispiel erhält man:

$$Y( f ) = T \cdot {\rm{j}}2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$

Diese Funktion ist rein imaginär. Bei der Frequenz $f$ = 0 verschwindet auch der Imaginärteil. Dies kann man z. B. durch Anwendung der Regel von l'Hospital formal nachweisen. Das Ergebnis folgt aber auch aus der Tatsache, dass der Spektralwert bei $f$ = 0 gleich dem Integral über die Zeitfunktion $y(t)$ ist. Bei der normierten Frequenz $f \cdot T$ = 0.5 (also für $f$ = 1 kHz) ist die Sinusfunktion gleich 1 und man erhält $|Y(f = 1 \text{kHz})| = 4/\pi \cdot A \cdot T$, also näherungsweise $0.636 cdot 10^{–3}$ V/Hz (positiv imaginär).

2. Die Nullstellen von $X(f)$ bleiben erhalten und es gibt eine weitere Nullstelle bei der Frequenz $f$ = 0. Als asymptotischen Verlauf bezeichnet man die obere Schranke

$$\left| {Y_{\max }( f )} \right| = \frac[[:Template:2A]]{{{\rm{\pi }\cdot }|f|}} \ge \left| {Y( f )} \right|.$$

Für die Frequenzen, bei denen die Sinusfunktion die Werte ±1 liefert, sind $|Y_{\text{max}}(f)|$ und $|Y(f)|$ identisch. Beim Rechteckimpuls der Amplitude $A$ lautet die entsprechende Schranke $A/(\pi \cdot |f|)$. Dagegen fällt das Spektrum $X(f)$ des Dreieckimpulses asymptotisch schneller ab:

$$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$

Dies ist darauf zurückzuführen, dass x(t) keine Unstetigkeitsstellen aufweist. Richtig sind demnach die Lösungsvorschläge 1 und 3.

3. Ausgehend von einem symmetrischen Rechteckimpuls $r(t)$ mit Amplitude $A$ und Dauer $T$ kann das Signal $y(t)$ auch wie folgt dargestellt werden:

$$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$

Durch zweimalige Anwendung des Verschiebungssatzes erhält man:

$$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$

Mit der Beziehung $e^{\text{j}x} – e^{–\text{j}x} = 2\text{j} \cdot \text{sin}(x)$ kann hierfür auch geschrieben werden:

$$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$

Es ergibt sich folgerichtig das gleiche Ergebnis wie unter Punkt 1). Welcher Weg schneller zum Ergebnis führt, muss jeder Einzelnen selbst für sich entscheiden. Die Autoren meinen, dass der erste Weg etwas günstiger ist. Subjektiv entscheiden wir uns für den Lösungsvorschlag 1.