Difference between revisions of "Aufgaben:Exercise 4.4Z: Pointer Diagram for SSB-AM"
| Line 58: | Line 58: | ||
j}\hspace{0.05cm} \omega_{\rm 60} \hspace{0.05cm} t }.$$ | j}\hspace{0.05cm} \omega_{\rm 60} \hspace{0.05cm} t }.$$ | ||
Zum Zeitpunkt $t = 0$ nehmen die komplexen Exponentialfunktionen jeweils den Wert $1$ an und man erhält $\text{Re}[s_+(t = 0)] \; \underline{= 1\ \text{V}}$ und $\text{Im}[s_+(t = 0)]\; \underline{ = \,–\hspace{-0.08cm}1\ \text{V}}$ (siehe linke Grafik). | Zum Zeitpunkt $t = 0$ nehmen die komplexen Exponentialfunktionen jeweils den Wert $1$ an und man erhält $\text{Re}[s_+(t = 0)] \; \underline{= 1\ \text{V}}$ und $\text{Im}[s_+(t = 0)]\; \underline{ = \,–\hspace{-0.08cm}1\ \text{V}}$ (siehe linke Grafik). | ||
| + | |||
| + | [[File:P_ID733__Sig_Z_4_4_ML.png|center|Drei verschiedene analytische Signale]] | ||
| − | |||
'''2.''' Für das analytische Signal kann auch geschrieben werden: | '''2.''' Für das analytische Signal kann auch geschrieben werden: | ||
:$$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot \cos({ \omega_{\rm | :$$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot \cos({ \omega_{\rm | ||
| Line 73: | Line 74: | ||
50}\hspace{0.05cm} t }) + {\rm 1 \hspace{0.05cm} V} \cdot \sin({ | 50}\hspace{0.05cm} t }) + {\rm 1 \hspace{0.05cm} V} \cdot \sin({ | ||
\omega_{\rm 60}\hspace{0.05cm} t }).$$ | \omega_{\rm 60}\hspace{0.05cm} t }).$$ | ||
| − | Bei alleiniger Berücksichtigung des $50 \ \text{kHz-Cosinussignals}$ würde der erste Nulldurchgang bei $t_1 = T_0/4$ auftreten, also nach $5 \ \mu \text{s}$, wobei $T_0 = 1/f_{50} = 20 \ \mu \text{s}$ die Periodendauer dieses Signals bezeichnet. Das Sinussignal mit der Frequenz $60 \ \text{ kHz}$ ist während der gesamten ersten Halbwelle ($0 ... 8.33\ \mu \text{s}$) positiv. Aufgrund des Pluszeichens verzögert sich der erste Nulldurchgang von $s(t) \Rightarrow t_1 > 5\ \mu \text{s}$. Richtig ist also der <u>Lösungsvorschlag 3</u>. | + | Bei alleiniger Berücksichtigung des $50 \ \text{kHz-Cosinussignals}$ würde der erste Nulldurchgang bei $t_1 = T_0/4$ auftreten, also nach $5 \ \mu \text{s}$, wobei $T_0 = 1/f_{50} = 20 \ \mu \text{s}$ die Periodendauer dieses Signals bezeichnet. Das Sinussignal mit der Frequenz $60 \ \text{ kHz}$ ist während der gesamten ersten Halbwelle ($0 \, ... \, 8.33\ \mu \text{s}$) positiv. Aufgrund des Pluszeichens verzögert sich der erste Nulldurchgang von $s(t) \Rightarrow t_1 > 5\ \mu \text{s}$. Richtig ist also der <u>Lösungsvorschlag 3</u>. |
Die mittlere Grafik zeigt das analytische Signal zum Zeitpunkt $t = T_0/4$, zu dem der rote Träger seinen Nulldurchgang hätte. Der Nulldurchgang des violetten Summenzeigers tritt erst dann auf, wenn dieser in Richtung der imaginären Achse zeigt. Dann gilt $s(t_1) = \text{Re}[s_+(t_1)] = 0$. | Die mittlere Grafik zeigt das analytische Signal zum Zeitpunkt $t = T_0/4$, zu dem der rote Träger seinen Nulldurchgang hätte. Der Nulldurchgang des violetten Summenzeigers tritt erst dann auf, wenn dieser in Richtung der imaginären Achse zeigt. Dann gilt $s(t_1) = \text{Re}[s_+(t_1)] = 0$. | ||
| − | |||
| − | Dieser Fall wird zum ersten Mal dann erreicht, wenn der schnellere Zeiger mit der Winkelgeschwindigkeit $\omega_{60}$ seinen „Rückstand” von $ | + | '''3.''' Der Maximalwert von $|s_+(t)|$ wird erreicht, wenn beide Zeiger in die gleiche Richtung weisen. Der Betrag des Summenzeigers ist dann gleich der Summe der beiden Einzelzeiger; also $\underline {2\ \text{ V}}$. |
| − | :$$\omega_{\rm 60}\ | + | |
| − | 50}\ | + | Dieser Fall wird zum ersten Mal dann erreicht, wenn der schnellere Zeiger mit der Winkelgeschwindigkeit $\omega_{60}$ seinen „Rückstand” von $90^{\circ} \; (\pi /2)$ gegenüber dem langsameren Zeiger ($\omega_{50}$) aufgeholt hat: |
| + | :$$\omega_{\rm 60} \cdot t_2 - \omega_{\rm | ||
| + | 50}\cdot t_2 = \frac{\pi}{2} \hspace{0.3cm} | ||
\Rightarrow\hspace{0.3cm}t_2 = \frac{\pi/2}{2\pi (f_{\rm 60}- | \Rightarrow\hspace{0.3cm}t_2 = \frac{\pi/2}{2\pi (f_{\rm 60}- | ||
f_{\rm 50})} = \frac{1}{4 | f_{\rm 50})} = \frac{1}{4 | ||
| Line 87: | Line 89: | ||
Zu diesem Zeitpunkt haben die beiden Zeiger $5/4$ bzw. $6/4$ Umdrehungen zurückgelegt und weisen beide in Richtung der imaginären Achse (siehe rechte Grafik). Das tatsächliche Signal $s(t)$ – also der Realteil von $s_+(t)$ – ist deshalb in diesem Moment gleich $0$. | Zu diesem Zeitpunkt haben die beiden Zeiger $5/4$ bzw. $6/4$ Umdrehungen zurückgelegt und weisen beide in Richtung der imaginären Achse (siehe rechte Grafik). Das tatsächliche Signal $s(t)$ – also der Realteil von $s_+(t)$ – ist deshalb in diesem Moment gleich $0$. | ||
| − | '''4.''' | + | '''4.''' Bedingung für $|s_+(t_3)| = 0$ ist, dass zwischen den beiden gleich langen Zeigern ein Phasenversatz von $180^\circ$ besteht, sodass sie sich auslöschen. Dies bedeutet weiter, dass der schnellere Zeiger um $3\pi /2$ weiter gedreht hat als der $50 \ \text{kHz-Anteil}$. Analog zur Musterlösung der Teilaufgabe (3) gilt deshalb: |
:$$t_3 = \frac{3\pi/2}{2\pi (f_{\rm 60}- f_{\rm 50})} \hspace{0.15 cm}\underline{= | :$$t_3 = \frac{3\pi/2}{2\pi (f_{\rm 60}- f_{\rm 50})} \hspace{0.15 cm}\underline{= | ||
{\rm 75 \hspace{0.05cm} \mu s}}.$$ | {\rm 75 \hspace{0.05cm} \mu s}}.$$ | ||
Revision as of 14:39, 20 January 2017
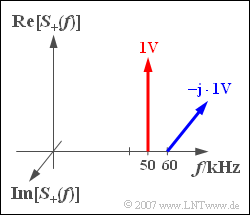
Betrachtet werden soll das analytische Signal $s_+(t)$ mit dem Linienspektrum
- $$S_{+}(f) = {\rm 1 \hspace{0.05cm} V} \cdot\delta (f - f_{\rm 50})- {\rm j} \cdot {\rm 1 \hspace{0.05cm} V} \cdot\delta (f - f_{\rm 60}).$$
Hierbei stehen $f_{50}$ und $f_{60}$ als Abkürzungen für die Frequenzen $50 \ \text{kHz}$ bzw. $60 \ \text{kHz}$.
Dieses analytische Signal könnte zum Beispiel bei der Einseitenband–Amplitudenmodulation (ESB-AM) eines sinusförmigen Nachrichtensignals (Frequenz $f_{\rm N} = 10 \ \text{kHz}$) mit einem cosinusförmigen Trägersignal ($f_{\rm T} = 50 \ \text{kHz}$) auftreten, wobei nur das obere Seitenband übertragen wird (OSB-Modulation).
Das analytische Signal könnte aber auch durch eine USB-Modulation des gleichen Sinussignals entstehen, wenn ein sinusförmiges Trägersignal mit der Trägerfrequenz $f_{\rm T} = 60 \ \text{kHz}$ verwendet wird.
Hinweise:
- Die Aufgabe gehört zum Kapitel Analytisches Signal und zugehörige Spektralfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Sie können Ihre Lösung mit dem Interaktionsmodul Zeigerdiagramm – Darstellung des analytischen Signals überprüfen.
Fragebogen
Musterlösung
- $$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 50}\hspace{0.05cm} t } - {\rm j}\cdot{\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 60} \hspace{0.05cm} t }.$$
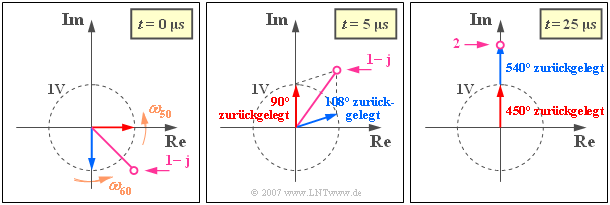
Zum Zeitpunkt $t = 0$ nehmen die komplexen Exponentialfunktionen jeweils den Wert $1$ an und man erhält $\text{Re}[s_+(t = 0)] \; \underline{= 1\ \text{V}}$ und $\text{Im}[s_+(t = 0)]\; \underline{ = \,–\hspace{-0.08cm}1\ \text{V}}$ (siehe linke Grafik).
2. Für das analytische Signal kann auch geschrieben werden:
- $$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot \cos({ \omega_{\rm 50}\hspace{0.05cm} t }) + {\rm j} \cdot{\rm 1 \hspace{0.05cm} V} \cdot \sin({ \omega_{\rm 50}\hspace{0.05cm} t })+\\ - {\rm j} \cdot {\rm 1 \hspace{0.05cm} V} \cdot \cos({ \omega_{\rm 60}\hspace{0.05cm} t }) + {\rm 1 \hspace{0.05cm} V} \cdot \sin({ \omega_{\rm 60}\hspace{0.05cm} t }).$$
Der Realteil hiervon beschreibt das tatsächliche, physikalische Signal:
- $$s(t) = {\rm 1 \hspace{0.05cm} V} \cdot \cos({ \omega_{\rm 50}\hspace{0.05cm} t }) + {\rm 1 \hspace{0.05cm} V} \cdot \sin({ \omega_{\rm 60}\hspace{0.05cm} t }).$$
Bei alleiniger Berücksichtigung des $50 \ \text{kHz-Cosinussignals}$ würde der erste Nulldurchgang bei $t_1 = T_0/4$ auftreten, also nach $5 \ \mu \text{s}$, wobei $T_0 = 1/f_{50} = 20 \ \mu \text{s}$ die Periodendauer dieses Signals bezeichnet. Das Sinussignal mit der Frequenz $60 \ \text{ kHz}$ ist während der gesamten ersten Halbwelle ($0 \, ... \, 8.33\ \mu \text{s}$) positiv. Aufgrund des Pluszeichens verzögert sich der erste Nulldurchgang von $s(t) \Rightarrow t_1 > 5\ \mu \text{s}$. Richtig ist also der Lösungsvorschlag 3.
Die mittlere Grafik zeigt das analytische Signal zum Zeitpunkt $t = T_0/4$, zu dem der rote Träger seinen Nulldurchgang hätte. Der Nulldurchgang des violetten Summenzeigers tritt erst dann auf, wenn dieser in Richtung der imaginären Achse zeigt. Dann gilt $s(t_1) = \text{Re}[s_+(t_1)] = 0$.
3. Der Maximalwert von $|s_+(t)|$ wird erreicht, wenn beide Zeiger in die gleiche Richtung weisen. Der Betrag des Summenzeigers ist dann gleich der Summe der beiden Einzelzeiger; also $\underline {2\ \text{ V}}$.
Dieser Fall wird zum ersten Mal dann erreicht, wenn der schnellere Zeiger mit der Winkelgeschwindigkeit $\omega_{60}$ seinen „Rückstand” von $90^{\circ} \; (\pi /2)$ gegenüber dem langsameren Zeiger ($\omega_{50}$) aufgeholt hat:
- $$\omega_{\rm 60} \cdot t_2 - \omega_{\rm 50}\cdot t_2 = \frac{\pi}{2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm}t_2 = \frac{\pi/2}{2\pi (f_{\rm 60}- f_{\rm 50})} = \frac{1}{4 \cdot(f_{\rm 60}- f_{\rm 50})}\hspace{0.15 cm}\underline{= {\rm 25 \hspace{0.05cm} \mu s}}.$$
Zu diesem Zeitpunkt haben die beiden Zeiger $5/4$ bzw. $6/4$ Umdrehungen zurückgelegt und weisen beide in Richtung der imaginären Achse (siehe rechte Grafik). Das tatsächliche Signal $s(t)$ – also der Realteil von $s_+(t)$ – ist deshalb in diesem Moment gleich $0$.
4. Bedingung für $|s_+(t_3)| = 0$ ist, dass zwischen den beiden gleich langen Zeigern ein Phasenversatz von $180^\circ$ besteht, sodass sie sich auslöschen. Dies bedeutet weiter, dass der schnellere Zeiger um $3\pi /2$ weiter gedreht hat als der $50 \ \text{kHz-Anteil}$. Analog zur Musterlösung der Teilaufgabe (3) gilt deshalb:
- $$t_3 = \frac{3\pi/2}{2\pi (f_{\rm 60}- f_{\rm 50})} \hspace{0.15 cm}\underline{= {\rm 75 \hspace{0.05cm} \mu s}}.$$