Theory of Stochastic Signals/Set Theory Basics

1. Theory of Stochastic Signals
2. Wahrscheinlichkeitsrechnung
3. Set Theory Basics

• Previous page
• Next page

• Previous page
• Next page

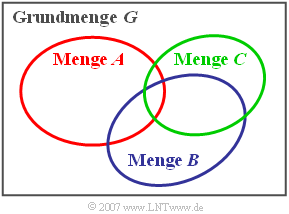
Venndiagramm, Grundmenge und leere Menge

In späteren Kapitel wird manchmal auf die 'Mengenlehre Bezug genommen. Deshalb sollen hier die wichtigsten Grundlagen und Definitionen dieser Disziplin kurz zusammengefasst werden.

Die Thematik wird auch im Lernvideo Mengentheoretische Begriffe und Gesetzmäßigkeiten am Beispiel europäischer Staaten behandelt:

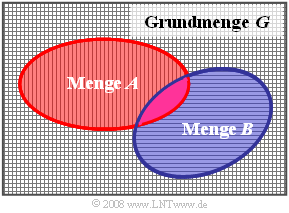
Ein wichtiges Hilfsmittel der Mengenlehre ist das Venndiagramm gemäß der obigen Grafik:

• Angewandt auf die Wahrscheinlichkeitsrechnung sind hier die Ereignisse $A_i$ als Flächenbereiche dargestellt. Zur einfacheren Beschreibung bezeichnen wir hier die Ereignisse im Gegensatz zum letzten Kapitel nicht mit $A_1$, $A_2$ und $A_3$, sondern mit $A$, $B$ und $C$. Die Gesamtfläche entspricht der Grundmenge $G$.
• Die Grundmenge $G$ beinhaltet alle möglichen Ergebnisse und steht für das Sichere Ereignis, das definitionsgemäß mit der Wahrscheinlichkeit „Eins” eintritt:   ${\rm Pr}(G) = 1$. Zum Beispiel ist beim Zufallsexperiment „Werfen eines Würfels” die Wahrscheinlichkeit für das Ereignis „die Augenzahl ist kleiner oder gleich 6” identisch 1.
• Dagegen beinhaltet die Leere Menge $ϕ$ kein einziges Element. Bezogen auf Ereignisse gibt die leere Menge das Unmögliche Ereignis mit der Wahrscheinlichkeit ${\rm Pr}(ϕ) = 0$ an. Beispielsweise ist beim Experiment „Werfen eines Würfels”' die Wahrscheinlichkeit für das Ereignis „die Augenzahl ist größer als 6” identisch 0.

Anzumerken ist, dass nicht jedes Ereignis $A$ mit ${\rm Pr}(A) = 0$ wirklich nie eintreten kann. So ist die Wahrscheinlichkeit des Ereignisses „der Rauschwert $n$ ist identisch $0$” zwar verschwindend klein und es gilt ${\rm Pr}(n \equiv 0) = 0$, wenn $n$ durch eine kontinuierliche Zufallsgröße beschrieben wird. Trotzdem ist es natürlich möglich, dass irgendwann auch der exakte Rauschwert $n = 0$ auftritt.

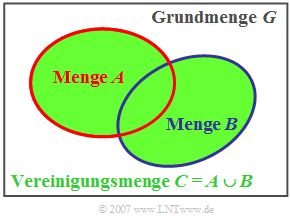
Vereinigungsmenge

Anhand des Venndiagramms werden nun einige mengentheoretische Verknüpfungen erläutert.

Die Vereinigungsmenge $C$ zweier Mengen $A$ und $B$ beinhaltet alle die Elemente, die entweder in der Menge $A$ oder der Menge $B$ oder in beiden enthalten sind (englisch: Set Union ). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: $$\ C = A \cup B \hspace{0.1cm}(= A + B).$$

In der Literatur ist auch die Bezeichnung Summenmenge gebräuchlich und es wird manchmal das Pluszeichen benutzt. In unserem Tutorial verwenden wir jedoch ausschließlich das $∪$-Zeichen.

Anhand der Grafik sind die folgenden Gesetzmäßigkeiten der Mengenlehre leicht einzusehen: $$A \cup \it \phi = A \rm \hspace{3.6cm}(Vereinigung \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}leeren \hspace{0.15cm}Menge),$$ $$A\cup G = G \rm \hspace{3.6cm}(Vereinigung \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}Grundmenge),$$ $$A\cup A = A \hspace{3.6cm}(\rm Tautologiegesetz),$$ $$A\cup B = B\cup A \hspace{2.75cm}(\rm Kommutativgesetz),$$ $$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.55cm}(\rm Assoziativgesetz).$$

Ist über die Ereignismengen $A$ und $B$ nichts weiter bekannt, so können für die Wahrscheinlichkeit der Vereinigungsmenge nur eine untere und eine obere Schranke angegeben werden: $${\rm Max}({\rm Pr} (A), {\rm Pr} (B)) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$

• Die Wahrscheinlichkeit der Vereinigungsmenge ist gleich der unteren Schranke, wenn $A$ eine Teilmenge von $B$ ist oder umgekehrt.
• Die obere Schranke gilt für disjunkte Mengen.

Betrachtet man die beiden Ereignisse

• $A :=$ „die Augenzahl ist größer oder gleich 5” = {5, 6}   ⇒   ${\rm Pr} (A)= 2/6= 1/3$,
• $B :=$ „die Augenzahl ist geradzahlig” = {2, 4, 6}   ⇒   ${\rm Pr} (B)= 3/6= 1/2$,

so beinhaltet die Vereinigungsmenge vier Elemente: $(A \cup B) = \{2, 4, 5, 6 \}$   ⇒   ${\rm Pr} (A \cup B) = 4/6 = 2/3$.

• Die untere Schranke ergibt sich zu ${\rm Pr} (A \cup B) \ge {\rm Max}({\rm Pr} (A), {\rm Pr} (B)) = 3/6.$
• Für die obere Schranke gilt $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$

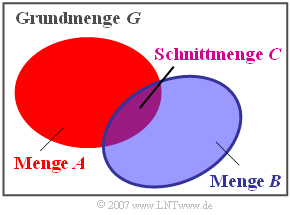
Schnittmenge

Eine weitere wichtige mengentheoretische Verknüpfung stellt die Schnittmenge dar.

Die Schnittmenge $C$ zweier Mengen $A$ und $B$ beinhaltet alle diejenigen Elemente, die sowohl in der Menge $A$ als auch in der Menge $B$ enthalten sind (englisch: Intersecting Set ). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: $$C = A \cap B \hspace{0.2cm}(= A \cdot B).$$

In der Literatur ist hierfür auch die Bezeichnung Produktmenge gebräuchlich und man verwendet das Multiplikationssymbol.

In der Grafik ist die Schnittmenge violett dargestellt. Analog zur Vereinigungsmenge sind hier folgende Gesetzmäßigkeiten zu nennen: $$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(Schnitt \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}leeren \hspace{0.15cm}Menge),$$ $$A \cap G = A \rm \hspace{3.6cm}(Schnitt \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}Grundmenge),$$ $$A\cap A = A \rm \hspace{3.6cm}(Tautologiegesetz),$$ $$A\cap B = B\cap A \rm \hspace{2.75cm}(Kommutativgesetz),$$ $$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.55cm}(Assoziativgesetz).$$

Ist über die Mengen $A$ und $B$ nichts weiter bekannt, so kann für die Wahrscheinlichkeit der Schnittmenge keine Aussage getroffen werden. Gilt jedoch ${\rm Pr} (A) \le 1/2$ und gleichzeitig ${\rm Pr} (B) \le 1/2$, so kann eine untere und eine obere Schranke angegeben werden: $0 \le {\rm Pr} (A ∩ B) \le {\rm Min}({\rm Pr} (A), {\rm Pr} (B)).$

${\rm Pr}(A ∩ B)$ wird manchmal auch „Verbundwahrscheinlichkeit” genannt und manchmal mit ${\rm Pr}(A, \ B)$ bezeichnet:

• ${\rm Pr}(A ∩ B)$ ist gleich der oberen Schranke, wenn $A$ eine Teilmenge von $B$ ist oder umgekehrt.
• Die untere Schranke ergibt sich für die Verbundwahrscheinlichkeit von disjunkten Mengen.

Wir betrachten wieder die beiden Ereignisse

• $A :=$ „die Augenzahl ist größer oder gleich 5” = {5, 6}   ⇒   ${\rm Pr} (A)= 2/6= 1/3$, und
• $B :=$ „die Augenzahl ist geradzahlig” = {2, 4, 6}   ⇒   ${\rm Pr} (B)= 3/6= 1/2$,

Die Schnittmenge beinhaltet nur ein einziges Element: $(A ∩ B) = \{ 6 \}$   ⇒   ${\rm Pr} (A ∩ B) = 1/6$.

• Die obere Schranke ergibt sich zu ${\rm Pr} (A ∩ B) \le {\rm Min}({\rm Pr} (A), {\rm Pr} (B)) = 2/6.$
• Die untere Schranke der Schnittmenge ist hier wegen ${\rm Pr} (A) \le 1/2$ und ${\rm Pr} (B) \le 1/2$ gleich $0$.

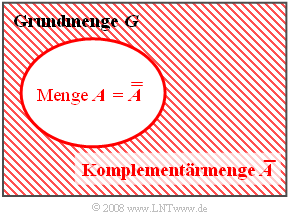
Komplementärmenge

Die Komplementärmenge (englisch: Complementary Set) von $A$ wird oft durch eine überstreichende Linie gekennzeichnet. Sie beinhaltet alle die Elemente, die in der Menge $A$ nicht enthalten sind, und es gilt für deren Wahrscheinlichkeit: $$\rm Pr(\overline{\it A}) = 1- Pr(\it A).$$

Im dargestellten Venndiagramm ist die zu $A$ komplementäre Menge schraffiert dargestellt. Aus diesem Schaubild sind einige mengentheoretische Beziehungen zu erkennen:

• Die Komplementärmenge der komplementären Menge von $A$ ist die Menge $A$ selbst:

$$\overline{\overline{A}} = A.$$

• Die Vereinigungsmenge einer Menge $A$ mit der Komplentärmenge ergibt die Grundmenge:

$$\rm Pr(\it A \cup \overline{\it A}) = \rm Pr(\it G) = \rm 1.$$

• Die Schnittmenge von $A$ mit der zugehörigen Komplementärmenge ergibt die leere Menge:

$$\rm Pr(\it A \cap \overline{\it A}) = \rm Pr(\it \phi) \rm = 0.$$

Ausgehend von der Menge

• $A :=$ „die Augenzahl ist kleiner als 5” = {1, 2, 3, 4}   ⇒   ${\rm Pr} (A)= 2/3$

lautet die zugehörige Komplentärmenge:

• $\overline{A} :=$ „die Augenzahl ist größer oder gleich 5” = {5, 6}   ⇒   ${\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$

Echte Teilmenge – unechte Teilmenge

Man bezeichnet $A$ als eine echte Teilmenge von $B$ und schreibt hierfür $A ⊂ B$, wenn alle Elemente von $A$ auch in $B$ enthalten sind, aber nicht gleichzeitig alle Elemente von $B$ auch in $A$ (englisch: Strict Subset). In diesem Fall gilt für die Wahrscheinlichkeiten: $$\rm Pr(\it A) < \rm Pr(\it B).$$

Diese mengentheoretische Relation wird durch das rechte Venndiagramm veranschaulicht.

Dagegen bezeichnet man $A$ als eine unechte Teilmenge von $B$ und verwendet die Notation $$A \subseteq B = (A \subset B) \cup (A = B),$$ wenn $A$ entweder eine echte Teilmenge von $B$ ist oder $A$ und $B$ gleiche Mengen sind.

Für die Wahrscheinlichkeiten gilt dann die Größenrelation ${\rm Pr} (A) \le {\rm Pr} (B)$. Das Gleichheitszeichen gilt nur für den Sonderfall identischer Mengen.

Es gelten aber auch die beiden als Absorptionsgesetze bekannten Gleichungen: $$(A \cap B) \cup A = A ,$$ $$(A \cup B) \cap A = A,$$

da die Schnittmenge $A ∩ B$ stets eine Teilmenge von $A$ ist, aber gleichzeitig auch $A$ eine Teilmenge der Vereinigungsmenge $A ∪ B$ ist.

Wir betrachten bei unserem Standardexperiment „Werfen eines Würfels”  ⇒  $G = ${1, 2, 3, 4, 5, 6 } nun die beiden Ereignisse

• $A :=$ „die Augenzahl ist ungerade” = {1, 3, 5}   ⇒   ${\rm Pr} (A)= 3/6$, und
• $B :=$ „die Augenzahl ist eine Primzahl” = {1, 2, 3, 5}   ⇒   ${\rm Pr} (B)= 4/6$.

Man erkennt, dass $A$ eine (echte) Teilmenge der Menge $B$ ist. Dementsprechend gilt auch $\rm Pr(\it A) < \rm Pr(\it B).$

Theoreme von de Morgan

Bei vielen Aufgaben aus der Mengenlehre sind die beiden Theoreme von de Morgan äußerst nützlich. Diese lauten: $$\overline{A \cup B} = \overline{A} \cap \overline{B},$$ $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$

Diese Gesetzmäßigkeiten sind im obigen Schaubild veranschaulicht:

• Die Menge $A$ ist rot dargestellt und die Menge $B$ blau.
• Die Komplentärmenge $\overline {A}$ von $A$   ist in horizontaler Richtung schraffiert.
• Die Komplentärmenge $\overline {B}$ von $B$ ist in vertikaler Richtung schraffiert.
• Das Komplement $\overline{A \cup B}$ der Vereinigungsmenge ${A \cup B}$ ist sowohl horizontal als auch vertikal schraffiert.
• Es ist damit gleich der Schnittmenge $\overline{A} \cap \overline{B}$ der beiden Komplentärmengen von $A$ und $B$:

$$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$

Auch die zweite Form des de Morgan-Theorems lässt sich mit diesem Venndiagramm grafisch verdeutlichen:

• Die Schnittmenge $A ∩ B$ (im Bild violett dargestellt) ist weder horizontal noch vertikal schraffiert.
• Das Komplement $\overline{A ∩ B}$der Schnittmenge ist dementsprechend entweder horizontal, vertikal oder in beiden Richtungen schraffiert.
• Nach dem zweiten Theorem von de Morgan ist das Komplement der Schnittmenge gleich der Vereinigungsmenge der beiden Komplentärmengen von $A$ und $B$:

$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$

Wir betrachten nun die beiden Mengen

• $A : =$ „die Augenzahl ist ungeradzahlig” = {1, 3, 5},
• $B : =$ „die Augenzahl ist größer als 2” = {3, 4, 5, 6}.

Daraus folgen die beiden komplementären Mengen

• $\overline {A} : =$ „die Augenzahl ist geradzahlig” = {2, 4, 6},
• $\overline {B} : =$ „die Augenzahl ist kleiner als 3” = {1, 2}.

Weiter erhält man mit den obigen Theoremen die folgenden Teilmengen: $$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\}\hspace{0.5 cm}\rm und \hspace{0.5cm} \overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$

Disjunkte Mengen

Zwei Mengen $A$ und $B$ nennt man disjunkt (englisch: disjoint) oder miteinander unvereinbar, wenn es kein einziges Element gibt, das sowohl in $A$ als auch in $B$ enthalten ist.

Das Schaubild zeigt zwei disjunkte Mengen $A$ und $B$ im Venndiagramm. In diesem Sonderfall gelten die folgenden Aussagen:

• Die Schnittmenge zweier disjunkter Mengen $A$ und $B$ ergibt stets die leere Menge:

$$\rm Pr(\it A \cap \it B) = \rm Pr(\it \phi) = \rm 0.$$

• Die Wahrscheinlichkeit der Vereinigungsmenge zweier disjunkter Mengen $A$ und $B$ ist immer gleich der Summe der beiden Einzelwahrscheinlichkeiten:

$${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$

Bei unserem Standardexperiment sind die beiden Mengen

• $A :=$ „die Augenzahl ist kleiner als 3” = {1, 2} ⇒ ${\rm Pr}( A) = 2/6$, und
• $B :=$ „die Augenzahl ist größer als 3” = {4, 5, 6} ⇒ ${\rm Pr}( B) = 3/6$

zueinander disjunkt, da $A$ und $B$ kein einziges gemeinsames Element beinhalten.

• Die Schnittmenge ergibt die leere Menge: ${A \cap B} = \phi$.
• Die Wahrscheinlichkeit der Vereinigungsmenge ${A \cup B} $ = {1, 2, 4, 5, 6} ist gleich ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$

Additionstheorem

Nur bei disjunkten Mengen $A$ und $B$ gilt für die Wahrscheinlichkeit der Vereinigungsmenge der Zusammenhang ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$ . Wie errechnet sich diese Wahrscheinlichkeit aber bei allgemeinen, nicht notwendigerweise disjunkten Ereignissen?

Betrachten Sie hierzu das folgende Venndiagramm mit der violett dargestellten Schnittmenge $A ∩ B$.

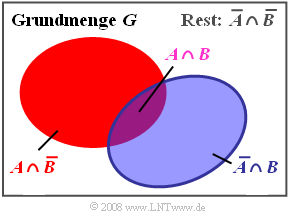
• Die rote Menge beinhaltet alle Elemente, die zu $A$ gehören, aber nicht zu $B$.
• Die Elemente von $B$, die nicht gleichzeitig in $A$ enthalten sind, erkennt man an der blauen Farbe.
• Alle roten, blauen und violetten Flächen zusammen ergeben die Vereinigungsmenge $A ∪ B$.

Aus dieser mengentheoretischen Darstellung erkennt man folgende Zusammenhänge: $${\rm Pr}(A) \hspace{0.75cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$ $${\rm Pr}(B) \hspace{0.75cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$ $${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) \rm + {\rm Pr}(\overline{A} \cap {B}).$$

Addiert man die ersten beiden Gleichungen und subtrahiert davon die dritte, so erhält man: $${\rm Pr}(A) \rm +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$

Durch Umstellen dieser Gleichung kommt man zum sogenannten Additionstheorem (englisch: Addition Rule) für zwei beliebige, nicht notwendigerweise disjunkte Ereignisse: $${\rm Pr}(A \cup B) =C + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$

Wir betrachten die beiden Mengen

• $A :=$ „die Augenzahl ist ungeradzahlig” = {1, 3, 5}   ⇒   ${\rm Pr}(A) = 3/6$, und
• $B :=$ „die Augenzahl ist größer 2” = {3, 4, 5, 6}   ⇒   ${\rm Pr}(B) = 4/6$.

Damit ergeben sich für die Wahrscheinlichkeiten

• der Vereinigungsmenge   ⇒   ${\rm Pr}((A ∪ B) = 5/6$, und
• der Schnittmenge   ⇒   ${\rm Pr}((A ∩ B) = 2/6$.

Die Zahlenwerte zeigen die Gültigkeit des Additionstheorems: $5/6 = 3/6 + 4/6 − 2/6$.

Vollständiges System

Im letzten Abschnitt zu diesem Kapitel betrachten wir wieder mehr als zwei mögliche Ereignisse, nämlich allgemein $I$. Diese Ereignisse werden im Folgenden mit $A_i$ bezeichnet, und es gilt für den Laufindex: $1 ≤ i ≤ I$ .

Eine Konstellation mit den Ereignissen $A_1, ... , A_i, ... , A_I$ bezeichnet man dann und nur dann als ein vollständiges System, wenn die beiden folgenden Bedingungen erfüllt sind:

• Alle Ereignisse sind paarweise disjunkt:

$$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$

• Die Vereinigung aller Ereignismengen ergibt die Grundmenge:

$$\bigcup_{i=1}^{I} A_i = G.$$

Aufgrund dieser beiden Voraussetzungen gilt dann für die Summe aller Wahrscheinlichkeiten: $$\rm \sum_{\it i \rm =1}^{ \it I} \rm Pr(\it A_i) = \rm 1.$$

Die Ereignismengen $A_1$ = {1, 5} und $A_2$ = {2, 3} ergeben beim Zufallsexperiment „Werfen eines Würfels” zusammen mit der Menge $A_3$ = {4, 6} ein vollständiges System, nicht jedoch beim Experiment „Werfen einer Roulettekugel”.

Ein Beispiel für ein vollständiges System ist auch eine diskrete Zufallsgröße $X$ = { $x_1, x_2, ... , x_I$} mit den Auftrittswahrscheinlichkeiten entsprechend der Wahrscheinlichkeitsfunktion: $$P_X(X) = \left [ \hspace{0.1cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}... \hspace{0.15cm}, P_X(x_I) \hspace{0.05cm} \right ] = \left [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}... \hspace{0.15cm}, p_I \hspace{0.05cm} \right ] \hspace{0.05cm}$$ $$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}... \hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$

Die möglichen Ergebnisse $x_i$ der Zufallsgröße $X$ sind paarweise zueinander disjunkt und die Summe aller Auftrittswahrscheinlichkeiten $p_1 + p_2 + ... + \hspace{0.05cm} p_I$ liefert grundsätzlich das Ergebnis 1.

Es gelte $X$= {0, 1, 2} und $P_X (X)$ = [0.2, 0.5, 0.3]. Dann gilt: $${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$

Bei der Zufallsgröße $X$ = {1, π, e} und gleichem $P_X(X)$ = [0.2, 0.5, 0.3] lauten die Zuordnungen: $${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$ Hinweis: Die Wahrscheinlichkeitsfunktion $P_X(X)$ macht lediglich Aussagen über die Wahrscheinlichkeiten, nicht jedoch über den Wertevorrat { $x_1, x_2, ... , x_I$} der Zufallsgröße $X$. Diese zusätzliche Information liefert die Wahrscheinlichkeitsdichtefunktion (WDF).