Aufgaben:Exercise 4.7: Weighted Sum and Difference

• Return to book

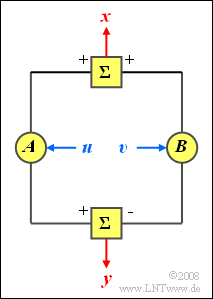
Die Zufallsgrößen $u$ und $v$ seien statistisch voneinander unabhängig, jeweils mit Mittelwert $m$ und Varianz $\sigma^2$. Beide Größen besitzen gleiche WDF und VTF. Über den Verlauf dieser Funktionen sei zunächst nichts bekannt.

Es werden nun zwei neue Zufallsgrößen $x$ und $y$ entsprechend den nachfolgenden Gleichungen gebildet:

$$x = A \cdot u + B \cdot v,$$

$$y= A \cdot u - B \cdot v.$$

Hierbei bezeichnen $A$ und $B$ (beliebige) konstante Werte.

• Für die Teilaufgaben (1) bis (4) gelte $m= 0$, $\sigma = 1$, $A = 1$ und $B = 2$.
• Bei der Teilaufgabe (6) wird vorausgesetzt, dass $u$ und $v$ jeweils gaußverteilt mit Mittelwert $m= 1$ und Streuung $\sigma = 0.5$ seien. Für die Konstanten gelte $A = B = 1$.
• Für die Aufgabe (7) gelte weiterhin $A = B = 1$. hier seien die Zufallsgrößen $u$ und $v$ symmetrisch zweipunktverteilt auf $\pm$1:

$${\rm Pr}(u=1) = {\rm Pr}(u=-1) = {\rm Pr}(v=1) = {\rm Pr}(v=-1) =0.5.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie groß sind Mittelwert und Streuung von $x$ für $A = 1$ und $B = 2$?

$m_x \ = $

$\sigma_x \ = $

2

Wie groß sind Mittelwert und Streuung von $y$ für $A = 1$ und $B = 2$?

$m_y \ = $

$\sigma_y \ = $

3

Berechnen Sie die Kovarianz $\mu_{xy}$. Welcher Wert ergibt sich für $A = 1$ und $B = 2$?

$\mu_{xy} \ = $

4

Berechnen Sie den Korrelationskoeffizienten $\rho_{xy}$ in Abhängigkeit des Quotienten $B/A$. Welcher Koeffizient ergibt sich für $A = 1$ und $B = 2$?

$\rho_{xy}\ = $

5

Welche der folgenden Aussagen gelten immer?

	Für $B = 0$ sind die Zufallsgrößen $x$ und $y$ streng korreliert.
	Es gilt $\rho_{xy}(-B/A) = -\rho_{xy}(B/A)$.
	Im Grenzfall $B/A \to \infty$ sind die Zufallsgrößen $x$ und $y$ streng korreliert.
	Für $A =B$ sind die Zufallsgrößen $x$ und $y$ unkorreliert.

6

Welche Aussagen sind zutreffend, wenn $A =B = 1$ gilt und $u$ und $v$ jeweils gaußverteilt sind mit Mittelwert $m = 1$ und Streuung $\sigma = 0.5$?

	Die Zufallsgrößen $x$ und $y$ sind unkorreliert.
	Die Zufallsgrößen $x$ und $y$ sind statistisch unabhängig.

7

Welche Aussagen treffen zu, wenn $u$ und $v$ symmetrisch zweipunktverteilt sind und $A =B = 1$ gilt?

	Die Zufallsgrößen $x$ und $y$ sind unkorreliert.
	Die Zufallsgrößen $x$ und $y$ sind statistisch unabhängig.

Musterlösung

Solution

(1)  Da die Zufallsgrößen $u$ und $v$ mittelwertfrei sind $(m = 0)$, ist auch die Zufallsgröße $x$ mittelwertfrei:

$$m_x = (A +B) \cdot m \hspace{0.15cm}\underline{ =0}.$$

Für die Varianz und die Streuung gelten:

$$\sigma_x^2 = (A^2 +B^2) \cdot \sigma^2 = 5; \hspace{0.5cm} \sigma_x = \sqrt{5}\hspace{0.15cm}\underline{ \approx 2.236}.$$

(2)  Da $u$ und $v$ die gleiche Streuung besitzen, gilt auch $\sigma_y =\sigma_x \hspace{0.15cm}\underline{ \approx 2.236}$. Wegen $m=0$ gilt zudem $m_y = m_x \hspace{0.15cm}\underline{ =0}.$ Bei mittelwertbehafteten Zufallsgrößen $u$ und $v$ ergäbe sich dagegen für $m_y = (A -B) \cdot m$ ein anderer Wert als für $m_x = (A +B) \cdot m$.

(3)  Wir gehen hier in der Musterlösung von dem allgemeineren Fall $m \ne 0$ aus. Dann gilt für das gemeinsame Moment:

$$m_{xy} = {\rm E} [x \cdot y ] = {\rm E} [(A \cdot u + B \cdot v) (A \cdot u - B \cdot v)] . $$

Nach den allgemeinen Rechenregeln für Erwartungswerte folgt daraus:

$$m_{xy} = A^2 \cdot {\rm E} [u^2 ] - B^2 \cdot {\rm E} [v^2 ] = (A^2 - B^2)(m^2 + \sigma^2).$$

Damit ergibt sich die Kovarianz zu

$$\mu_{xy} = m_{xy} - m_{x} \cdot m_{y}= (A^2 - B^2)(m^2 + \sigma^2) - (A + B)(A-B) \cdot m^2 = (A^2 - B^2) \cdot \sigma^2.$$

Mit $\sigma = 1$, $A = 1$ und $B = 2$ erhält man $\mu_{xy} \hspace{0.15cm}\underline{ =-3}$ und zwar unabhängig vom Mittelwert $m$ der Größen $u$ und $v$.

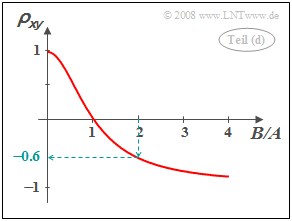
(4)  Der Korrelationskoeffizient ergibt sich zu

$$\rho_{xy} =\frac{\mu_{xy}}{\sigma_x \cdot \sigma_y} = \frac{(A^2 - B^2) \cdot \sigma^2}{(A^2 +B^2) \cdot \sigma^2} \hspace{0.5 cm}\Rightarrow \hspace{0.5 cm}\rho_{xy} =\frac{1 - (B/A)^2} {1 +(B/A)^2}.$$

Mit $B/A = 2$ folgt daraus $\rho_{xy} \hspace{0.15cm}\underline{ =-0.6}$.

(5)  Richtig sind die Aussagen 1, 3 und 4:

• Aus $B= 0$ folgt $\rho_{xy} = 1$ (strenge Korrelation). Man erkennt weiter, dass in diesem Fall $x = u$ und $y = u$ identische Zufallsgrößen sind.
• Die zweite Aussage ist nicht zutreffend: Für $A = 1$ und $B= -2$ ergibt sich ebenfalls $\rho_{xy} = -0.6$. Das Vorzeichen des Quotienten spielt also keine Rolle, weil in der in der Teilaufgabe (4) berechneten Gleichung der Quotient $B/A$ nur quadratisch auftritt.
• Ist $B \gg A$, so werden sowohl $x$ als auch $y$ fast ausschließlich durch die Zufallsgröße $v$ bestimmt und es ist $ y \approx -x$. Dies entspricht dem Korrelationskoeffizienten $\rho_{xy} = -1$.
• Dagegen ergibt sich für $B/A = 1$ stets der Korrelationskoeffizient $\rho_{xy} = 0$ und damit die Unkorreliertheit zwischen $x$ und $y$.

(6)  Beide Aussagen richtig sind richtig: Bei $A=B$ sind $x$ und $y$ stets (d. h. bei jeder beliebigen WDF der Größen $u$ und $v$) unkorreliert. Die neuen Zufallsgrößen $x$ und $y$ sind hier also ebenfalls gaußverteilt.

• Bei Gaußschen Zufallsgrößen folgt aber aus der Unkorreliertheit auch die statistische Unabhängigkeit und umgekehrt.

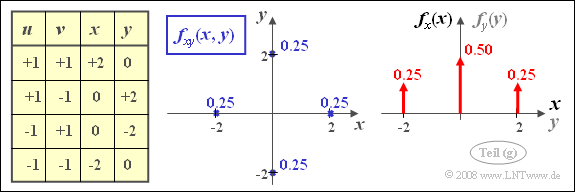
(7)  Hier ist nur die Aussage 1 zutreffend:

• Der Korrelationskoeffizient ergibt sich mit $A=B= 1$ auch hier zu $\rho_{xy} = 0$. Das heißt, dass $x$ und $y$ unkorreliert sind.
• Dagegen erkennt man aus der nachfolgend skizzierten 2D-WDF, dass die Bedingung der statistischen Unabhängigkeit im nun vorliegenden Fall nicht mehr gegeben ist. Vielmehr gilt: $f_{xy}(x, y) \ne f_{x}(x) \cdot f_{y}(y)$.