Difference between revisions of "Aufgaben:Exercise 4.09Z: Periodic ACF"
From LNTwww
m (Nabil verschob die Seite Zusatzaufgaben:4.09 Periodische AKF nach 4.09Z Periodische AKF) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID380__Sto_Z_4_9.png|right|]] | + | [[File:P_ID380__Sto_Z_4_9.png|right|Mehrstufiges Rechtecksignal]] |
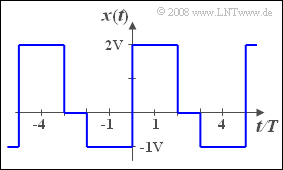
| − | + | Wir betrachten in dieser Aufgabe einen periodischen und gleichzeitig ergodischen stochastischen Prozess $\{x_i(t)\}$, der durch die dargestellte Musterfunktion $x(t)$ vollständig charakterisiert ist. | |
| − | + | Weitere Mustersignale des Zufallsprozesses $\{x_i(t)\}$ erhält man durch Verschiebung um unterschiedlich große Verzögerungen $\tau_i$, wobei $\tau_i$ als gleichverteilt zwischen $0$ und der Periodendauer $T_0$ angenommen wird. | |
| − | : | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 14: | Line 16: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ermitteln Sie die Periodendauer | + | {Ermitteln Sie die Periodendauer $T_0$, normiert auf die in der Skizze definierte Zeitdauer $T$. |
|type="{}"} | |type="{}"} | ||
| − | $T_0/T$ | + | $T_0/T \ =$ { 5 3% } |
| − | {Wie groß ist der Gleichsignalanteil (lineare Mittelwert) des Prozesses? | + | {Wie groß ist der Gleichsignalanteil (lineare Mittelwert) $m_x$ des beschriebenen Prozesses $\{x_i(t)\}$? |
|type="{}"} | |type="{}"} | ||
| − | $m_x$ | + | $m_x \ =$ { 0.4 3% } $\ \rm V$ |
| − | {Wie groß ist die (auf den Widerstand 1 | + | {Wie groß ist die (auf den Widerstand $1 \hspace{0.05cm} \rm \Omega$ bezogene) Prozessleistung? |
|type="{}"} | |type="{}"} | ||
| − | $P_x$ | + | $P_x \ =$ { 2 3% } $\ \rm V^2$ |
| − | {Berechnen Sie die AKF-Werte für | + | {Berechnen Sie die AKF-Werte für $\tau = T$ und $\tau = 2T$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varphi_x(\tau = T) \ =$ { 0.6 3% } $\ \rm V^2$ |
| − | $\ | + | $\varphi_x(\tau = 2T) \ =$ { -1.236--1.164 } $\ \rm V^2$ |
| − | {Skizzieren Sie den AKF-Verlauf unter Berücksichtigung von Symmetrieen. Welche Werte ergeben sich für | + | {Skizzieren Sie den AKF-Verlauf unter Berücksichtigung von Symmetrieen. Welche Werte ergeben sich für $\tau = 3T$ und $\tau = 4T$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varphi_x(\tau = 3T) \ =$ { -1.236--1.164 } $\ \rm V^2$ |
| − | $\ | + | $\varphi_x(\tau = 4T)\ =$ { 0.6 3% } $\ \rm V^2$ |
| − | {Berechnen Sie den Erwartungswert der AKF bezüglich aller | + | {Berechnen Sie den Erwartungswert der AKF bezüglich aller $\tau$-Werte. Interpretieren Sie das Ergebnis. |
|type="{}"} | |type="{}"} | ||
| − | $E[\phi_x(\tau)]$ | + | ${\rm E}[\phi_x(\tau)]\ =$ { 0.16 3% } $\ \rm V^2$ |
Revision as of 12:27, 24 March 2017
Wir betrachten in dieser Aufgabe einen periodischen und gleichzeitig ergodischen stochastischen Prozess $\{x_i(t)\}$, der durch die dargestellte Musterfunktion $x(t)$ vollständig charakterisiert ist.
Weitere Mustersignale des Zufallsprozesses $\{x_i(t)\}$ erhält man durch Verschiebung um unterschiedlich große Verzögerungen $\tau_i$, wobei $\tau_i$ als gleichverteilt zwischen $0$ und der Periodendauer $T_0$ angenommen wird.
Hinweise:
- Die Aufgabe gehört zum Kapitel Autokorrelationsfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- 1. Die Periodendauer beträgt T0 = 5T.
- 2. Aufgrund der Periodizität genügt die Mittelung über eine Periodendauer T0:
- $$m_x = \frac{1}{T_0} \cdot \int_0^{T_0} x(t) \hspace{0.1cm}\rm d \it t \\ = \rm \frac{1}{5 \it T} (\rm 2V \cdot 2 \it T - \rm 1V \cdot 2 \it T) \hspace{0.15cm}\underline{= \rm 0.4 \,V}.$$
- 3. In analoger Weise zu Aufgabe 2) erhält man für die mittlere Leistung:
- $$P_x = \rm \frac{2 \it T}{5 \it T} ((\rm 2V)^2 +(- \rm 1V)^2 )\hspace{0.15cm}\underline{ = \rm 2 \,V^2}.$$
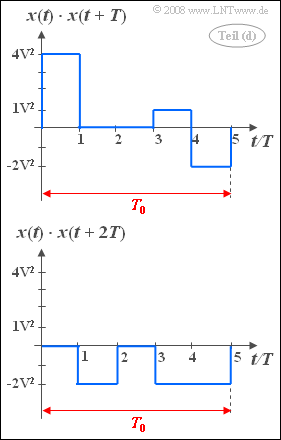
- 4. Die Bilder zeigen das Produkt x(t) · x(t + T) bzw. x(t) · x(t + 2T), jeweils im Bereich von 0 bis T0 = 5T.
- Zu beachten ist, dass x(t + T) eine Verschiebung des Signals x(t) um T nach links bedeutet. Aus den beiden Grafiken folgen die Beziehungen:
- $$\varphi_x (T)= \rm \frac{1}{5 } (\rm 4V^2 + \rm 1V^2 - \rm 2V^2) \hspace{0.15cm}\underline{= \rm 0.6\, V^2},$$
- $$\varphi_x (\rm 2\it T)= \rm \frac{1}{5 } (-\rm 2V^2 \cdot 3) \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2}.$$
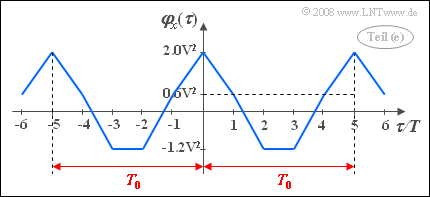
- 5. Eine Autokorrelationsfunktion ist stets gerade: φx(–τ) = φx(τ). Bei periodischen Prozessen ist die AKF zudem ebenfalls periodisch und zwar mit genau der gleichen Periodendauer T0 wie die einzelnen Musterfunktionen. Daraus folgt:
- $$\varphi_x (\rm 0) = \varphi_x (\rm 5\it T) = \varphi_x (\rm 10\it T) = .... = \it P_x = \rm 2 \,V^2,$$
- $$\varphi_x (\rm 3\it T) = \varphi_x (\rm -3\it T) =\varphi_x (\rm 2\it T) = .... \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2},$$
- $$\varphi_x (\rm 4\it T) = \varphi_x (\rm -4\it T) =\varphi_x (\rm \it T) = .... \hspace{0.15cm}\underline{= \rm 0.6 \,V^2}.$$
- Die berechneten AKF-Werte können durch Geradenabschnitte miteinander verbunden werden, da die Integration über Rechteckfunktionen stets lineare Teilabschnitte ergibt.
- 6. Die Mittelung über die 5 Intervalle 0 bis T, T bis 2T, ... , 4T bis 5T liefern (jeweils mit der Einheit V2): 1.3; –0.3, –1.2, –0.3, 1.3. Daraus ergibt sich der Erwartungswert E[φx(τ)] = 0.16 V2. Dies entspricht dem Quadrat des Mittelwertes mx (siehe Teilaufgabe 2).