Aufgaben:Exercise 4.15: PDF and Covariance Matrix

• Return to book

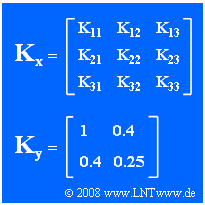
Wir betrachten hier die dreidimensionale Zufallsgröße $\mathbf{x}$, deren allgemein dargestellte Kovarianzmatrix $\mathbf{K}_{\mathbf{x}}$ in der Grafik angegeben ist. Die Zufallsgröße besitzt folgende Eigenschaften:

• Die drei Komponenten sind gaußverteilt und es gilt für die Elemente der Kovarianzmatrix:

$$K_{ij} = \sigma_i \cdot \sigma_j \cdot \rho_{ij}.$$

• Die Elemente auf der Hauptdiagonalen seien bekannt:

$$ K_{11} =1, K_{22} =0, K_{33} =0.25.$$

• Der Korrelationskoeffizient zwischen den Koeffizienten $x_1$ und $x_3$ beträgt $\rho_{13} = 0.8$.

Im zweiten Teil der Aufgabe soll die Zufallsgröße $\mathbf{y}$ mit den beiden Komponenten $y_1$ und $y_2$ betrachtet werden, deren Kovarianzmatrix $\mathbf{K}_{\mathbf{y}}$ durch die angegebenen Zahlenwerte $(1, 0.4, 0.25)$ bestimmt ist.

Die Wahrscheinlichkeitsdichtefunktion einer mittelwertfreien Gaußschen zweidimensionalen Zufallsgröße $\mathbf{y}$ lautet gemäß den Angaben auf der Seite Zusammenhang zwischen Kovarianzmatrix und WDF mit $N = 2$:

$$\mathbf{f_y}(\mathbf{y}) = \frac{1}{{(2 \pi) \cdot \sqrt{|\mathbf{K_y}|}}}\cdot {\rm exp}{\left(-\frac{1}{2}\cdot \mathbf{y} ^{\rm T}\cdot\mathbf{K_y}^{-1} \cdot \mathbf{y} \right)}= C \cdot {\rm exp}{\left(-\gamma_1 \cdot y_1^2 + \gamma_2 \cdot y_2^2 +\gamma_{12} \cdot y_1 \cdot y_2 \right)}.$$

In den Teilaufgaben (5) und (6) sollen der Vorfaktor $C$ und die weiteren WDF-Koeffizienten $\gamma_1$, $\gamma_2$ und $\gamma_{12}$ gemäß dieser Vektordarstellung berechnet werden. Dagegen würde die entsprechende Gleichung bei herkömmlicher Vorgehensweise entsprechend dem Kapitel Zweidimensionale Gaußsche Zufallsgrößen lauten:

$$f_{y_1,\hspace{0.1cm}y_2}(y_1,y_2)=\frac{\rm 1}{\rm 2\pi \sigma_1 \sigma_2 \sqrt{\rm 1-\rho^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1-\rho^{\rm 2})}\cdot(\frac { y_1^{\rm 2}}{\sigma_1^{\rm 2}}+\frac { y_2^{\rm 2}}{\sigma_2^{\rm 2}}-\rm 2\rho \frac{{\it y}_1{\it y}_2}{\sigma_1 \cdot \sigma_2}) \rm \Bigg].$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Verallgemeinerung auf N-dimensionale Zufallsgrößen.
• Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den Seiten Determinante einer Matrix sowie Inverse einer Matrix
• Bezug genommen wird auch auf das Kapitel Zweidimensionale Gaußsche Zufallsgrößen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Die Zufallsgröße $\mathbf{x}$ ist mit Sicherheit mittelwertfrei.
	Die Matrixelemente $K_{12}$, $K_{212}$, $K_{23}$ und $K_{32}$ sind $0$.
	Es gilt $K_{31} = -K_{13}$.

2

Berechnen Sie das Matrixelement der letzten Zeile und ersten Spalte.

$K_\text{31} \ = $

3

Berechnen Sie die Determinante $|\mathbf{K}_{\mathbf{y}}|$.

$|\mathbf{K}_{\mathbf{y}}| \ = $

4

Berechnen Sie die inverse Matrix $\mathbf{I}_{\mathbf{y}} = \mathbf{K}_{\mathbf{y}}^{-1}$ mit den Matrixelementen $I_{ij}$ :

$I_\text{11} \ = $

$I_\text{12} \ = $

$I_\text{21} \ = $

$I_\text{22} \ = $

5

Berechnen Sie den Vorfaktor $C$ der 2D-WDF. Vvergleichen Sie das Ergebnis mit der entsprechenden Formel gemäß dem Theorieteil.

$C\ = $

6

Bestimmen Sie die Koeffizienten im Argument der Exponentialfunktion. Vergleichen Sie das Ergebnis mit der 2D–WDF–Gleichung.

$\gamma_1 \ = $

$\gamma_2 \ = $

$\gamma_{12}\ = $

Musterlösung

Solution

(1)  Richtig ist nur der Lösungsvorschlag 2:

• Anhand der Kovarianzmatrix $\mathbf{K}_{\mathbf{x}}$ ist keine Aussage darüber möglich, ob die zugrunde liegende Zufallsgröße $\mathbf{x}$ mittelwertfrei oder mittelwertbehaftet ist, da ein eventueller Mittelwert $\mathbf{m}$ herausgerechnet wird.
• Um Aussagen über den Mittelwert machen zu können, müsste die Korrelationsmatrix $\mathbf{R}_{\mathbf{x}}$ bekannt sein.
• Aus $K_{22} = \sigma_2^2 = 0$ folgt zwingend, dass alle anderen Elemente in der zweiten Zeile $(K_{21}, K_{23})$ und der zweiten Spalte $(K_{12}, K_{32})$ ebenfalls $0$ sind.
• Dagegen ist die dritte Aussage falsch: Die Elemente sind symmetrisch zur Hauptdiagonalen, so dass stets $K_{31} = K_{13}$ gelten muss.

(2)  Aus $K_{11} = 1$ und $K_{33} = 0.25$ folgen direkt $\sigma_1 = 1$ und $\sigma_3 = 0.5$. Zusammen mit dem Korrelationskoeffizienten $\rho_{13} = 0.8$ (siehe Angabenblatt) erhält man somit:

$$K_{13} = K_{31} = \sigma_1 \cdot \sigma_2 \cdot \rho_{13}\hspace{0.15cm}\underline{= 0.4}.$$

(3)  Die Determinante der Matrix $\mathbf{K_y}$ lautet:

$$|{\mathbf{K_y}}| = 1 \cdot 0.25 - 0.4 \cdot 0.4 \hspace{0.15cm}\underline{= 0.09}.$$

(4)  Entsprechend den Angaben auf den Seiten „Determinante einer Matrix” und „Inverse einer Matrix” gilt:

$${\mathbf{I_y}} = {\mathbf{K_y}}^{-1} = \frac{1}{|{\mathbf{K_y}}|}\cdot \left[ \begin{array}{cc} 0.25 & -0.4 \\ -0.4 & 1 \end{array} \right].$$

Mit $|\mathbf{K_y}|= 0.09$ gilt deshalb weiter:

$$I_{11} = {25}/{9}\hspace{0.15cm}\underline{ = 2.777};\hspace{0.3cm} I_{12} = I_{21} = -40/9 \hspace{0.15cm}\underline{ = -4.447};\hspace{0.3cm}I_{22} = {100}/{9} \hspace{0.15cm}\underline{= 11.111}.$$

(5)  Ein Vergleich der Matrizen $\mathbf{K_y}$ und $\mathbf{K_x}$ unter der Nebenbedingung $K_{22} = 0$ zeigt, dass $\mathbf{x}$ und $\mathbf{y}$ identische Zufallsgrößen sind, wenn man $y_1 = x_1$ und $y_2 = x_3$ setzt. Somit gilt für die WDF-Parameter:

$$\sigma_1 =1, \hspace{0.3cm} \sigma_2 =0.5, \hspace{0.3cm} \rho = 0.8.$$

Der Vorfaktor entsprechend der allgemeinen WDF-Definition ist somit:

$$C =\frac{\rm 1}{\rm 2\pi \sigma_1 \sigma_2 \sqrt{\rm 1-\rho^2}}= \frac{\rm 1}{\rm 2\pi \cdot 1 \cdot 0.5 \cdot 0.6}= \frac{1}{0.6 \cdot \pi} \hspace{0.15cm}\underline{\approx 0.531}.$$

Mit der in der Teilaufgabe (3) berechneten Determinante ergibt sich das gleiche Ergebnis:

$$C =\frac{\rm 1}{\rm 2\pi \sqrt{|{\mathbf{K_y}}|}}= \frac{\rm 1}{\rm 2\pi \sqrt{0.09}} = \frac{1}{0.6 \cdot \pi}.$$

(6)  Die in der Teilaufgabe (4) berechnete inverse Matrix kann auch wie folgt geschrieben werden:

$${\mathbf{I_y}} = \frac{5}{9}\cdot \left[ \begin{array}{cc} 5 & -8 \\ -8 & 20 \end{array} \right].$$

Somit lautet das Argument $A$ der Exponentialfunktion:

$$A = \frac{5}{18}\cdot{\mathbf{y}}^{\rm T}\cdot \left[ \begin{array}{cc} 5 & -8 \\ -8 & 20 \end{array} \right]\cdot{\mathbf{y}} =\frac{5}{18}\left( 5 \cdot y_1^2 + 20 \cdot y_2^2 -16 \cdot y_1 \cdot y_2\right).$$

Durch Koeffizientenvergleich ergibt sich:

$$\gamma_1 = \frac{25}{18} \approx 1.389; \hspace{0.3cm} \gamma_2 = \frac{100}{18} \approx 5.556; \hspace{0.3cm} \gamma_{12} = - \frac{80}{18} \approx -4.444.$$

Entsprechend der herkömmlichen Vorgehensweise ergeben sich die gleichen Zahlenwerte:

$$\gamma_1 =\frac{\rm 1}{\rm 2\cdot \sigma_1^2 \cdot ({\rm 1-\rho^2})}= \frac{\rm 1}{\rm 2 \cdot 1 \cdot 0.36} \hspace{0.15cm}\underline{ \approx 1.389},$$

$$\gamma_2 =\frac{\rm 1}{\rm 2 \cdot\sigma_2^2 \cdot ({\rm 1-\rho^2})}= \frac{\rm 1}{\rm 2 \cdot 0.25 \cdot 0.36} = 4 \cdot \gamma_1 \hspace{0.15cm}\underline{\approx 5.556},$$

$$\gamma_{12} =-\frac{\rho}{ \sigma_1 \cdot \sigma_2 \cdot ({\rm 1-\rho^2})}= -\frac{\rm 0.8}{\rm 1 \cdot 0.5 \cdot 0.36} \hspace{0.15cm}\underline{ \approx -4.444}.$$