Difference between revisions of "Aufgaben:Exercise 4.6: AWGN Channel Capacity"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/AWGN–Kanalkapazität bei wertkontinuierlichem Eingang }} right| Wir gehen vom…“) |
|||
| Line 40: | Line 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {Welche Sendeleistung ist für <i>C</i> = 2 bit erforderlich? | ||
| + | |type="{}"} | ||
| + | $C = 2 bit: PX$ = { 15 3% } | ||
| + | |||
| + | {Unter welchen Voraussetzungen ist <i>I</i>(<i>X</i>; <i>Y</i>) = 2 bit überhaupt erreichbar? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | + <i>P<sub>X</sub></i> ist wie unter (a) ermittelt oder größer. |
| − | + | + Die Zufallsgröße <i>X</i> ist gaußverteilt. | |
| + | + Die Zufallsgröße <i>X</i> ist mittelwertfrei. | ||
| + | + Die Zufallsgrößen <i>X</i> und <i>N</i> sind unkorreliert. | ||
| + | - Die Zufallsgrößen <i>X</i> und <i>Y</i> sind unkorreliert. | ||
| + | |||
| + | |||
| + | |||
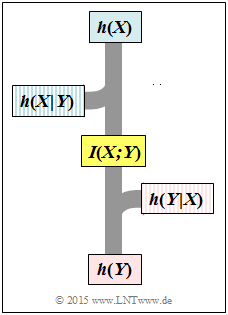
| + | {Berechnen Sie die differentiellen Entropien der Zufallsgrößen <i>N</i>, <i>X</i> und <i>Y</i> bei geeigneter Normierung, zum Beispiel <i>P<sub>N</sub></i> = 1 mW ⇒ <i>P′<sub>N</sub></i> = 1. | ||
| + | |type="{}"} | ||
| + | $h(N)$ = { 2.047 3% } | ||
| + | $h(X)$ = { 4 3% } | ||
| + | $h(Y)$ = { 4.047 3% } | ||
| − | { | + | {Wie lauten die weiteren informationstheoretischen Beschreibungsgrößen? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $h(Y|X)$ = { 2.047 3% } |
| + | $h(X|Y)$ = { 2 3% } | ||
| + | $h(XY)$ = { 6.047 3% } | ||
| + | |||
| + | |||
| + | {Welche Größen ergäben sich bei gleichem <i>P<sub>X</sub></i> im Grenzfall <i>P′<sub>N</sub></i> → 0? | ||
| + | |type="{}"} | ||
| + | $h(X)$ = { 4 3% } | ||
| + | $h(Y)$ = { 4 3% } | ||
| + | $h(Y|X)$ = { 0 3% } | ||
| + | $h(X|Y)$ = { 0 3% } | ||
| + | $I(X;Y)$ = { 4 3% } | ||
Revision as of 17:02, 4 April 2017
Wir gehen vom AWGN-Kanalmodell aus:
- X kennzeichnet den Eingang (Sender).
- N steht für eine gaußverteilte Störung.
- Y = X + N beschreibt den Ausgang (Empfänger) bei additiver Störung.
Für die Wahrscheinlichkeitsdichtefunktion der Störung gelte: $$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm exp}\left [ - \hspace{0.05cm}\frac{n^2}{2 \sigma_N^2} \right ] \hspace{0.05cm}.$$ Da die Zufallsgröße N mittelwertfrei ist ⇒ mN = 0, kann man die Varianz σN2 mit der Leistung PN gleichsetzen. In diesem Fall ist die differentielle Entropie der Zufallsgröße N wie folgt angebbar (mit Pseudo–Einheit „bit”): $$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$ In dieser Aufgabe wird PN = 1 mW vorgegeben. Dabei ist zu beachten:
- Die Leistung PN in obiger Gleichung muss wie die Varianz σN2 dimensionslos sein.
- Um mit dieser Gleichung arbeiten zu können, muss die physikalische Größe PN geeignet normiert werden, zum Beispiel entsprechend PN = 1 mW ⇒ P'N = 1.
- Bei anderer Normierung, beispielsweise PN = 1 mW ⇒ P'N = 0.001 ergäbe sich für h(N) ein völlig anderer Zahlenwert.
Weiter können Sie bei der Lösung dieser Aufgabe berücksichtigen:
- Die Kanalkapazität ist definiert als die maximale Transinformation zwischen Eingang X und Ausgang Y bei bestmöglicher Eingangsverteilung:
$$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) \hspace{0.05cm}.$$
- Die Kanalkapazität des AWGN–Kanals lautet:
$$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P\hspace{0.05cm}'_{\hspace{-0.05cm}X}}{P\hspace{0.05cm}'_{\hspace{-0.05cm}N}} \right )\hspace{0.05cm}.$$ Daraus ist ersichtlich, dass die die Kanalkapazität C und auch die Transinformation I(X; Y) im Gegensatz zu den differentiellen Entropien unabhängig von obiger Normierung ist.
- Bei gaußförmiger Stör–WDF fN(n) führt eine ebenfalls gaußförmige Eingangs–WDF fX(x) zur maximalen Transinformation und damit zur Kanalkapazität.
Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.2.
Fragebogen
Musterlösung