Aufgaben:Exercise 4.6: AWGN Channel Capacity

• Return to book

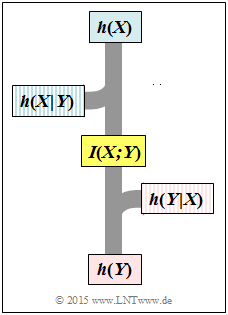
Wir gehen vom AWGN-Kanalmodell aus:

• X kennzeichnet den Eingang (Sender).
• N steht für eine gaußverteilte Störung.
• Y = X + N beschreibt den Ausgang (Empfänger) bei additiver Störung.

Für die Wahrscheinlichkeitsdichtefunktion der Störung gelte: $$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm exp}\left [ - \hspace{0.05cm}\frac{n^2}{2 \sigma_N^2} \right ] \hspace{0.05cm}.$$ Da die Zufallsgröße N mittelwertfrei ist  ⇒  m_N = 0, kann man die Varianz σ_N² mit der Leistung P_N gleichsetzen. In diesem Fall ist die differentielle Entropie der Zufallsgröße N wie folgt angebbar (mit Pseudo–Einheit „bit”): $$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$ In dieser Aufgabe wird P_N = 1 mW vorgegeben. Dabei ist zu beachten:

• Die Leistung P_N in obiger Gleichung muss wie die Varianz σ_N² dimensionslos sein.

• Um mit dieser Gleichung arbeiten zu können, muss die physikalische Größe P_N geeignet normiert werden, zum Beispiel entsprechend P_N = 1 mW  ⇒  P'_N = 1.

• Bei anderer Normierung, beispielsweise P_N = 1 mW  ⇒  P'_N = 0.001 ergäbe sich für h(N) ein völlig anderer Zahlenwert.

Weiter können Sie bei der Lösung dieser Aufgabe berücksichtigen:

• Die Kanalkapazität ist definiert als die maximale Transinformation zwischen Eingang X und Ausgang Y bei bestmöglicher Eingangsverteilung:

$$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) \hspace{0.05cm}.$$

• Die Kanalkapazität des AWGN–Kanals lautet:

$$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P\hspace{0.05cm}'_{\hspace{-0.05cm}X}}{P\hspace{0.05cm}'_{\hspace{-0.05cm}N}} \right )\hspace{0.05cm}.$$ Daraus ist ersichtlich, dass die die Kanalkapazität C und auch die Transinformation I(X; Y) im Gegensatz zu den differentiellen Entropien unabhängig von obiger Normierung ist.

• Bei gaußförmiger Stör–WDF f_N(n) führt eine ebenfalls gaußförmige Eingangs–WDF f_X(x) zur maximalen Transinformation und damit zur Kanalkapazität.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.2.

Fragebogen

1

Welche Sendeleistung ist für C = 2 bit erforderlich?

$C = 2 bit: PX$ =

2

Unter welchen Voraussetzungen ist I(X; Y) = 2 bit überhaupt erreichbar?

	PX ist wie unter (a) ermittelt oder größer.
	Die Zufallsgröße X ist gaußverteilt.
	Die Zufallsgröße X ist mittelwertfrei.
	Die Zufallsgrößen X und N sind unkorreliert.
	Die Zufallsgrößen X und Y sind unkorreliert.

3

Berechnen Sie die differentiellen Entropien der Zufallsgrößen N, X und Y bei geeigneter Normierung, zum Beispiel P_N = 1 mW  ⇒  P′_N = 1.

$h(N)$ =

$h(X)$ =

$h(Y)$ =

4

Wie lauten die weiteren informationstheoretischen Beschreibungsgrößen?

$h(Y|X)$ =

$h(X|Y)$ =

$h(XY)$ =

5

Welche Größen ergäben sich bei gleichem P_X  im Grenzfall P′_N  →  0?

$h(X)$ =

$h(Y)$ =

$h(Y|X)$ =

$h(X|Y)$ =

$I(X;Y)$ =

Musterlösung

Solution

a)  Die Gleichung für die AWGN–Kanalkapazität in „bit” lautet: $$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right )\hspace{0.05cm}.$$ Mit C_bit = 2 ergibt sich daraus: $$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + \frac{P_X}{P_N} \stackrel {!}{=} 2^4 = 16 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_X = 15 \cdot P_N \hspace{0.15cm}\underline{= 15\,{\rm mW}} \hspace{0.05cm}. $$ b)  Richtig sind die Lösungsvorschläge 1 bis 4. Begründung:

• Für P_X < 15 mW wird die Transinformation I(X; Y) stets kleiner als 2 bit sein, unabhängig von allen anderen Gegebenheiten.
• Mit P_X = 15 mW ist die maximale Transinformation I(X; Y) = 2 bit nur erreichbar, wenn die Eingangsgröße X gaußverteilt ist. Die Ausgangsgröße Y ist dann ebenfalls gaußverteilt.
• Weist die Zufallsgröße X einen Gleichanteil m_X auf, so ist die Varianz σ_X² = P_X – m_X² bei gegebenem P_X  kleiner, und es gilt I(X;Y) = 1/2 · log₂ (1 + σ_X²/P_N) < 2 bit.
• Voraussetzung für die gegebene Kanalkapazitätsgleichung ist, dass X und N unkorreliert sind. Wären dagegen die Zufallsgrößen X und Y unkorreliert, so ergäbe sich I(X; Y) = 0.

c)  Die angegebene Gleichung für die differentielle Entropie macht nur bei dimensionsloser Leistung Sinn. Mit der vorgeschlagenen Normierung erhält man:

• P_N = 1 mW  ⇒  P'_N = 1:

$$h(N) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 1 \right ) $$ $$ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 17.08 \right ) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm},$$

• P_X = 15 mW  ⇒  P′_X = 15:

$$h(X) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 15 \right ) $$ $$ = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \right ) + {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left (15 \right ) $$ $$ = \ 2.047\,{\rm bit} + 1.953\,{\rm bit} \hspace{0.15cm}\underline{= 4.000\,{\rm bit}}\hspace{0.05cm}, $$

• P_Y = P_X + P_N = 16 mW  ⇒  P′_Y = 16:

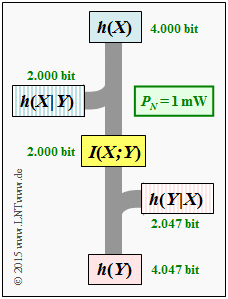
$$h(Y) = 2.047\,{\rm bit} + 2.000\,{\rm bit} \hspace{0.15cm}\underline{= 4.047\,{\rm bit}}\hspace{0.05cm}.$$ d)  Für die differentielle Irrelevanz gilt beim AWGN–Kanal: $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(N) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$ Entsprechend nebenstehender Grafik gilt aber auch: $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}. $$ Entsprechend kann die differentielle Äquivokation wie folgt berechnet werden: $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = 4.000 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.000\,{\rm bit}}\hspace{0.05cm}.$$ Abschließend wird auch noch die differentielle Verbundentropie angegeben, die aus obigem Schaubild nicht direkt ablesbar ist: $$h(XY) = h(X) + h(Y) - I(X;Y) = 4.000 \,{\rm bit} + 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 6.047\,{\rm bit}}\hspace{0.05cm}.$$

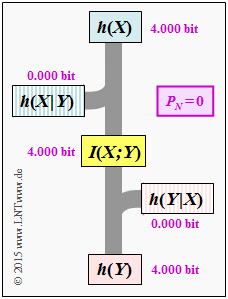
e)  Bei einem idealen Kanal erhält man mit h(X) = 4 bit: $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) \ = \ h(N) \hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm},$$ $$ h(Y) \ = \ h(X) \hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ I(X;Y) \ = \ h(Y) - h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)\hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) \ = \ h(X) - I(X;Y)\hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm}.$$ Die Grafik zeigt diese Größen in einem Flussdiagramm.

Das gleiche Diagramm ergäbe sich auch im wertdiskreten Fall mit M = 16 gleichwahrscheinlichen Symbolen  ⇒  H(X) = 4 bit. Man müsste nur jedes „h” durch ein „H” ersetzen.

x