Difference between revisions of "Aufgaben:Exercise 4.1Z: Calculation of Moments"
m (Guenter verschob die Seite 4.01Z Momentenberechnung nach 4.1Z Momentenberechnung) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2863__Inf_Z_4_1.png|right|]] | + | [[File:P_ID2863__Inf_Z_4_1.png|right|Exponential– und Laplaceverteilung]] |
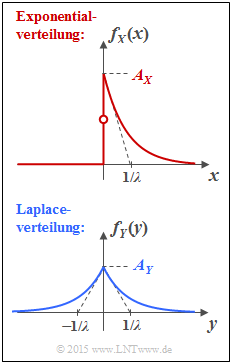
| − | Die Grafik zeigt oben die Wahrscheinlichkeitsdichtefunktion (WDF) der | + | Die Grafik zeigt oben die Wahrscheinlichkeitsdichtefunktion (WDF) der [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen|Exponentialverteilung]]: |
| − | $$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm exp}(-\lambda \cdot x) \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$ | + | :$$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm exp}(-\lambda \cdot x) \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$ |
| − | Darunter gezeichnet ist die WDF der | + | Darunter gezeichnet ist die WDF der [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen#Zweiseitige_Exponentialverteilung_.E2.80.93_Laplaceverteilung|Laplaceverteilung]], die für alle $y$–Werte wie folgt angegeben werden kann: |
| − | $$f_Y(y) = A_{ Y} \cdot {\rm exp}(-\lambda \cdot |y|)\hspace{0.05cm}.$$ | + | :$$f_Y(y) = A_{ Y} \cdot {\rm exp}(-\lambda \cdot |y|)\hspace{0.05cm}.$$ |
| − | Die zwei wertkontinuierlichen Zufallsgrößen | + | |
| − | + | Die zwei wertkontinuierlichen Zufallsgrößen $X$ und $Y$ sollen hinsichtlich der folgenden Kenngrößen verglichen werden: | |
| − | + | *dem linearen Mittelwert $m_1$ (Moment erster Ordnung), | |
| − | + | *dem Moment zweiter Ordnung ⇒ $m_2$, | |
| − | + | *der Varianz $\sigma^2 = m_2 - m_1^2$ ⇒ Satz von Steiner, | |
| − | + | *der Streuung $\sigma$. | |
| − | $$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$ | + | |
| − | $$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot | + | |
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Differentielle_Entropie|Differentielle Entropie]]. | ||
| + | *Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im Kapitel „Kontinuierliche Zufallsgrößen” des Buches [[Stochastische Signaltheorie]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Gegeben sind außerdem die beiden unbestimmten Integrale: | ||
| + | :$$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$ | ||
| + | :$$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot | ||
(\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) | (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist der Maximalwert | + | {Wie groß ist der Maximalwert $A_X$ der WDF$f_X(x)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $A_X = \lambda/2$, |
| − | + | + | + $A_X = \lambda$, |
| − | - | + | - $A_X = 1/\lambda$. |
| − | {Wie groß ist der Maximalwert | + | {Wie groß ist der Maximalwert $A_Y$ der WDF$f_Y(y)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $A_Y = \lambda/2$, |
| − | - | + | - $A_Y = \lambda$, |
| − | - | + | - $A_Y = 1/\lambda$. |
| − | {Gibt es ein Argument | + | {Gibt es ein Argument $z$, so dass $f_X(z) = f_Y(z)$ gilt? |
|type="[]"} | |type="[]"} | ||
+ Ja. | + Ja. | ||
| Line 42: | Line 51: | ||
{Welche Aussagen gelten für die Kenngrößen der Exponentialverteilung? | {Welche Aussagen gelten für die Kenngrößen der Exponentialverteilung? | ||
|type="[]"} | |type="[]"} | ||
| − | + Der lineare Mittelwert ist | + | + Der lineare Mittelwert ist $m_1 = 1/\lambda$. |
| − | + Der quadratische Mittelwert ist | + | + Der quadratische Mittelwert ist $m_2 = 2/\lambda^2$. |
| − | + Die Varianz ist | + | + Die Varianz ist $\sigma^2 = 1/\lambda^2$. |
{Welche Aussagen gelten für die Kenngrößen der Laplaceverteilung? | {Welche Aussagen gelten für die Kenngrößen der Laplaceverteilung? | ||
|type="[]"} | |type="[]"} | ||
| − | - Der lineare Mittelwert ist | + | - Der lineare Mittelwert ist $m_1 = 1/\lambda$. |
| − | + Der quadratische Mittelwert ist | + | + Der quadratische Mittelwert ist $m_2 = 2/\lambda^2$. |
| − | - Die Varianz ist | + | - Die Varianz ist $\sigma^2 = 1/\lambda^2$. |
| − | {Mit welcher Wahrscheinlichkeiten unterscheidet sich die Zufallsgröße | + | {Mit welcher Wahrscheinlichkeiten unterscheidet sich die Zufallsgröße ($X$ bzw. $Y$) vom Mittelwert $m$ betragsmäßig um mehr als die Streuung $\sigma$? |
|type="{}"} | |type="{}"} | ||
$Exponential: Pr(|X – mX| > σX)$ = { 0.135 3% } | $Exponential: Pr(|X – mX| > σX)$ = { 0.135 3% } | ||
Revision as of 17:04, 5 April 2017
Die Grafik zeigt oben die Wahrscheinlichkeitsdichtefunktion (WDF) der Exponentialverteilung:
- $$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm exp}(-\lambda \cdot x) \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$
Darunter gezeichnet ist die WDF der Laplaceverteilung, die für alle $y$–Werte wie folgt angegeben werden kann:
- $$f_Y(y) = A_{ Y} \cdot {\rm exp}(-\lambda \cdot |y|)\hspace{0.05cm}.$$
Die zwei wertkontinuierlichen Zufallsgrößen $X$ und $Y$ sollen hinsichtlich der folgenden Kenngrößen verglichen werden:
- dem linearen Mittelwert $m_1$ (Moment erster Ordnung),
- dem Moment zweiter Ordnung ⇒ $m_2$,
- der Varianz $\sigma^2 = m_2 - m_1^2$ ⇒ Satz von Steiner,
- der Streuung $\sigma$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im Kapitel „Kontinuierliche Zufallsgrößen” des Buches Stochastische Signaltheorie.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Gegeben sind außerdem die beiden unbestimmten Integrale:
- $$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$
- $$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \hspace{0.05cm}. $$
Fragebogen
Musterlösung
b) Aus der Grafik auf der Angabenseite erkennt man, dass die Höhe AY der Laplaceverteilung nur halb so groß ist wie das Maximum der Exponentialverteilung ⇒AY = λ/2 ⇒ Lösungsvorschlag 1.
c) Richtig ist JA, obwohl für z ≠ 0 stets fX(z) ≠ fY(z) gilt. Betrachten wir nun den Sonderfall z = 0:
- Für die Laplaceverteilung gilt fY(0) = λ/2.
- Bei der Exponentialverteilung unterscheiden sich der links- und der rechtsseitige Grenzwert für x → 0. Der WDF–Wert an der Stelle x = 0 ist der Mittelwert dieser beiden Grenzwerte:
$$f_X(0) = \frac{1}{2} \cdot [ 0 + \lambda] = \lambda/2 = f_Y(0)\hspace{0.05cm}.$$
d) Bei der Exponentialverteilung erhält man entsprechend [BS01] für
- den linearen Mittelwert (Moment erster Ordnung):
$$m_1 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot \left [\frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\right ]_{0}^{\infty}= {1}/{\lambda} \hspace{0.05cm},$$
- den quadratischen Mittelwert (Moment zweiter Ordnung):
$$m_2 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \right ]_{0}^{\infty} ={2}/{\lambda^2} \hspace{0.05cm}.$$ Daraus ergibt sich mit dem Satz von Steiner für die Varianz der Exponentialverteilung: $$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} -{1}/{\lambda^2} = {1}/{\lambda^2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \sigma = {1}/{\lambda}\hspace{0.05cm}.$$ Richtig sind also alle Lösungsvorschläge. Hinweis: Bei der Exponentialverteilung berechnet sich das Moment k–ter Ordnung allgemein zu mk = k!/λk ⇒ m1 = 1/λ, m2 = 2/λ2, m3 = 6/λ3, ...
e) Richtig ist nur der Lösungsvorschlag 2: Der quadratische Mittelwert der Laplaceverteilung ist aufgrund der symmetrischen WDF genau so groß wie bei der Exponentialverteilung: $$m_2 = \frac{\lambda}{2} \cdot \int_{-\infty}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.1cm}{\rm d}y = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y = {2}/{\lambda^2} \hspace{0.05cm}.$$ Der Mittelwert der Laplaceverteilung ist m1 = 0. Damit ist die Varianz der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung: $$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} - 0 ={2}/{\lambda^2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \sigma = {\sqrt{2}}/{\lambda}\hspace{0.05cm}.$$
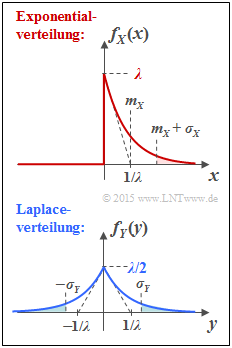
f) Für die Exponentialverteilung ergibt sich entsprechend der oberen Grafik mit mX = σX = 1/λ: $${\rm Pr}( |X - m_X| > \sigma_X) = {\rm Pr}( X > 2/\lambda) $$ $$\ = \lambda \cdot\int_{2/\lambda}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = -\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \right ]_{2/\lambda}^{\infty}$$ $$\ = {\rm e}^{-2} \hspace{0.15cm}\underline {\approx 0.135}\hspace{0.05cm}.$$ Für die Laplaceverteilung (untere Grafik) erhält man mit mY = 0 und σY = 20.5/λ: $${\rm Pr}( |Y - m_Y| > \sigma_Y) = 2 \cdot {\rm Pr}( Y > \sqrt{2}/\lambda) $$ $$\ = 2 \cdot \frac{\lambda}{2} \cdot\int_{\sqrt{2}/\lambda}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \right ]_{\sqrt{2}/\lambda}^{\infty}$$ $$\ = - {\rm e}^{-\sqrt{2}} \hspace{0.15cm}\underline {\approx 0.243}\hspace{0.05cm}.$$
Ein Vergleich der schraffierten Flächen in nebenstehender Grafik bestätigt das Ergebnis qualitativ: Die blauen Flächen sind zusammen etwas größer als die rote Fläche.