Difference between revisions of "Aufgaben:Exercise 5.4: Sine Wave Generator"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Digitale Filter }} right| :Die Grafik zeigt ein digitales Filter zweiter…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
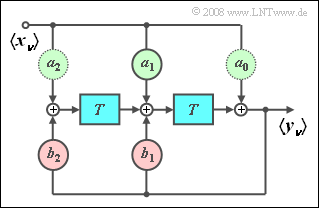
| − | [[File:P_ID622__Sto_A_5_4.png|right|]] | + | [[File:P_ID622__Sto_A_5_4.png|right|Realisierung eines Sinusgenerators]] |
| − | + | Die Grafik zeigt ein digitales Filter zweiter Ordnung, das zum Beispiel zur Erzeugung einer zeitdiskreten Sinusfunktion auf einem digitalen Signalprozessor (DSP) geeignet ist: | |
:$$\left\langle {y_\nu } \right\rangle = \left\langle {\, \sin ( {\nu T \omega _0 } )\, }\right\rangle .$$ | :$$\left\langle {y_\nu } \right\rangle = \left\langle {\, \sin ( {\nu T \omega _0 } )\, }\right\rangle .$$ | ||
| − | + | *Vorausgesetzt wird, dass die Eingangsfolge $\left\langle {x_\nu } \right\rangle$ eine (zeitdiskrete) Diracfunktion beschreibt. Damit sind gleichzeitig alle Ausgangswerte $y_\nu$ für Zeiten $\nu\lt 0$ identisch Null. | |
| − | + | *Die insgesamt fünf Filterkoeffizienten ergeben sich aus der [https://de.wikipedia.org/wiki/Z-Transformation <i>z</i>-Transformation]: | |
| − | |||
| − | |||
:$$z \{ {\sin ( {\nu T \omega _0 } )} \} = \frac{{z \cdot \sin \left( {\omega _0 T} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 T} \right) + 1}}.$$ | :$$z \{ {\sin ( {\nu T \omega _0 } )} \} = \frac{{z \cdot \sin \left( {\omega _0 T} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 T} \right) + 1}}.$$ | ||
| − | + | *Setzt man diese Gleichung durch ein rekursives Filter zweiter Ordnung $(M = 2)$ um, so erhält man die folgenden Filterkoeffizienten: | |
| − | |||
:$$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0,\\b_1 = 2 \cdot \cos \left( {\omega _0 T} \right),\quad b_2 = - 1.$$ | :$$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0,\\b_1 = 2 \cdot \cos \left( {\omega _0 T} \right),\quad b_2 = - 1.$$ | ||
| − | + | Im Bild ist bereits durch die hellere Umrandung markiert, dass auf die Filterkoeffizienten $a_0$ und $a_2$ verzichtet werden kann. | |
| − | : | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Digitale_Filter|Digitale Filter]] im vorliegenden Buch. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Für die Teilaufgaben (1) bis (3) gelte: | ||
:$$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$ | :$$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$ | ||
Revision as of 12:14, 19 April 2017
Die Grafik zeigt ein digitales Filter zweiter Ordnung, das zum Beispiel zur Erzeugung einer zeitdiskreten Sinusfunktion auf einem digitalen Signalprozessor (DSP) geeignet ist:
- $$\left\langle {y_\nu } \right\rangle = \left\langle {\, \sin ( {\nu T \omega _0 } )\, }\right\rangle .$$
- Vorausgesetzt wird, dass die Eingangsfolge $\left\langle {x_\nu } \right\rangle$ eine (zeitdiskrete) Diracfunktion beschreibt. Damit sind gleichzeitig alle Ausgangswerte $y_\nu$ für Zeiten $\nu\lt 0$ identisch Null.
- Die insgesamt fünf Filterkoeffizienten ergeben sich aus der z-Transformation:
- $$z \{ {\sin ( {\nu T \omega _0 } )} \} = \frac{{z \cdot \sin \left( {\omega _0 T} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 T} \right) + 1}}.$$
- Setzt man diese Gleichung durch ein rekursives Filter zweiter Ordnung $(M = 2)$ um, so erhält man die folgenden Filterkoeffizienten:
- $$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0,\\b_1 = 2 \cdot \cos \left( {\omega _0 T} \right),\quad b_2 = - 1.$$
Im Bild ist bereits durch die hellere Umrandung markiert, dass auf die Filterkoeffizienten $a_0$ und $a_2$ verzichtet werden kann.
Hinweise:
- Die Aufgabe gehört zum Kapitel Digitale Filter im vorliegenden Buch.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Für die Teilaufgaben (1) bis (3) gelte:
- $$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$
Fragebogen
Musterlösung
- 1. Die „1” am Eingang wirkt sich am Ausgang erst zum Zeitpunkt ν = 1 aus (wegen a0 = 0):
- $$y_0 \hspace{0.15cm} \underline{= 0},\quad y_1 \hspace{0.15cm} \underline{ = 0.5}.$$
- Bei ν = 2 wird auch der rekursive Teil des Filters wirksam:
- $$y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \hspace{0.15cm} \underline{ \approx 0.866}.$$
- 2. Für ν ≥ 2 ist das Filter rein rekursiv:
- $$y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2} .$$
- Insbesondere erhält man
- $$y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1;$$
- $$y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$$
- $$y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = {1}/{2};$$
- $$y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$$
- $$y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} \hspace{0.15cm} \underline{= - {1}/{2}}.$$
- 3. Durch Fortsetzung des rekursiven Algorithmuses aus (b) erhält man für große ν-Werte:
- $$y_\nu = y_{\nu - 12} .$$
- Daraus folgt T0/T = 12. Zum gleichen Ergebnis kommt man durch folgende Überlegungen:
- $$a_1 = \sin \left( {\omega _0 \cdot T} \right) = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right)\mathop = \limits^! {1}/{2} = \sin \left( {{{\rm{\pi }}}/{6}} \right).$$
- $${\rm \Rightarrow} \;\;{2T}/{T_0 } = {1}/{6}\quad \Rightarrow \;\;{T_0 }/{T} = 12.$$
- Die Überprüfung des Koeffizienten b1 bestätigt die Rechnung:
- $$b_1 = 2 \cdot \cos \left( {{{\rm{\pi }}}/{6}} \right) = 2 \cdot c{\sqrt 3 }/{2} = \sqrt 3 .$$
- 4. Aus f0 = 10 kHz folgt T0 = 100 μs bzw. T0/T = 100. Damit ergibt sich:
- $$a_1 = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = \sin \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 0.062},$$
- $$b_1 = 2 \cdot \cos \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = 2 \cdot \cos \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 1.996}.$$