Difference between revisions of "Aufgaben:Exercise 4.9: Higher-Level Modulation"
| Line 16: | Line 16: | ||
*Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log<sub>2</sub>” verwendet. | *Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log<sub>2</sub>” verwendet. | ||
*Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben: | *Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben: | ||
| + | |||
[[File:P_ID2953__Inf_A_4_9_Zusatz.png|center|frame|Vorgeschlagene Signalraumkonstellationen]] | [[File:P_ID2953__Inf_A_4_9_Zusatz.png|center|frame|Vorgeschlagene Signalraumkonstellationen]] | ||
| Line 67: | Line 68: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig ist der <u>Vorschlag 2</u>, wie die Rechnung für 10 · lg (<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>) = 15 dB ⇒ <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub> = 31.62 zeigt: | '''(1)''' Richtig ist der <u>Vorschlag 2</u>, wie die Rechnung für 10 · lg (<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>) = 15 dB ⇒ <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub> = 31.62 zeigt: | ||
| − | $$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/Kanalzugriff}\hspace{0.05cm}. $$ | + | :$$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/Kanalzugriff}\hspace{0.05cm}. $$ |
Die beiden anderen Lösungsvorschläge liefern folgende Zahlenwerte: | Die beiden anderen Lösungsvorschläge liefern folgende Zahlenwerte: | ||
| − | $$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/Kanalzugriff}\hspace{0.05cm},$$ | + | :$$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/Kanalzugriff}\hspace{0.05cm},$$ |
| − | $$ C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$ | + | :$$ C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$ |
| − | Der Lösungsvorschlag 3 entspricht dabei dem Fall | + | Der Lösungsvorschlag 3 entspricht dabei dem Fall ''Zweier unabhängiger Gaußkanäle'' mit jeweils halber Sendeleistung pro Kanal. |
| − | '''(2)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u> | + | '''(2)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: |
| + | *Würde man <i>E</i><sub>S</sub> durch <i>E</i><sub>B</sub> ersetzen, so wäre auch die Aussage 3 richtig. | ||
| + | *Für <i>E</i><sub>B</sub>/<i>N</i><sub>0</sub> < ln 2 gilt nämlich <i>C</i><sub>Gauß</sub> ≡ 0 und damit auch <i>C</i><sub>BPSK</sub> ≡ 0. | ||
| − | '''(3)''' Richtig sind die <u>Aussagen 2, 3 und 5</u> | + | '''(3)''' Richtig sind die <u>Aussagen 2, 3 und 5</u>: |
| + | *Der rote Kurvenzug (<i>C</i><sub>rot</sub>) liegt stets oberhalb von <i>C</i><sub>BPSK</sub>, aber unterhalb von <i>C</i><sub>braun</sub> und der Shannon–Grenzkurve <i>C</i><sub>Gauß</sub>. | ||
| + | *Diese Aussagen gelten auch, wenn für gewisse <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>–Werte Kurven innerhalb der Zeichengenauigkeit nicht zu unterscheiden sind. | ||
| + | *Aus dem Grenzwert <i>C</i><sub>rot</sub> = 2 bit/Kanalzugriff für <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub> → ∞ kann auf den Symbolumfang <i>M<sub>X</sub></i> = 4 geschlossen werden. | ||
| + | *Die rote Kurve beschreibt also die 4–ASK. <i>M<sub>X</sub></i> = 2 würde für die BPSK gelten. | ||
| + | *Die 4–QAM führt genau zum gleichen Endwert „2 bit/Kanalzugriff”. Für kleine <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>–Werte liegt aber die Kanalkapazität <i>C</i><sub>4–QAM</sub> oberhalb der roten Kurve, da <i>C</i><sub>rot</sub> von der Gauß–Grenzkurve <i>C</i><sub>2</sub> begrenzt wird, <i>C</i><sub>4–QAM</sub> aber von <i>C</i><sub>3</sub>. | ||
| − | + | Die Bezeichnungen <i>C</i><sub>2</sub> und <i>C</i><sub>3</sub> beziehen sich hierbei auf die Teilaufgabe (1). | |
| − | |||
| − | '''(4)''' Aus dem braunen Kurvenverlauf erkennt man die Richtigkeit der beiden ersten Aussagen | + | [[File:P_ID2954__Inf_A_4_9e.png|right|frame|Kanalkapazitätsgrenzen für <br>BPSK, 4–ASK und 8–ASK]] |
| − | + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 5</u>: | |
| − | + | *Aus dem braunen Kurvenverlauf erkennt man die Richtigkeit der beiden ersten Aussagen. | |
| − | + | *Die 8–PSK mit I– und Q–Komponente – also mit <i>K</i> = 2 Dimensionen – wird für kleine <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>–Werte etwas oberhalb der braunen Kurve liegen die Antwort 3 ist falsch. | |
| − | |||
| − | + | In der Grafik sind auch die beiden 8–ASK–Systeme gemäß den Vorschlägen 4 und 5 als Punkte eingezeichnet. | |
| + | * Der violette Punkt liegt über der Kurve <i>C</i><sub>8–ASK</Sub>. Das heißt: 10 · lg (<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>) = 10 dB und <i>R</i> = 2.5 reichen nicht aus, um die 8–ASK fehlerfrei decodieren zu können ⇒ <i>R</i> > <i>C</i> ⇒ das Kanalcodierungstheorem wird nicht erfüllt ⇒ die Antwort 4 ist falsch. | ||
| + | * Reduziert man aber die Coderate gemäß dem gelben Punkt bei gleichem 10 · lg (<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>) = 10 dB auf <i>R</i> = 2 < <i>C</i><sub>8–ASK</Sub>, so wird das Kanalcodierungstheorem erfüllt ⇒ Antwort 5 ist richtig. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 14:19, 14 June 2017
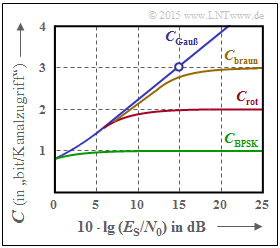
Die Grafik zeigt AWGN–Kanalkapazitätskurven über der Abszisse 10 · lg (ES/N0):
- CGauß: Shannonsche Grenzkurve,
- CBPSK: gültig für BPSK.
Die beiden weiteren Kurvenverläufe Crot und Cbraun sollen in den Teilaufgaben (c) und (d) analysiert und möglichen Modulationsverfahren zugeordnet werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
- Bezug genommen wird insbesondere auf die Seite Die Kanalkapazität C als Funktion von EB/N0.
- Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log2” verwendet.
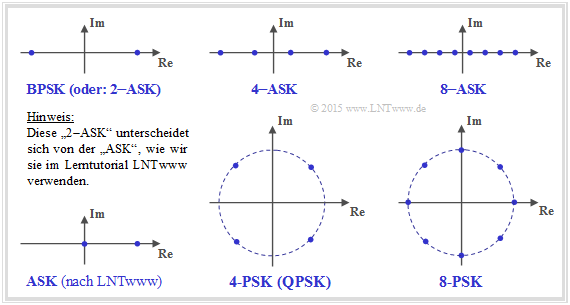
- Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben:
Anmerkungen zur Nomenklatur:
- In der Literatur wird manchmal die BPSK auch mit 2–ASK bezeichnet ⇒ x ∈ X = (+1, –1).
- Dagegen verstehen wir in unserem Lerntutorial LNTwww als ASK den unipolaren Fall x ∈ X = (0, 1).
- Nach unserer Nomenklatur gilt deshalb: CASK < CBPSK.
Dieser Sachverhalt hat aber keinen Einfluss auf die Lösung der vorliegenden Aufgabe.
Fragebogen
Musterlösung
- $$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/Kanalzugriff}\hspace{0.05cm}. $$
Die beiden anderen Lösungsvorschläge liefern folgende Zahlenwerte:
- $$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/Kanalzugriff}\hspace{0.05cm},$$
- $$ C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$
Der Lösungsvorschlag 3 entspricht dabei dem Fall Zweier unabhängiger Gaußkanäle mit jeweils halber Sendeleistung pro Kanal.
(2) Richtig sind die Lösungsvorschläge 1, 2 und 4:
- Würde man ES durch EB ersetzen, so wäre auch die Aussage 3 richtig.
- Für EB/N0 < ln 2 gilt nämlich CGauß ≡ 0 und damit auch CBPSK ≡ 0.
(3) Richtig sind die Aussagen 2, 3 und 5:
- Der rote Kurvenzug (Crot) liegt stets oberhalb von CBPSK, aber unterhalb von Cbraun und der Shannon–Grenzkurve CGauß.
- Diese Aussagen gelten auch, wenn für gewisse ES/N0–Werte Kurven innerhalb der Zeichengenauigkeit nicht zu unterscheiden sind.
- Aus dem Grenzwert Crot = 2 bit/Kanalzugriff für ES/N0 → ∞ kann auf den Symbolumfang MX = 4 geschlossen werden.
- Die rote Kurve beschreibt also die 4–ASK. MX = 2 würde für die BPSK gelten.
- Die 4–QAM führt genau zum gleichen Endwert „2 bit/Kanalzugriff”. Für kleine ES/N0–Werte liegt aber die Kanalkapazität C4–QAM oberhalb der roten Kurve, da Crot von der Gauß–Grenzkurve C2 begrenzt wird, C4–QAM aber von C3.
Die Bezeichnungen C2 und C3 beziehen sich hierbei auf die Teilaufgabe (1).
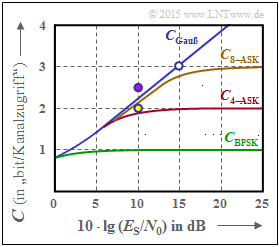
(4) Richtig sind die Lösungsvorschläge 1, 2 und 5:
- Aus dem braunen Kurvenverlauf erkennt man die Richtigkeit der beiden ersten Aussagen.
- Die 8–PSK mit I– und Q–Komponente – also mit K = 2 Dimensionen – wird für kleine ES/N0–Werte etwas oberhalb der braunen Kurve liegen die Antwort 3 ist falsch.
In der Grafik sind auch die beiden 8–ASK–Systeme gemäß den Vorschlägen 4 und 5 als Punkte eingezeichnet.
- Der violette Punkt liegt über der Kurve C8–ASK. Das heißt: 10 · lg (ES/N0) = 10 dB und R = 2.5 reichen nicht aus, um die 8–ASK fehlerfrei decodieren zu können ⇒ R > C ⇒ das Kanalcodierungstheorem wird nicht erfüllt ⇒ die Antwort 4 ist falsch.
- Reduziert man aber die Coderate gemäß dem gelben Punkt bei gleichem 10 · lg (ES/N0) = 10 dB auf R = 2 < C8–ASK, so wird das Kanalcodierungstheorem erfüllt ⇒ Antwort 5 ist richtig.