Difference between revisions of "Aufgaben:Exercise 2.8: Asymmetrical Channel"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1038__Mod_A_2_8.png|right|]] | + | [[File:P_ID1038__Mod_A_2_8.png|right|frame|Äquivalentes Tiefpass–Signal in der komplexen Ebene]] |
| − | Ein cosinusförmiges Quellensignal $q(t)$ mit der Amplitude $ | + | Ein cosinusförmiges Quellensignal $q(t)$ mit der Amplitude $A_{\rm N}$ und der Frequenz $f_{\rm N}$ wird ZSB–amplitudenmoduliert, so dass für das modulierte Signal gilt: |
| − | $$ s(t) = | + | :$$ s(t) = [ q(t) + A_{\rm T}] \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$ |
| − | Der Übertragungskanal weist lineare Verzerrungen auf. Während sowohl das untere Seitenband als auch der Träger unverfälscht übertragen werden, wird das obere Seitenband (bei der OSB-Frequenz $ | + | Der Übertragungskanal weist lineare Verzerrungen auf. Während sowohl das untere Seitenband (bei der USB-Frequenz $f_{\rm T} - f_{\rm N}$) als auch der Träger unverfälscht übertragen werden, wird das obere Seitenband (bei der OSB-Frequenz $f_{\rm T} + f_{\rm N}$) mit dem Dämpfungsfaktor $α_{\rm O} = 0.25$ gewichtet. |
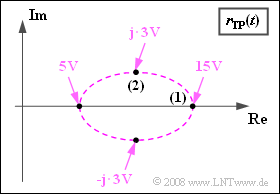
| − | Die Grafik zeigt die Ortskurve, also die Darstellung des äquivalenten Tiefpass–Signals $ | + | Die Grafik zeigt die Ortskurve, also die Darstellung des äquivalenten Tiefpass–Signals $r_{\rm TP}(t)$ in der komplexen Ebene. |
| − | |||
| − | |||
| − | In der Teilaufgabe | + | Wertet man das Signal $r(t)$ mit einem idealen Hüllkurvendemodulator aus, so erhält man ein Sinkensignal $v(t)$, das wie folgt angenähert werden kann: |
| − | $$ \rho_{v } = \frac{P_{v 1}}{P_{\varepsilon }} \hspace{0.05cm}.$$ | + | :$$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )-\text{ ...}$$ |
| − | Hierbei bezeichnen $P_{ | + | Für diese Messung wurde die Nachrichtenfrequenz $f_{\rm N} = 2 \ \rm kHz$ benutzt. |
| − | $$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$ | + | |
| − | $$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$ | + | In der Teilaufgabe (7) soll das Signal–zu–Stör–Leistungsverhältnis (SNR) wie folgt berechnet werden: |
| + | :$$ \rho_{v } = \frac{P_{v 1}}{P_{\varepsilon }} \hspace{0.05cm}.$$ | ||
| + | Hierbei bezeichnen $P_{v1} = α^2 · P_q$ und $P_ε$ die „Leistungen” der beiden Signale: | ||
| + | :$$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$ | ||
| + | :$$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Hüllkurvendemodulation|Hüllkurvendemodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf das Kapitel [[Modulationsverfahren/Hüllkurvendemodulation#Beschreibung_mit_Hilfe_des_.C3.A4quivalenten_TP.E2.80.93Signals|Beschreibung mit Hilfe des äquivalenten Tiefpass-Signals]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Line 25: | Line 32: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie $r_{TP}(t)$ in analytischer Form an. Welcher Wert ergibt sich für t = 0? | + | {Geben Sie das Tiefpass-Signal $r_{\rm TP}(t)$ in analytischer Form an. Welcher Wert ergibt sich für die Zeit $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $r_{TP}(t=0)$ | + | $r_{\rm TP}(t=0) \ = \ $ { 15 3% } $\ \rm V$ |
| − | { | + | {Wie lauten die Amplitudenwerte $A_{\rm T}$ und $A_{\rm N}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_{\rm T} \ = \ $ { 10 3% } $\ \rm V$ |
| − | $ | + | $A_{\rm N} \ = \ $ { 8 3% } $\ \rm V$ |
| − | {Es gelte $ | + | {Es gelte $f_{\rm N} = 2 \ \rm kHz$. Zu welcher Zeit $t_1$ wird der Startpunkt '''(1)''' zum ersten Mal nach $t = 0$ wieder erreicht? |
|type="{}"} | |type="{}"} | ||
| − | $t_1$ | + | $t_1 \ = \ $ { 0.5 3% } $\ \rm ms$ |
| − | {Zu welchem Zeitpunkt $t_2$ wird der Ellipsenpunkt (2) mit dem Wert $j · 3 V$ zum ersten Mal erreicht? | + | {Zu welchem Zeitpunkt $t_2$ wird der Ellipsenpunkt '''(2)''' mit dem Wert $j · 3\ \rm V$ zum ersten Mal erreicht? |
|type="{}"} | |type="{}"} | ||
| − | $t_2$ | + | $t_2 \ = \ $ { 0.375 3% } $\ \rm ms$ |
| − | {Berechnen Sie die | + | {Berechnen Sie die Betragsfunktion (Hüllkurve) $a(t)$ und die Phasenfunktion $ϕ$ für diesen Zeitpunkt $t_2$. |
|type="{}"} | |type="{}"} | ||
| − | $a(t = t_2)$ | + | $a(t = t_2) \ = \ $ { 10.44 3% } $\ \rm V$ |
| − | $ϕ(t = t_2)$ | + | $ϕ(t = t_2)\ = \ $ { 16.7 3% } $\ \rm Grad$ |
| − | {Berechnen Sie den Klirrfaktor für $ | + | {Berechnen Sie den Klirrfaktor $K$ für $f_{\rm N} = 2 \ \rm kHz$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm N} = 2 \ \rm kHz\text{:}$ $K \ = \ $ { 6.6 3% } $\ \text{%}$ |
| − | {Berechnen Sie für $ | + | {Berechnen Sie für $f_{\rm N} = 2 \ \rm kHz$ das Signal–zu–Stör–Leistungsverhältnis (SNR) gemäß der angegebenen Definition. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm N} = 2 \ \rm kHz\text{:}$ $ρ_v \ = \ $ { 230 3% } |
| − | { Welcher Klirrfaktor K ergibt sich bei ansonsten gleichen Bedingungen mit der Nachrichtenfrequenz $ | + | { Welcher Klirrfaktor $K$ ergibt sich bei ansonsten gleichen Bedingungen mit der Nachrichtenfrequenz $f_{\rm N} = 4 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm N} = 4 \ \rm kHz\text{:}$ $K \ = \ $ { 6.6 3% } $\ \text{%}$ |
</quiz> | </quiz> | ||
Revision as of 17:35, 30 June 2017
Ein cosinusförmiges Quellensignal $q(t)$ mit der Amplitude $A_{\rm N}$ und der Frequenz $f_{\rm N}$ wird ZSB–amplitudenmoduliert, so dass für das modulierte Signal gilt:
- $$ s(t) = [ q(t) + A_{\rm T}] \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$
Der Übertragungskanal weist lineare Verzerrungen auf. Während sowohl das untere Seitenband (bei der USB-Frequenz $f_{\rm T} - f_{\rm N}$) als auch der Träger unverfälscht übertragen werden, wird das obere Seitenband (bei der OSB-Frequenz $f_{\rm T} + f_{\rm N}$) mit dem Dämpfungsfaktor $α_{\rm O} = 0.25$ gewichtet.
Die Grafik zeigt die Ortskurve, also die Darstellung des äquivalenten Tiefpass–Signals $r_{\rm TP}(t)$ in der komplexen Ebene.
Wertet man das Signal $r(t)$ mit einem idealen Hüllkurvendemodulator aus, so erhält man ein Sinkensignal $v(t)$, das wie folgt angenähert werden kann:
- $$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )-\text{ ...}$$
Für diese Messung wurde die Nachrichtenfrequenz $f_{\rm N} = 2 \ \rm kHz$ benutzt.
In der Teilaufgabe (7) soll das Signal–zu–Stör–Leistungsverhältnis (SNR) wie folgt berechnet werden:
- $$ \rho_{v } = \frac{P_{v 1}}{P_{\varepsilon }} \hspace{0.05cm}.$$
Hierbei bezeichnen $P_{v1} = α^2 · P_q$ und $P_ε$ die „Leistungen” der beiden Signale:
- $$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$
- $$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Hüllkurvendemodulation.
- Bezug genommen wird insbesondere auf das Kapitel Beschreibung mit Hilfe des äquivalenten Tiefpass-Signals.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Die Trägeramplitude ist durch den Ellipsenmittelpunkt festgelegt: $A_T = 10 V$. Aus der bei Punkt a) angegebenen Gleichung kann somit auch die Amplitude $A_N$ berechnet werden:
$$ \frac{A_{\rm N}}{2} \cdot ( 1+ \alpha_0) = r_{\rm TP}(t= 0) - A_{\rm T} = 5 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} \hspace{0.15cm}\underline {= 8 \,{\rm V}} \hspace{0.05cm}.$$
Zur Kontrolle kann der Punkt (2) in der Grafik herangezogen werden:
$$\frac{A_{\rm N}}{2} \cdot ( 1- \alpha_0) = 3 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} = 8 \,{\rm V} \hspace{0.05cm}.$$
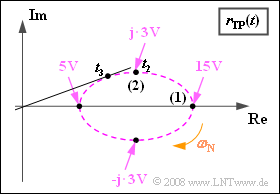
3.Die für einen Umlauf benötigte Zeit t1 ist gleich der Periodendauer des Quellensignals, also 0.5 ms.
4.Da das USB größer ist als das OSB, bewegt sich die Spitze des Zeigerverbundes auf der Ellipse im Uhrzeigersinn. Der Punkt (2) wird zum Zeitpunkt $t_2 = 3/4 · t_1 = 0.375 ms$ zum ersten Mal erreicht.
5. Die Zeigerlänge zum Zeitpunkt t2 kann mit dem Satz von Pythagoras bestimmt werden: $$ a(t = t_2) = \sqrt{(10 \,{\rm V})^2 + (3 \,{\rm V})^2}\hspace{0.15cm}\underline { = 10.44 \,{\rm V}}\hspace{0.05cm}.$$ Für die Phasenfunktion gilt: $$\phi(t = t_2) = {\rm arctan} \frac{3 \,{\rm V}}{10 \,{\rm V}} \hspace{0.15cm}\underline {= 16.7^{\circ}}\hspace{0.05cm}.$$ Die maximale Phase $ϕ_{max}$ ist geringfügig größer. Sie tritt (mit positivem Vorzeichen) zum Zeitpunkt $t_3 < t_2$ dann auf, wenn eine Gerade vom Koordinatenursprung die Ellipse tangiert. Durch Aufstellen der Ellipsengleichung kann dieser Punkt ($x_3$, $y_3$) analytisch exakt berechnet werden. Daraus würde für die maximale Phase gelten: $$\phi_{\rm max} = {\rm arctan} \frac{y_3}{x_3} \hspace{0.05cm}.$$
6. Die Klirrfaktoren zweiter und dritter Ordnung lauten:
$$ K_2 = \frac{0.148 \,{\rm V}}{2.424 \,{\rm V}} = 0.061, \hspace{0.3cm} K_3 = \frac{0.056 \,{\rm V}}{2.424 \,{\rm V}} = 0.023 \hspace{0.05cm}.$$
Damit erhält man für den Gesamtklirrfaktor:
$$K = \sqrt{K_2^2 + K_3^2 }\hspace{0.15cm}\underline { \approx 6.6 \%}.$$
7.Für die Leistungen von Nutz– und Störsignal erhält man:
$$ P_{v 1} = \frac{(2.424 \,{\rm V})^2}{2} = 2.94 \,{\rm V}^2\hspace{0.05cm},$$
$$ P_{\varepsilon} = \frac{(-0.148 \,{\rm V})^2}{2} + \frac{(0.056 \,{\rm V})^2}{2}= 0.0125 \,{\rm V}^2\hspace{0.05cm}$$
Damit ergibt sich:
$$\rho_{v 1 } = \frac{P_{v 1}}{P_{\varepsilon }}= \frac{(2.94 \,{\rm V})^2}{0.0125 \,{\rm V}^2} \hspace{0.15cm}\underline {\approx 230} = \frac{1}{K^2} \hspace{0.05cm}.$$
Würde man dagegen die Amplitudenverfälschung ebenfalls dem Fehlersignal zuweisen, so käme man zu einem deutlich kleineren SNR. Mit $P_q = A_N^2/2 = 8 V^2$ und
$$P_{\varepsilon}\hspace{0.02cm}' = \overline{(v(t)-q(t))^2} = \frac{1}{2}\cdot ( 4 \,{\rm V} - 2.424 \,{\rm V})^2 + P_{\varepsilon}= 1.254 \,{\rm V}^2$$
würde man erhalten:
$$\rho_{v }\hspace{0.02cm}' = \frac{8 \,{\rm V}^2}{1.254 \,{\rm V}^2} \approx 6.4\hspace{0.05cm}.$$
8. Alle Berechnungen gelten unabhängig von der Nachrichtenfrequenz $f_N$, wenn der Dämpfungsfaktor des OSB weiterhin $α_O = 0.25$ beträgt. Dann erhält man ebenfalls $K ≈ 6.6%$.