Aufgaben:Exercise 2.12: Non-coherent Demodulation

• Return to book

Nichtkohärente ASK–Demodulation

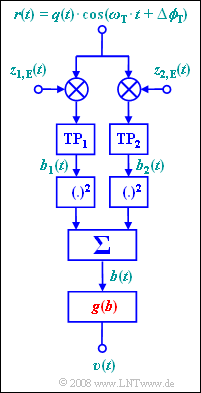
Wir betrachten ein AM–moduliertes Signal:

$$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$

Den Empfänger erreicht aufgrund der Kanallaufzeit das Signal

$$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$

Die nebenstehende Anordnung erlaubt eine perfekte Demodulation – das heißt $v(t) = q(t)$ – ohne Kenntnis der Phase $Δϕ_T$, allerdings nur dann, wenn das Quellensignal $q(t)$ gewisse Voraussetzungen erfüllt.

Die beiden empfängerseitigen Trägersignale lauten:

$$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$

$$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$

$\rm TP_1$ und $\rm TP_2$ bezeichnen zwei ideale Tiefpässe, deren Grenzfrequenz jeweils gleich der Trägerfrequenz $f_{\rm T}$ ist. Die nichtlineare Funktion $v = g(b)$ soll im Rahmen dieser Aufgabe ermittelt werden.

Als (digitale) Quellensignale werden betrachtet:

• das unipolare Rechtecksgnal $q_1(t)$ mit den dimensionslosen Amplitudenwerten $0$ und $3$,
• das bipolare Rechtecksignal $q_2(t)$ mit den dimensionslosen Amplitudenwerten $±3$.

Diese beiden Signale ergeben hinsichtlich $s(t)$ ein ASK–Signal bzw. ein BPSK–Signal.

Hinweise:

• Die Aufgabe gehört zum Kapitel WeitereAM–Variantenn.
• Bezug genommen wird insbesondere auf die Inkohärente (nichtkohärente) Demodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gegeben sind folgende trigonometrischen Umformungen:

$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \left[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \right],$$

$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \left[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \right],$$

$$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \left[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \right] \hspace{0.05cm}.$$

Fragebogen

1

Wie lauten die Signale $b_1(t)$ und $b_2(t)$ in den beiden Zweigen – jeweils nach Multiplizierer und Tiefpass? Welche Aussagen treffen zu?

	$b_1(t) = q(t) · \cos(Δϕ_{\rm T})$.
	$b_2(t) = q(t) · \cos(Δϕ_{\rm T})$.
	$b_1(t) = q(t) · \sin(Δϕ_{\rm T})$.
	$b_2(t) = q(t) · \sin(Δϕ_{\rm T})$.
	$b_1(t) = b_2(t) = q(t)$.

2

Welche Werte $b_{\rm min}$ und $b_{\rm max}$ nimmt das Signal $b(t)$ an, wenn am Eingang das unipolare Quellensignal $q_1(t)$ anliegt?

$b_{\rm min} \ = \ $

$b_{\rm max} \ = \ $

3

Wie muss die Kennlinie $v = g(b)$ gewählt werden, damit $v(t) = q(t)$ gilt?

	$v=g(b) = b^2$.
	$v=g(b) = \sqrt{b}$.
	$v=g(b) = \arctan(b).$

4

Welche Werte $b_{\rm min}$ und $b_{\rm max}$ nimmt das Signal $b(t)$ an, wenn am Eingang das bipolare Quellensignal $q_2(t)$ anliegt?

$b_{\rm min} \ = \ $

$b_{\rm max} \ = \ $

Musterlösung

Solution

(1)  Durch Anwendung der auf der Angabenseite gegebenen trigonometrischen Umformungen erhält man unter Berücksichtigung der beiden Tiefpässe (die Anteile um die doppelte Trägerfrequenz werden entfernt):

$$b_1(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot 2 \cdot \cos(\omega_{\rm T} \cdot t) = q(t) \cdot \cos(\Delta \phi_{\rm T})\hspace{0.05cm},$$

$$ b_2(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot (-2) \cdot \sin(\omega_{\rm T} \cdot t) = q(t) \cdot \sin(\Delta \phi_{\rm T})\hspace{0.05cm}.$$

Richtig sind somit die erste und die vierte Antwort.

(2)  Die Summe der Quadrate der beiden Teilsignale ergibt:

$$ b(t) = b_1^2(t) + b_2^2(t)= q^2(t) \cdot \left( \cos^2(\Delta \phi_{\rm T})+ \sin^2(\Delta \phi_{\rm T})\right) = q^2(t)\hspace{0.05cm}.$$

Die möglichen Amplitudenwerte sind somit:   $b_{\rm min}\hspace{0.15cm}\underline{ = 0},\hspace{0.3cm} b_{\rm max}\hspace{0.15cm}\underline{ =9}.$

'(3)  Richtig ist der zweite Lösungsvorschlag:

$$v=g(b) = \sqrt{b} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t) = \sqrt{ q^2(t) } = q(t)\hspace{0.05cm}.$$

(4)  Das Ergebnis $b(t) = q^2(t)$ – siehe Teilaufgabe (2) – führt hier zum Ergebnis:   $b_{\rm min}\hspace{0.15cm}\underline{ = 9},\hspace{0.3cm} b_{\rm max}\hspace{0.15cm}\underline{ =9}.$
Dies zeigt, dass der hier betrachtete Demodulator nur dann funktioniert, wenn für alle Zeiten $q(t) ≥ 0$ oder $q(t) ≤ 0$ gilt und dies dem Empfänger auch bekannt ist.