Aufgaben:Exercise 4.8: Different Error Probabilities

• Return to book

AWGN–Fehlerwahrscheinlichkeitskurven von ASK, BPSK und DPSK

Hier werden die Bitfehlerwahrscheinlichkeiten $p_{\rm B}$ der digitalen Modulationsverfahren ASK und BPSK ohne weitere Herleitung angegeben. Beispielsweise erhält man mit der so genannten Q–Funktion

$$ \rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\cdot \int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u$$

für den AWGN–Kanal – gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$ – und weiteren optimalen Voraussetzungen (zum Beispiel kohärente Demodulation)

• für Amplitude Shift Keying (ASK):

$$ p_{\rm B} = {\rm Q}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm},$$

• für Binary Phase Shift Keying (BPSK):

$$ p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm}.$$

Die entsprechende Gleichung für Differential Phase Shift Keying (DPSK) mit differentiell–kohärenter Demodulation lautet:

$$p_{\rm B} ={1}/{2} \cdot {\rm e}^{- E_{\rm B}/{N_0 }}\hspace{0.05cm}.$$

Aber auch die ASK könnte nichtkohärent demoduliert werden. In diesem Fall würde gelten:

$$ p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/(2{N_0 })}\hspace{0.05cm}.$$

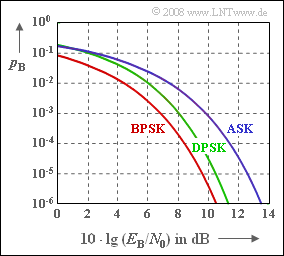
Die drei ersten Fehlerwahrscheinlichkeiten sind in der Grafik dargestellt. Beispielsweise erhält man für $10 · \lg E_{\rm B}/N_0 = 10 \ \rm dB$ entsprechend den exakten Funktionen:

$$ p_{\rm B} = 7.83 \cdot 10^{-4}\,\,{\rm (ASK)}\hspace{0.05cm},\hspace{0.3cm} p_{\rm B} = 3.87 \cdot 10^{-6}\,\,{\rm (BPSK)}\hspace{0.05cm},$$

Um bei BPSK die Bitfehlerwahrscheinlichkeit $p_B = 10^{–5}$ zu erreichen bzw. zu unterschreiten, muss $10 · \lg E_{\rm B}/N_0 \ge 9.6 \ \rm dB$ sein.

Hinweise:

• Die Aufgabe gehört zum Kapitel Lineare digitale Modulation.
• Bezug genommen wird insbesondere auf die Seite Fehlerwahrscheinlichkeiten - ein kurzer Überblick.
• Die Herleitungen finden Sie im Kapitel Lineare digitale Modulation – Kohärente Demodulation desBuches „Digitalsignalübertragung”.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Für die numerischen Auswertungen können Sie die folgende obere Schranke verwenden:

$$ \rm Q_{\rm S} (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi} \cdot x}\cdot \rm e^{\it -x^{\rm 2}/\rm 2} \ge \rm Q (\it x)\hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie die ASK–Bitfehlerwahrscheinlichkeit für $10 · \lg E_{\rm B}/N_0 = 10 \ \rm dB$ unter Verwendung der oberen Schranke ${\rm Q_S}(x)$.

$p_{\rm B} \ = \ $ $\ \cdot 10^{-5}$

2

Berechnen Sie die BPSK–Bitfehlerwahrscheinlichkeit für $10 · \lg E_{\rm B}/N_0 = 10 \ \rm dB$ unter Verwendung der oberen Schranke ${\rm Q_S}(x)$.

$p_{\rm B} \ = \ $ $\ \cdot 10^{-5}$

3

Geben Sie für die ASK den minimalen Wert für $E_{\rm B}/N_0$ (in dB) an, damit die Bitfehlerwahrscheinlichkeit $p_{\rm B} = 10^{–5}$ erreicht wird.

$10 · \lg E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

4

Berechnen Sie die DPSK–Bitfehlerwahrscheinlichkeit für $10 · \lg E_{\rm B}/N_0 = 10 \ \rm dB$.

$p_{\rm B} \ = \ $ $\ \cdot 10^{-5}$

5

Geben Sie für DPSK den minimalen Wert für $E_{\rm B}/N_0$ (in dB) an, damit die Bitfehlerwahrscheinlichkeit $p_{\rm B} = 10^{–5}$ erreicht wird

$10 · \lg E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

6

Welches $E_{\rm B}/N_0$ (in dB) benötigt man dagegen bei inkohärenter ASK, um wieder $p_{\rm B} = 10^{–5}$ zu erreichen?

$10 · \lg E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Aus $10 · \lg E_{\rm B}/N_0 = 10 \ \rm dB$ folgt $ E_{\rm B}/N_0 = 10 $ und damit

$$p_{\rm B} = {\rm Q}\left ( \sqrt{10} \right ) \approx {\rm Q_{\rm S}}\left ( \sqrt{10} \right )= \frac{\rm 1}{\sqrt{\rm 20\pi} }\cdot \rm e^{-5 }\hspace{0.15cm}\underline {= 85 \cdot 10^{-5}}\hspace{0.05cm}.$$

Der tatsächliche Wert gemäß dem Angabenblatt lautet $7.83 · 10^{–4}$. Die angegebene Gleichung ${\rm Q_S}(x)$ ist also tatsächlich eine obere Schranke für ${\rm Q}(x)$. Der relative Fehler bei Verwendung von ${\rm Q_S}(x)$ anstelle von ${\rm Q}(x)$ ist in diesem Fall kleiner als $10\%$.

(2)  Bei BPSK lautet die entsprechende Gleichung:

$$ p_{\rm B} = {\rm Q}\left ( \sqrt{20} \right ) \approx {\rm Q_{\rm S}}\left ( \sqrt{20} \right )= \frac{\rm 1}{\sqrt{\rm 40\pi} }\cdot \rm e^{-10 }\hspace{0.15cm}\underline {= 0.405 \cdot 10^{-5}}\hspace{0.05cm}.$$

• Nun beträgt der relative Fehler durch Verwendung von ${\rm Q_S}(x)$ nur noch $\5\%$.
• Allgemein gilt: Je kleiner die Fehlerwahrscheinlichkeit ist, um so besser ist die Näherung ${\rm Q}(x) ≈ {\rm Q_S}(x)$.

(3)  Bei BPSK ist hierfür laut Angabe ein (logarithmierter) Wert von $9.6\ \rm dB$ erforderlich. Bei der ASK muss der logarithmierte Wert um etwa $3\ \rm dB$ erhöht werden   ⇒   $10 · \lg E_{\rm B}/N_0 \hspace{0.15cm}\underline {= 12.6 \ \rm dB}$.

(4)  Entsprechend der angegebenen DPSK–Gleichung gilt mit $ E_{\rm B}/N_0 = 10 $:

$$p_{\rm B} = {\rm 1}/{2 }\cdot \rm e^{-10 }\hspace{0.15cm}\underline {\approx 2.27 \cdot 10^{-5}}\hspace{0.05cm}.$$

Wie bereits aus der Grafik auf der Angabenseite ersichtlich, liegt die DPSK mit differentiell–kohärenter Demodulation zwischen der binären Phasenmodulation (BPSK) und der binären Amplitudenmodulation (ASK), wenn für beide eine kohärente Demodulation vorgesehen ist.

(5)  Aus der Umkehrfunktion der angegebenen Gleichung erhält man:

$$ \frac{E_{\rm B}} {N_{\rm 0}}= {\rm ln}\hspace{0.1cm}\frac{1}{2 p_{\rm B}}= {\rm ln}(50000)\approx 10.82 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\frac{E_{\rm B}} {N_{\rm 0}}\hspace{0.15cm}\underline {\approx 10.4\,\,{\rm dB}}\hspace{0.05cm}.$$

(6)  Die inkohärente ASK ist entsprechend den angegebenen Gleichungen wieder um $3\ \rm dB$ schlechter als die differentiell–kohärente DPSK. Daraus folgt für den gesuchten dB–Wert:   $10 · \lg E_{\rm B}/N_0 \hspace{0.15cm}\underline {≈ 13.4 \ \rm dB}$.