Aufgaben:Exercise 1.1: Basic Transmission Pulses

• Return to book

Sendegrundimpulse

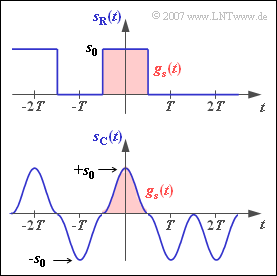
Wir untersuchen in dieser Aufgabe die zwei in der Grafik dargestellten Sendesignale $s_{\rm R}(t)$ und $s_{\rm C}(t)$ mit Rechteck– bzw. cos2–Sendegrundimpuls. Insbesondere sollen für die jeweiligen Impulse $g_s(t)$ folgende Kenngrößen berechnet werden:

• die äquivalente Impulsdauer von $g_s(t)$:

$$\Delta t_{\rm S} = \frac {\int ^{+\infty} _{-\infty} \hspace{0.15cm} g_s(t)\,{\rm d}t}{{\rm Max} \hspace{0.05cm}[g_s(t)]} \hspace{0.05cm},$$

• die Energie des Sendegrundimpulses $g_s(t)$:

$$E_g = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t \hspace{0.05cm},$$

• die Leistung des Sendesignals $s(t)$:

$$P_{\rm S} = \lim_{T_{\rm M} \to \infty} \frac{1}{+T_{\rm M}} \cdot \int^{+T_{\rm M}/2} _{-T_{\rm M}/2} s^2(t)\,{\rm d}t \hspace{0.05cm}.$$

Gehen Sie bei Ihren Berechnungen stets davon aus, dass die beiden möglichen Amplitudenkoeffizienten gleichwahrscheinlich sind und dass der Abstand zwischen benachbarten Symbolen $T = 1 \ \rm μs$ beträgt. Dies entspricht einer Bitrate von $R = 1 \ \rm Mbit/s$.

• Der (positive) Maximalwert des Sendesignals ist in beiden Fällen gleich

$$s_0 = \sqrt{0.5\, {\rm W}} \hspace{0.05cm}.$$

• Unter der Annahme, dass der Sender mit einem Widerstand von 50 Ω abgeschlossen ist, entspricht dies dem folgenden Spannungswert:

s_0 = \sqrt{0.5\, {\rm W}} \hspace{0.05cm}.

Hinweise:

• Die Aufgabe gehört zum Kapitel Systemkomponenten eines Basisbandübertragungssystems.
• Bezug genommen wird insbesondere auf den AbschnittKenngrößen des digitalen Senders.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gegeben ist das folgende unbestimmte Integral:

$$\int \cos^4(a x)\,{\rm d}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin(2 a x)+ \frac{1}{32a} \cdot \sin(4 a x)\hspace{0.05cm}.$$

Fragebogen

1

Handelt es sich bei $s_{\rm R}(t)$ und $s_{\rm C}(t)$ um unipolare oder bipolare Signale?

	$s_{\rm R}(t)$ ist ein bipolares Signal.
	$s_{\rm c}(t)$ ist ein bipolares Signal.

2

Wie groß ist die äquivalente Impulsdauer $\Delta t_{\rm S}$, normiert auf die Symboldauer $T$?

$\text{Beim Signal}\ s_{\rm R}(t) \text{:} \ \ \Delta t_{\rm S}/T \ = \ $

$\text{beim Signal}\ s_{\rm C}(t) \text{:} \ \ \Delta t_{\rm S}/T \ = \ $

3

Wie groß ist die Energie des rechteckförmigen Sendegrundimpulses??

$E_g \ = \ $ $\ \cdot 10^{-6}\ \rm Ws$

4

Wie groß ist die Leistung des rechteckförmigen Sendesignals $s_{\rm R}(t)$?

$P_{\rm S} \ = \ $ $\ \rm W$

5

Wie groß ist die Energie des $\cos^2–Sendegrundimpulses?

$E_g \ = \ $ $\ \cdot 10^{-6}\ \rm Ws$

6

Wie groß ist die Leistung des rechteckförmigen Sendesignals $s_{\rm C}(t)$?

$P_{\rm S} \ = \ $ $\ \rm W$

Musterlösung

Solution

(1)  Aus der Gesamtbandbreite 24.8 MHz und dem Kanalabstand 200 kHz folgt $K_{\rm F}\hspace{0.15cm}\underline{ = 124}$.

(2)  Die Mittenfrequenz des ersten Kanals liegt bei 890.2 MHz. DerKanal „RFCH 100” liegt um 99 · 200 kHz = 19.8 MHz höher:

$$f_{\rm M}= 890.2 \ \rm MHz + 19.8 \ \rm MHz\hspace{0.15cm}\underline{ = 910 \ \rm MHz}.$$

(3)  Um die Überlegungen zur Teilaufgabe (2) nutzen zu können, transformieren wir die Aufgabenstellung in den Uplink: Der gleiche Kanal mit der Kennung $k_{\rm F}$, der im Downlink die Frequenz 940 MHz nutzt, liegt im Uplink bei 895 MHz. Damit gilt:

$$k_{\rm F} = 1 + \frac {895 \,\,{\rm MHz } - 890.2 \,\,{\rm MHz } }{0.2 \,\,{\rm MHz }} \hspace{0.15cm}\underline {= 25}.$$

(4)  In einem TDMA–Rahmen der Dauer 4.62 Millisekunden können $K_{\rm T}\hspace{0.15cm}\underline{ = 8}$ Zeitschlitze mit jeweiliger Dauer $T = 577 \ \rm μs$ untergebracht werden. Anmerkung: Bei GSM wird tatsächlich $K_{\rm T} = 8$ verwendet.

(5)  Mit den Ergebnissen der Teilaufgaben (1) und (4) erhält man:

$$K = K_{\rm F} \cdot K_{\rm T} = 124 \cdot 8 \hspace{0.15cm}\underline {= 992}$$

(6)  Während der Zeit $T = 577 \ \rm μs$ müssen 156 Bit übertragen werden. Damit stehen für jedes Bit die Zeit $T_{\rm B} = 3.699 \ \rm μs$ zur Verfügung. Daraus ergibt sich die (Brutto–)Bitrate

$$R_{\rm Brutto} = \frac {1 }{T_{\rm B}}\hspace{0.15cm}\underline {\approx 270 \,\,{\rm kbit/s }}.$$

Diese Brutto–Bitrate beinhaltet neben den das Sprachsignal beschreibenden Datensymbolen auch die Trainigssequenz zur Kanalschätzung und die Redundanz für die Kanalcodierung. Die Netto–Bitrate beträgt beim GSM–System für jeden der acht Benutzer nur etwa 13 kbit/s.