Aufgaben:Exercise 5.6: OFDM Spectrum

• Return to book

Real- und Imaginärteil des OFDM-Signals

Wir betrachten hier ein OFDM–System mit $N = 4$ Trägern. Zur Vereinfachung beschränken wir uns auf ein einziges Zeitintervall $T$ und gehen auch von der Rahmendauer $T_{\rm R} = T$ aus. Ein Guard–Intervall wird demnach nicht verwendet.

Mit der Zusammenfassung von Impulsformung und Modulation durch die gemeinsame Funktion

$$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$

ergibt sich das (komplexe) OFDM–Sendesignal im betrachteten Zeitintervall ($0 ≤ t < T$) zu:

$$s (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu} \cdot g_\mu (t )}.$$

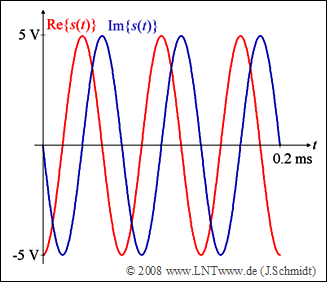
Alle Trägerkoeffizienten $a_0$, $a_1$, $a_2$ und $a_3$ sind entweder $0$ oder $\pm 1$.. Die Grafik zeigt den Real– und Imaginärteil des Sendesignals $s(t)$ für eine gegebene Kombination von $a_0$, ... , $a_3$, die in der Teilaufgabe (3) ermittelt werden soll.

Hinweise:

• Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung von OFDM.
• Bezug genommen wird aber auch auf das Kapitel Zielsetzung von Modulation und Demodulationund das Kapitel Global System for Mobile Communications (GSM) im Buch „Beispiele_von_Nachrichtensystemen”.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Hinweise:

• Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung von OFDM.
• Bezug genommen wird insbesondere auf die Seiten OFDM-Systembetrachtung im Zeitbereich sowie OFDM-Systembetrachtung im Frequenzbereich bei kausalem Grundimpuls.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie groß ist die Amplitude $s_0$?

$s_0$ = $V$

2

Wie groß ist die Symboldauer T?

$T$ = $ms$

3

Welche Amplitudenkoeffizienten liegen der Grafik zugrunde?

$a_0$ =

$a_1$ =

$a_3$ =

4

Welche Aussagen sind bezüglich der OFDM–Betragsfunktion |s(t)| zutreffend?

	$|s(t)|$ ist konstant ohne Begrenzung.
	$|s(t)|$ ist konstant innerhalb von T.
	$|s(t)|$ besitzt einen cosinusförmigen Verlauf.
	$|s(t)|$ besitzt einen sinusförmigen Verlauf.

5

Nun sei a₀ = 0, a₁ = +1, a₂ = –1 und a₃ = +1. Berechnen Sie das Spektrum S(f). Welche Werte ergeben sich für die nachfolgend genannten Frequenzen?

$S(f = 0)$ = $V/Hz$

$S(f = 5 KHz)$ = $10^{-3}$ $V/Hz$

$S(f = 10 KHz)$ = $10^{-3}$ $V/Hz$

$S(f = 15 KHz)$ = $10^{-3}$ $V/Hz$

6

Interpretieren Sie Ihre Ergebnisse zu c) und e). Welche Aussagen treffen zu?

	OFDM erfüllt das erste Nyquist–Kriterium im Zeitbereich.
	OFDM erfüllt das erste Nyquist–Kriterium im Frequenzbereich.

Musterlösung

Solution

1. Das Sendesignal $s(t)$ ist eine komplexe Exponentialschwingung mit nur einer Frequenz. Die Amplitude $s_0 = 5 V$ kann direkt der Grafik entnommen werden.

2. Weiterhin erkennt man aus der Grafik die Symboldauer $T = 0.2 ms$. Daraus ergibt sich die Grundfrequenz zu $f_0 = 1/T = 5 kHz$.

3. Im dargestellten Beispiel gibt es nur eine einzige Frequenz $3 · f_0$. Daraus folgt $a_0 = a_1 = a_2 = 0$ sowie für den Bereich 0 ≤ t < T: $$s(t) = a_3 \cdot s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2 \pi}} \hspace{0.04cm}\cdot \hspace{0.04cm} 3 f_0 \hspace{0.04cm}\cdot \hspace{0.04cm} t}= a_3 \cdot s_0 \cdot \cos ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \rm{j} \cdot a_3 \cdot s_0 \cdot \sin ({\rm{2 \pi}} \cdot 3 f_0 \cdot t).$$ Der Vergleich mit der Skizze (Realteil: Minus–Cosinus, Imaginärteil: Minus–Sinus) liefert das folgende Ergebnis: $a_3 = –1$.

4. Richtig ist der zweite Lösungsvorschlag. Die Betragsfunktion lautet: $$|s(t)| = a_3 \cdot s_0 \cdot \sqrt{\cos^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t) + \sin^2 ({\rm{2 \pi}} \cdot 3 f_0 \cdot t)}= a_3 \cdot s_0.$$ Allerdings gilt diese Gleichung nur im Bereich der Symboldauer T. Das OFDM–Prinzip funktioniert nur bei einer Zeitbegrenzung auf T.

5. Allgemein gilt für das OFDM–Spektrum: $$S (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu } \cdot \,} {\rm{si}}(\pi \cdot T \cdot (f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi}} \hspace{0.04cm}\cdot \hspace{0.04cm}{T}/{2}\hspace{0.04cm}\cdot \hspace{0.04cm} (f - \mu \cdot f_0 )} .$$ Die si–Funktion ergibt sich aus der zeitlichen Begrenzung auf T, der letzte Term in der Summe aus dem Verschiebungssatz. Durch die Nulldurchgänge der si–Funktion im Abstand $f_0$ sowie $si(0) = 1$ erhält man $S(f = μ · f_0) = s_0 · T · a_μ$. Mit $s_0 = 5 V$ und $T = 0.2 ms$ ⇒ $s_0 · T = 10^{–3} V/Hz$ gilt weiter: $$\mu = 0,\hspace{0.1cm} a_0 = 0 : S (f = 0) \hspace{0.15cm}\underline {= 0},\hspace{8cm}.$$ $$\mu = 1, \hspace{0.1cm}a_1 = +1 : S (f = 5\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= 10^{-3}\,\,{\rm{V/Hz}}},$$ $$\mu = 2, \hspace{0.1cm}a_2 = -1 : S (f = 10\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= -10^{-3}\,\,{\rm{V/Hz}}},$$ $$\mu = 3, \hspace{0.1cm}a_3 = +1 : S (f = 15\,\,{\rm{kHz}}) \hspace{0.15cm}\underline {= 10^{-3}\,\,{\rm{V/Hz}}}.$$

6. Beide Aussagen sind richtig. Die Orthogonalität bezüglich des Frequenzbereichs wurde bereits in der Teilaufgabe e) gezeigt. Die Orthogonalität hinsichtlich des Zeitbereichs ergibt sich aus der Begrenzung der einzelnen Symbole jeweils auf die Zeitdauer T.