Difference between revisions of "Aufgaben:Exercise 1.1Z: Non-redundant Binary Source"
From LNTwww
| Line 7: | Line 7: | ||
Eine jede digitale Quelle kann durch ihre Quellensymbolfolge | Eine jede digitale Quelle kann durch ihre Quellensymbolfolge | ||
$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ | $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ | ||
| − | vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit 0 beginnt. Entstammt jedes einzelne Symbol===Fragebogen=== | + | vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit 0 beginnt. Entstammt jedes einzelne Symbol |
| + | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
Revision as of 21:48, 19 October 2017
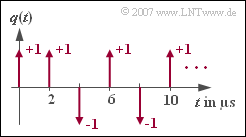
Eine jede digitale Quelle kann durch ihre Quellensymbolfolge $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit 0 beginnt. Entstammt jedes einzelne Symbol
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)