Difference between revisions of "Zusatzaufgaben:1.1 Einfaches Pfadverlustmodell"
From LNTwww
| Line 8: | Line 8: | ||
:$$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$ | :$$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$ | ||
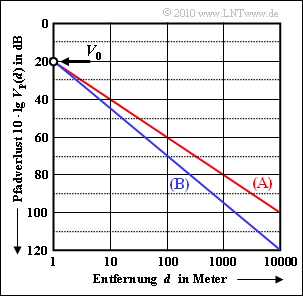
| − | Die Grafik zeigt den Pfadverlust | + | Die Grafik zeigt den Pfadverlust $V_P(d)$ in dB. Auch die Abszisse $d$ ist logarithmisch dargestellt. In obiger Gleichung sind verwendet: |
| − | * die Distanz | + | * die Distanz $d$ von Sender und Empfänger, |
| − | * die Bezugsentfernung | + | * die Bezugsentfernung $d$_0 = 1 m$, |
| − | * der Pfadverlustexponent | + | * der Pfadverlustexponent $\gamma$, |
| − | * die Wellenlänge | + | * die Wellenlänge $\lambda$ der elektromagnetischen Welle. |
| − | Gezeigt sind zwei Szenarien (A) und (B) mit gleichem Pfadverlust bei der Distanz | + | Gezeigt sind zwei Szenarien (A) und (B) mit gleichem Pfadverlust bei der Distanz $d_0 = 1 m$: |
:$$V_{\rm 0} = V_{\rm P}(d = d_0) = 20\,{\rm dB} \hspace{0.05cm}.$$ | :$$V_{\rm 0} = V_{\rm P}(d = d_0) = 20\,{\rm dB} \hspace{0.05cm}.$$ | ||
| − | Eines dieser beiden Szenarien beschreibt die so genannte <i>Freiraumdämpfung</i>, charakterisiert durch den Pfadverlustexponenten | + | Eines dieser beiden Szenarien beschreibt die so genannte <i>Freiraumdämpfung</i>, charakterisiert durch den Pfadverlustexponenten $\gamma = 2$. Die Gleichung für die Freiraumdämpfung gilt allerdings nur im <i>Fernfeld</i>, also wenn der Abstand $d$ zwischen Sender und Empfänger größer ist als die „Fraunhofer–Distanz” |
:$$d_{\rm F} = {2 D^2}/{\lambda} \hspace{0.05cm}.$$ | :$$d_{\rm F} = {2 D^2}/{\lambda} \hspace{0.05cm}.$$ | ||
| − | Hierbei ist | + | Hierbei ist $D$ die größte physikalische Abmessung der Sendeantenne. Bei einer $\lambda/2$ –Antenne erhält man hierfür das einfache Ergebnis: |
:$$d_{\rm F} = \frac{2 \cdot (\lambda/2)^2}{\lambda} = {\lambda}/{2}\hspace{0.05cm}.$$ | :$$d_{\rm F} = \frac{2 \cdot (\lambda/2)^2}{\lambda} = {\lambda}/{2}\hspace{0.05cm}.$$ | ||
| − | '''Hinweis:''' Die Aufgabe gehört zum [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Kapitel 1.1]]. Die Lichtgeschwindigkeit beträgt | + | '''Hinweis:''' Die Aufgabe gehört zum [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Kapitel 1.1]]. Die Lichtgeschwindigkeit beträgt $c = 3 \cdot 10^8 m/s$. |
{{Display}} | {{Display}} | ||
Revision as of 13:36, 22 October 2017
Funkübertragung bei Sichtverbindung lässt sich durch das sog. Pfadverlustmodell beschreiben, das durch folgende Gleichungen gegeben ist:
- $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$
- $$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$
Die Grafik zeigt den Pfadverlust $V_P(d)$ in dB. Auch die Abszisse $d$ ist logarithmisch dargestellt. In obiger Gleichung sind verwendet:
- die Distanz $d$ von Sender und Empfänger,
- die Bezugsentfernung $d$_0 = 1 m$, * der Pfadverlustexponent $\gamma$, * die Wellenlänge $\lambda$ der elektromagnetischen Welle. Gezeigt sind zwei Szenarien (A) und (B) mit gleichem Pfadverlust bei der Distanz $d_0 = 1 m$: :'"`UNIQ-MathJax3-QINU`"' Eines dieser beiden Szenarien beschreibt die so genannte <i>Freiraumdämpfung</i>, charakterisiert durch den Pfadverlustexponenten $\gamma = 2$. Die Gleichung für die Freiraumdämpfung gilt allerdings nur im <i>Fernfeld</i>, also wenn der Abstand $d$ zwischen Sender und Empfänger größer ist als die „Fraunhofer–Distanz” :'"`UNIQ-MathJax4-QINU`"' Hierbei ist $D$ die größte physikalische Abmessung der Sendeantenne. Bei einer $\lambda/2$ –Antenne erhält man hierfür das einfache Ergebnis: :'"`UNIQ-MathJax5-QINU`"' '''Hinweis:''' Die Aufgabe gehört zum [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Kapitel 1.1]]. Die Lichtgeschwindigkeit beträgt $c = 3 \cdot 10^8 m/s$.