Difference between revisions of "Aufgaben:Exercise 3.4: Optimization of the Cutoff Frequency"
| Line 4: | Line 4: | ||
[[File:P_ID1419__Dig_A_3_4.png|right|frame]] | [[File:P_ID1419__Dig_A_3_4.png|right|frame]] | ||
| + | Wir vergleichen ein redundanzfreies Binärsystem ($M = 2$) und ein redundanzfreies Quaternärsystem ($M = 4$) hinsichtlich ihrer S/N–Verhältnisse im ungünstigsten Fall: | ||
| + | :$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei ist $\ddot{o}(T_D)$ die vertikale Augenöffnung und $\sigma_d^2$ gibt die Detektionsrauschleistung an. Für beide Systemkonfigurationen gelten die gleichen Randbedingungen (ähnlich wie in Aufgabe Z3.4): | ||
| + | * Der rechteckige Sendegrundimpuls $g_s(t)$ im NRZ–Format hat die Höhe $s_0 = 1 \, {\rm V}$. | ||
| + | * Die (äquivalente) Bitrate beträgt in beiden Fällen $R_B = 100 \, {\rm Mbit/s}$. | ||
| + | * Der Kanal besteht aus einem Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 80 \, {\rm dB}$ (bzw. $9.2 \, {\rm Np}$). | ||
| + | * Das Empfangsfilter sei ein Gaußtiefpass mit der Grenzfrequenz $f_G$, die zu optimieren ist: | ||
| + | :$$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$ | ||
| + | * Am Kanalausgang liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0$ vor. | ||
| + | * Die Entscheiderschwellen sind optimal gewählt und der Detektionszeitpunkt $T_D = 0$ ebenfalls. | ||
| + | |||
| + | |||
| + | Im Gegensatz zur Aufgabe Z3.4 (feste Grenzfrequenz $f_G = 30 \, {\rm MHz}$) ist hier die Grenzfrequenz des Gaußtiefpasses variable und sie soll so bestimmt werden, dass das ungünstigste S/N–Verhältnis $\rho_U$ maximiert und damit die (ungünstigste) Fehlerwahrscheinlichkeit $p_U$ minimiert wird. | ||
| + | Die Tabelle zeigt die (normierte) halbe Augenöffnung und den (normierten) Detektionsrauscheffektivwert für das Binärsystem ($M = 2$) und das Quaternärsystem ($M = 4$) sowie für verschiedene (normierte) Grenzfrequenzen. Die Normierung basiert dabei auf der Bitrate $R_B$. | ||
| + | Anzumerken ist: | ||
| + | * Die Tabelle gilt für $E_B/N_0 = 5 \cdot 10^8$ und für die charakteristische Kabeldämpfung $a_* = 80 \, {\rm dB}$ (bzw. $9.2 \, {\rm Np}$). | ||
| + | * Die (normierte Rauchleistung ergibt sich unter Berücksichtigung des idealen Kanalentzerrers zu | ||
| + | :$$\frac{ \sigma_d^2}{N_{\rm 0} \cdot R_{\rm B}} = \frac{ 1}{R_{\rm | ||
| + | B}} \cdot \int_{0}^{\infty}{\rm exp}\left [2 \cdot 9.2 | ||
| + | \cdot \sqrt{2 \cdot f/R_{\rm B}} - 2\pi \cdot \frac{(f/R_{\rm | ||
| + | B})^2}{(2 f_{\rm G}/R_{\rm B})^2} \right ]{\rm d} \hspace{0.05cm} f | ||
| + | \hspace{0.05cm}.$$ | ||
| + | * Wie in Aufgabe Z3.4 noch hergeleitet wird, gilt für die (normierte) halbe Augenöffnung: | ||
| + | :$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{1}{ M-1}\cdot \left [1- 2 \cdot M \cdot {\rm Q} \left( | ||
| + | \sqrt{2\pi} \cdot {\rm ld}\hspace{0.1cm}(M) \cdot \frac{f_{\rm | ||
| + | G}}{R_{\rm B}} | ||
| + | \right)\right] | ||
| + | \hspace{0.05cm}.$$ | ||
| + | * Damit kann für das ungünstigste S/N–Verhältnis geschrieben werden: | ||
| + | :$$\rho_{\rm U} = \left [\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \right ]^2 \cdot | ||
| + | \frac{N_{\rm 0} \cdot R_{\rm B}}{ \sigma_d^2} \cdot \frac{ s_0^2}{N_{\rm 0} \cdot R_{\rm B}} | ||
| + | \hspace{0.05cm},$$ | ||
| + | |||
| + | wobei der letzte Term bei dem hier betrachteten NRZ–Rechteckimpuls als "<i>Energie pro Bit bezogen auf die Rauschleistungsdichte</i>" interpretiert werden kann. | ||
| + | Für die Lösung der Aufgabe sind die hier gemachten Anmerkungen nicht relevant. In der Tabelle ist $\sigma_d/s_0$ angegeben, das heißt, dass hier der zweite und der dritte Term obiger Gleichung zusammengefasst sind. Durch Division des jeweils ersten Spaltenelements (normierte halbe Augenöffnung) durch das zweite in der Tabelle angegebene Element ($\sigma_d/s_0$) und Quadrieren des Quotienten kommt man hier sehr einfach zum Ergebnis $\rho_U$. | ||
| + | |||
| + | ''Hinweis:'' Die Aufgabe bezieht sich auf die theoretischen Grundlagen von [[Digitalsignal%C3%BCbertragung/Impulsinterferenzen_bei_mehrstufiger_%C3%9Cbertragung|Kapitel 3.4]]. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 13:05, 24 October 2017
Wir vergleichen ein redundanzfreies Binärsystem ($M = 2$) und ein redundanzfreies Quaternärsystem ($M = 4$) hinsichtlich ihrer S/N–Verhältnisse im ungünstigsten Fall:
- $$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} \hspace{0.05cm}.$$
Hierbei ist $\ddot{o}(T_D)$ die vertikale Augenöffnung und $\sigma_d^2$ gibt die Detektionsrauschleistung an. Für beide Systemkonfigurationen gelten die gleichen Randbedingungen (ähnlich wie in Aufgabe Z3.4):
- Der rechteckige Sendegrundimpuls $g_s(t)$ im NRZ–Format hat die Höhe $s_0 = 1 \, {\rm V}$.
- Die (äquivalente) Bitrate beträgt in beiden Fällen $R_B = 100 \, {\rm Mbit/s}$.
- Der Kanal besteht aus einem Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 80 \, {\rm dB}$ (bzw. $9.2 \, {\rm Np}$).
- Das Empfangsfilter sei ein Gaußtiefpass mit der Grenzfrequenz $f_G$, die zu optimieren ist:
- $$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$
- Am Kanalausgang liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0$ vor.
- Die Entscheiderschwellen sind optimal gewählt und der Detektionszeitpunkt $T_D = 0$ ebenfalls.
Im Gegensatz zur Aufgabe Z3.4 (feste Grenzfrequenz $f_G = 30 \, {\rm MHz}$) ist hier die Grenzfrequenz des Gaußtiefpasses variable und sie soll so bestimmt werden, dass das ungünstigste S/N–Verhältnis $\rho_U$ maximiert und damit die (ungünstigste) Fehlerwahrscheinlichkeit $p_U$ minimiert wird.
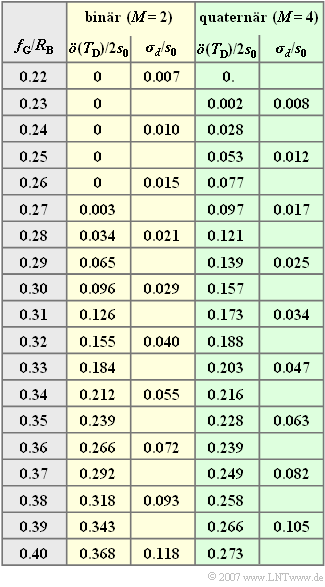
Die Tabelle zeigt die (normierte) halbe Augenöffnung und den (normierten) Detektionsrauscheffektivwert für das Binärsystem ($M = 2$) und das Quaternärsystem ($M = 4$) sowie für verschiedene (normierte) Grenzfrequenzen. Die Normierung basiert dabei auf der Bitrate $R_B$.
Anzumerken ist:
- Die Tabelle gilt für $E_B/N_0 = 5 \cdot 10^8$ und für die charakteristische Kabeldämpfung $a_* = 80 \, {\rm dB}$ (bzw. $9.2 \, {\rm Np}$).
- Die (normierte Rauchleistung ergibt sich unter Berücksichtigung des idealen Kanalentzerrers zu
- $$\frac{ \sigma_d^2}{N_{\rm 0} \cdot R_{\rm B}} = \frac{ 1}{R_{\rm B}} \cdot \int_{0}^{\infty}{\rm exp}\left [2 \cdot 9.2 \cdot \sqrt{2 \cdot f/R_{\rm B}} - 2\pi \cdot \frac{(f/R_{\rm B})^2}{(2 f_{\rm G}/R_{\rm B})^2} \right ]{\rm d} \hspace{0.05cm} f \hspace{0.05cm}.$$
- Wie in Aufgabe Z3.4 noch hergeleitet wird, gilt für die (normierte) halbe Augenöffnung:
- $$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{1}{ M-1}\cdot \left [1- 2 \cdot M \cdot {\rm Q} \left( \sqrt{2\pi} \cdot {\rm ld}\hspace{0.1cm}(M) \cdot \frac{f_{\rm G}}{R_{\rm B}} \right)\right] \hspace{0.05cm}.$$
- Damit kann für das ungünstigste S/N–Verhältnis geschrieben werden:
- $$\rho_{\rm U} = \left [\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \right ]^2 \cdot \frac{N_{\rm 0} \cdot R_{\rm B}}{ \sigma_d^2} \cdot \frac{ s_0^2}{N_{\rm 0} \cdot R_{\rm B}} \hspace{0.05cm},$$
wobei der letzte Term bei dem hier betrachteten NRZ–Rechteckimpuls als "Energie pro Bit bezogen auf die Rauschleistungsdichte" interpretiert werden kann. Für die Lösung der Aufgabe sind die hier gemachten Anmerkungen nicht relevant. In der Tabelle ist $\sigma_d/s_0$ angegeben, das heißt, dass hier der zweite und der dritte Term obiger Gleichung zusammengefasst sind. Durch Division des jeweils ersten Spaltenelements (normierte halbe Augenöffnung) durch das zweite in der Tabelle angegebene Element ($\sigma_d/s_0$) und Quadrieren des Quotienten kommt man hier sehr einfach zum Ergebnis $\rho_U$.
Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.4.
Fragebogen
Musterlösung