Aufgaben:Exercise 3.4Z: Eye Opening and Level Number

• Return to book

In dieser Aufgabe werden ein redundanzfreies Binärsystem und ein redundanzfreies Quaternärsystem hinsichtlich vertikaler Augenöffnung miteinander verglichen. Für die beiden Übertragungssysteme gelten die gleichen Randbedingungen:

• Der Sendegrundimpuls $g_s(t)$ ist jeweils NRZ–rechteckförmig und besitze die Höhe $s_0 = 1 \, {\rm V}$.
• Die (äquivalente) Bitrate beträgt $R_B = 100 \, {\rm Mbit/s}$.
• Das AWGN–Rauschen besitzt die Rauschleisungsdichte $N_0$.
• Das Empfangsfilter sei ein Gaußtiefpass mit der Grenzfrequenz $f_G = 30 \, {\rm MHz}$:

$$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$

• Die Entscheiderschwellen sind optimal. Der Detektionszeitpunkt ist $T_D = 0$.

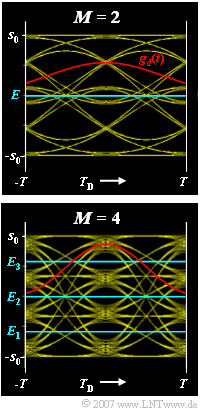
Für die halbe Augenöffnung eines $M$–stufigen Übertragungssystems gilt allgemein:

$${\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_\nu | - \sum_{\nu = 1}^{\infty} |g_{-\nu} |\hspace{0.05cm}.$$

Hierbei ist $g_0 = g_d(t = 0)$ der Hauptwert des Detektionsgrundimpulses $g_d(t) = g_s(t) * h_G(t)$. Der zweite Term beschreibt die Nachläufer $g_{\rm \nu} = g_d(t = \nu T)$ und der letzte Term die Vorläufer $g_{\rm -\nu} = g_d(t = -\nu T)$. Beachten Sie, dass bei der vorliegenden Konfiguration mit Gaußtiefpass

• alle Detektionsgrundimpulswerte $... \, g_{\rm -1}, \, g_0, \, g_1, \, ...$ positiv sind,
• die Summe $... \, + \, g_{\rm -1} + g_0 + g_1\,...$ den konstanten Wert $s_0$ ergibt,
• der Hauptwert mit der komplementären Gaußschen Fehlerfunktion $Q(x)$ berechnet werden kann:

$$g_0 = s_0 \cdot\left [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right] \hspace{0.05cm}.$$

Die Grafik zeigt die Augendiagramme des Binär– und des Quaternärsystems sowie – in roter Farbe – die zugehörigen Detektionsgrundimpulse $g_d(t)$. Eingezeichnet sind auch die optimalen Entscheiderschwellen $E$ (für $M = 2$) bzw. $E_1$, $E_2$, $E_3$ (für $M = 4$). In der Aufgabe g) sollen diese numerisch ermittelt werden.

Hinweis: Die Aufgabe gehört zu Kapitel 3.4. Für die komplementäre Gaußsche Fehlerfunktion gilt:

$${\rm Q}(0.25) = 0.4013,\hspace{0.2cm}{\rm Q}(0.50) = 0.3085,\hspace{0.2cm}{\rm Q}(0.75) = 0.2266,\hspace{0.2cm}{\rm Q}(1.00) = 0.1587,$$

$${\rm Q}(1.25) = 0.1057,\hspace{0.2cm}{\rm Q}(1.50) = 0.0668,\hspace{0.2cm}{\rm Q}(1.75) = 0.0401,\hspace{0.2cm}{\rm Q}(2.00) = 0.0228.$$

Fragebogen

1

Wie groß sind die Symboldauern beim Binär– und beim Quaternärsystem?

$M = 2: T$ = ${\rm ns}$

$M = 4: T$ = ${\rm ns}$

2

Berechnen Sie den Hauptwert für das Binärsystem.

$M = 2: g_0$ = ${\rm V}$

3

Berechnen Sie den Hauptwert für das Quaternärsystem.

$M = 4: g_0$ = ${\rm V}$

4

Welche Gleichungen gelten unter Berücksichtigung des Gaußtiefpasses?

	$\ddot{o}(T_D)/2 = M \cdot g_0/(M – 1) – s_0,$
	$\ddot{o}(T_D)/2 = M \cdot s_0/(M – 1) – g_0,$
	$\ddot{o}(T_D)/2 = s_0/(M – 1) \cdot [1 – 2 \cdot M \cdot Q(2\pi)^{\rm 1/2} \cdot {\rm log_2} \, (M) \cdot f_G/R_B)].

5

Welche Augenöffnung ergibt sich für das Binärsystem?

$M = 2: \ddot{o}(T_D)$ = $V$

6

Welche Augenöffnung ergibt sich für das Quaternärsystem?

$M = 4: \ddot{o}(T_D)$ = $V$

7

Bestimmen Sie die optimalen Schwellenwerte des Quaternärsystems. Geben Sie zur Kontrolle den Schwellenwert $E_1$ ein.

$M = 4: E_1$ =

Musterlösung

Solution

(1) (2) (3) (4) (5)