Difference between revisions of "Aufgaben:Exercise 3.5: Eye Opening with Pseudoternary Coding"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Impulsinterferenzen_bei_mehrstufiger_Übertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=sim…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1421__Dig_A_3_5.png|right|frame]] |
| + | Betrachtet werden drei Nachrichtenübertragungssysteme, jeweils mit folgenden übereinstimmenden Eigenschaften: | ||
| + | * NRZ–Rechteckimpulse mit der Amplitude $s_0 = 2 \, {\rm V}$, | ||
| + | * Koaxialkabel mit charakteristischer Kabeldämpfung $a_* = 40 \, {\rm dB}$, | ||
| + | * AWGN–Rauschen mit der Rauschleistungsdichte $N_0$, | ||
| + | * Empfangsfilter, bestehend aus einem idealen Kanalentzerrer und einem Gaußtiefpass mit der normierten Grenzfrequenz $f_G \cdot T \approx 0.5$. | ||
| + | * Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt $T_D = 0$. | ||
| + | |||
| + | |||
| + | Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes: | ||
| + | <font color="#cc0000"><span style="font-weight: bold;">System A</span></font> verwendet ein binäres bipolares redundanzfreies Sendesignal. Von diesem System sind folgende Beschreibungsgrößen bekannt: | ||
| + | * Grundimpulswerte $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, ... \, \approx 0$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} | ||
| + | -g_{1}-g_{-1} = 1.12\,{\rm V} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | * Rauscheffektivwert $\sigma_d \approx = 0.2 \, {\rm V} | ||
| + | :$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ | ||
| + | \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
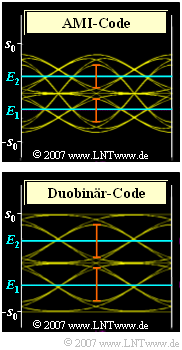
| + | <font color="#cc0000"><span style="font-weight: bold;">System B</span></font> verwendet AMI–Codierung. Hier treten die äußeren Symbole $"+1"$ bzw, $"–1"$ nur isoliert auf. Bei drei aufeinanderfolgenden Symbolen sind unter Anderem die zwei Folgen $" \, ... \, , \, +1, \, +1, \, +1, \, ... \,"$ und $" \, ... \, , \, +1, \, 0, \, +1, \, ..." nicht möglich im Gegensatz zu $" \, ... \, , \, +1, \, –1, \, +1, \, ... \,"$ | ||
| + | <font color="#cc0000"><span style="font-weight: bold;">System C</span></font> verwendet Duobinärcode. Hier wird die alternierende Folge $" \, ... \, , \, –1, \, +1, \, –1, \, ... \,"$ durch den Code ausgeschlossen, was sich günstig auf die Augenöffnung auswirkt. | ||
| + | |||
| + | ''Hinweis:'' Diese Aufgabe bezieht sich auf das [[Digitalsignal%C3%BCbertragung/Impulsinterferenzen_bei_mehrstufiger_%C3%9Cbertragung|Kapitel 3.4]]. Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich. | ||
| Line 28: | Line 52: | ||
| − | [[Category:Aufgaben zu Digitalsignalübertragung|^3. | + | [[Category:Aufgaben zu Digitalsignalübertragung|^3.4 Augendiagramm mehrstufiger Systeme^]] |
Revision as of 12:47, 25 October 2017
Betrachtet werden drei Nachrichtenübertragungssysteme, jeweils mit folgenden übereinstimmenden Eigenschaften:
- NRZ–Rechteckimpulse mit der Amplitude $s_0 = 2 \, {\rm V}$,
- Koaxialkabel mit charakteristischer Kabeldämpfung $a_* = 40 \, {\rm dB}$,
- AWGN–Rauschen mit der Rauschleistungsdichte $N_0$,
- Empfangsfilter, bestehend aus einem idealen Kanalentzerrer und einem Gaußtiefpass mit der normierten Grenzfrequenz $f_G \cdot T \approx 0.5$.
- Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt $T_D = 0$.
Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes:
System A verwendet ein binäres bipolares redundanzfreies Sendesignal. Von diesem System sind folgende Beschreibungsgrößen bekannt:
- Grundimpulswerte $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, ... \, \approx 0$
- $$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} -g_{1}-g_{-1} = 1.12\,{\rm V} \hspace{0.05cm}.$$
- Rauscheffektivwert $\sigma_d \approx = 0.2 \, {\rm V} :'"`UNIQ-MathJax4-QINU`"' <font color="#cc0000"><span style="font-weight: bold;">System B</span></font> verwendet AMI–Codierung. Hier treten die äußeren Symbole $"+1"$ bzw, $"–1"$ nur isoliert auf. Bei drei aufeinanderfolgenden Symbolen sind unter Anderem die zwei Folgen $" \, ... \, , \, +1, \, +1, \, +1, \, ... \,"$ und $" \, ... \, , \, +1, \, 0, \, +1, \, ..." nicht möglich im Gegensatz zu $" \, ... \, , \, +1, \, –1, \, +1, \, ... \,"$
System C verwendet Duobinärcode. Hier wird die alternierende Folge $" \, ... \, , \, –1, \, +1, \, –1, \, ... \,"$ durch den Code ausgeschlossen, was sich günstig auf die Augenöffnung auswirkt.
Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 3.4. Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)